|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Стратегии обучения и самообучения
Пусть в процессе эксплуатации обученной сети выяснилось, что ситуации (эталоны) А1&B1&C1 и A1&B1&C3, в дополнение к ранее предусмотренным, не только возможны, но требуют того же решения R1. Это означает, что обобщенный эталон A1&B1&C2&C4 мы должны расширить до подобного эталона A1&B1&С1&C2&C3&C4, требующего решения R1. То есть нам необходимо построить путь возбуждения (трассы) B1, A1, C1, C2, C3, C4 -> Вых1. Однако при его построении мы не хотим изменять уже ранее построенный путь возбуждения B1, A1, C2, C4 -> Вых1.
Значит, надо проложить трассы, дополнить сеть путем возбуждения C1, C3 -> Вых1. При этом нам бы хотелось максимально объединить, пересечь, слить этот путь с уже построенным ранее путем возбуждения, ведущим в Вых1.
Преследуя эту цель, мы не должны допустить слияния, влияния этого пути на пути возбуждения, ведущие в другие нейроны выходного слоя. Такая опасность кроется в естественном желании переиспользования нейронов. Ведь слияние двух путей возбуждения заключается в том, что у некоторых нейронов следует повысить веса синапсических связей (скажем, положить равным единице, вместо нуля, окрасить в красный цвет). То есть некоторые нейроны могут стать преемниками возбуждения большего, чем прежде, числа нейронов. А если эти нейроны использовались для получения других решений?
Здесь важно сделать Замечание в дополнение к алгоритму трассировки, рассмотренному в "Трассировка нейронной сети" :
целесообразно при переиспользовании нейронов, возникающем при последовательном анализе обобщенных эталонов , фиксировать информацию: участвует ли данный нейрон лишь в одном пути возбуждения - к единственному нейрону выходного слоя и к какому именно, или к более чем к одному нейрону выходного слоя. И этого будет вполне достаточно для ликвидации тревог.
Продолжим рассмотрение примера, ведущее к обобщению.
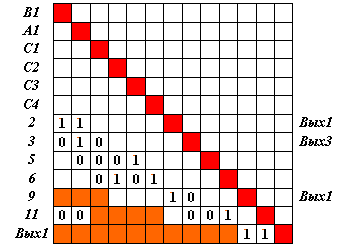
Для нового обобщенного эталона на основе матрицы S, так же, как мы это делали в предыдущем разделе, построим (рис. 5.3) матрицу S*[B1, A1, C1, C2, C3, C4 -> Вых1].
В соответствии с правилом ее построения в ней представлены лишь те нейроны, для которых число единиц в строке равно соответствующему значению m. Для каждой строки, содержащей единичные элементы, указано, используется ли нейрон для получения единственного решения и какого (признак Выхi ), или не единственного (признак отсутствует).
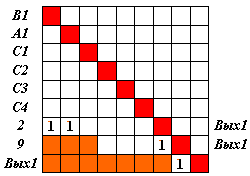
Исключим из построенной матрицы строки и столбцы, соответствующие нейронам, участвующим в путях возбуждения, не ведущих в Вых1 (рис. 5.4). (В общем случае в матрице могли сохраниться строки, содержащие нулевые веса.)
"Спускаемся" по столбцу, соответствующему нейрону С1, и в строке, не являющейся входом, находим, если таковой имеется, первый нулевой элемент. Полагаем его равным единице и отражаем введенное изменение в матрице S. Если нулевого элемента в столбце не нашлось, находим первый "пустой" элемент (или отмеченный транзитивной связью - все равно) и полагаем его равным единице. Этим мы вводим дополнительную связь, отраженную в матрице S. В данном случае такой связью с единичным весом является связь С1 -> 2.
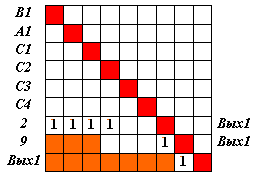
То же проделываем с нейроном С3, введя дополнительную связь с единичным весом С3 -> 2 (рис. 5.5).
Отметим, что наше решение основано на эвристике, и место появления новых возбужденных связей может быть оспорено. Например, могли быть построены связи С1-> 2, С3 -> 9, или С1-> Вых1, С3 -> 9, или С1-> 9, С3-> Вых1, и т.д.
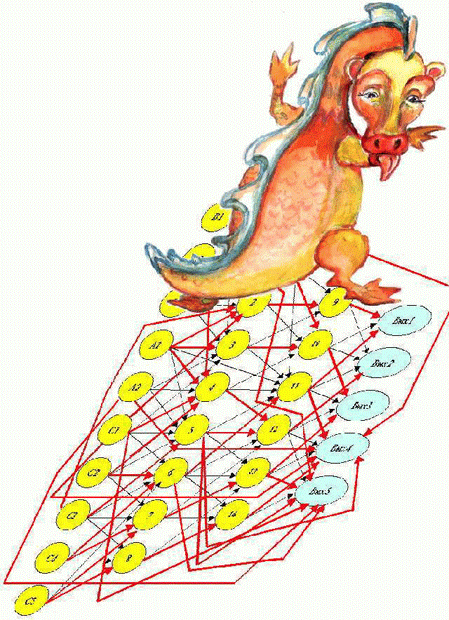
Мы не приводим еще более усложнившегося рис. 5.1 уточненной сети, предоставив читателю возможность проверить усвоение материала с помощью легкого нажатия красным карандашом прямо в книжке в направлении стрелок, которые исходят из кружочков, помеченных символами С1 и С3, и входят в кружок, помеченный цифрой 2. Однако намек на такое уточнение делаем на рис. 5.6.