НОУ ИНТУИТ | Исследование операций и модели экономического поведения. Лекция 3: Устойчивость и эффективность поведения сторон: принцип максимума гарантированного результата

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Нижегородский государственный университет им. Н.И.Лобачевского

Опубликован: 26.04.2007 | Доступ: свободный | Студентов: 1415 / 126 | Оценка: 3.69 / 3.54 | Длительность: 14:45:00

ISBN: 978-5-9556-0072-7

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Замечание 1.8 (о прогнозных оценках, реализующихся в ходе операции). Отмеченное совпадение интересов сторон при прогнозировании последствий выбора на основе оценок худшего случая не меняет факта (1.21) равенства нулю суммы их критериев в момент проведения конкурса. Дело в том, что худшая оценка (2.5}, прогнозируемая стороной P₁, например, для случая x₁>x₂ соответствует проведению конкурса в момент $t_{1}^{*} =0$ . Что же касается худшей оценки (2.8)}, прогнозируемой стороной P₂ при том же условии x₁>x₂, то ей соответствует момент $t_{2}^{*} =2$ . Рассмотренную ситуацию иллюстрирует рис. 1.3.

Рис. 1.3.

Таким образом, худшие опасения сторон не могут реализоваться одновременно. Если конкурс произойдет, например, в момент t=0, то при выполнении условий x₁>x₂, эффективность стороны P₁ действительно характеризуется величиной (2.5). Однако реализующаяся при этом оценка

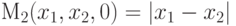
$\text{M}_2(x_1,x_2,0)=|x_1-x_2|$

для стороны P_2 существенно превышает величину (2.8) поскольку момент t=0 проведения конкурса не совпадает со сроком $t_{2}^{*} =2$ , определяющим наступление худшего случая.

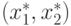Совпадение интересов сторон при ориентации выбора стратегий на достижение максимального гарантированного результата позволяет им вступить в кооперацию и договориться о выборе некоторого одинакового уровня инвестиций $\alpha$ , который задает стратегическую пару $(x_{1}^{*},x_{2}^{*})$ , удовлетворяющую условию

$x_1^*=x_2^*=\alpha,\quad \alpha\in [0,1],$

( 2.11)

и обеспечивающую каждой из сторон максимальную оценку

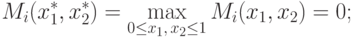$M_i(x_1^*,x_2^*)=\max_{0\le x_1,\, x_2\le 1}M_i(x_1,x_2)=0;$

( 2.12)

ср. с правым неравенством в (2.10).

Правила конкурса предполагают, что уровень качества, обеспечиваемый участниками, в любом случае должен быть не ниже, чем заданный порог W_min, где $0\le W_{\min}\le 1$ . Поэтому, учитывая (1.19) и (2.11}, получаем, что совместно выбираемый сторонами P₁ и P₂ уровень инвестиций $\alpha$ должен удовлетворять условиям

$\min_{0\le t \le 2}W_i(x_i^*,t)=\min_{0\le t\le 2}[\alpha (t-1)+1]\ge W_{\min},\quad i=1,2.$

Следовательно, параметр $\alpha$ должен удовлетворять неравенствам

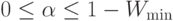$0\le \alpha \le 1-W_{\min}$

( 2.13)

Замечание 1.9 (о лексикографически упорядоченных критериях ). Выбор сторон, отвечающий условиям (2.11}, (2.13} и максимизирующий гарантированные сторонам (одинаковые) уровни эффективности, приводит к ситуации, когда конкурсная комиссия не сможет назвать победителя. В этом случае сторонам, в соответствии с правилами проведения конкурса, будет предложено реализовать подряд совместно. Однако, как следует из (2.11), (2.13), полученное решение является не единственным, если справедливо неравенство W_min<1. В связи с этим, стороны могут использовать остающийся выбор для улучшения показателей своей деятельности. Фактически, рассмотрение этих дополнительных возможностей представляет собой определенное расширение исходной модели.

Например, стороны могут договориться об экономии средств за счет сокращения инвестиций в новые технологии. Решение, отвечающее этому дополнительному требованию, определяется условием 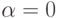$\alpha=0$ , которое совместимо с неравенствами (2.13). Введенный новый критерий можно дополнить условием достижения заданного уровня качества $W_{\max}\ge 1$ к концу периода [0,2]. Такое требование может быть следствием согласованных планов сторон на будущее. Этому дополнительному условию удовлетворяет значение

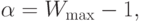$\alpha=W_{\max}-1,$

( 2.14)

которое, в случае справедливости неравенства

$W_{\min}+W_{\max}\le 2,$

( 2.15)

совместимо с (2.13). Графики на рис.1.4 представляют показатели качества сторон, которые соответствуют решениям вида (2.11), удовлетворяющим дополнительным условиям (2.13), (2.14) в предположении справедливости неравенства (2.15).

Рис. 1.4.

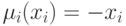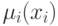Проведенное рассмотрение, как уже отмечено, дополняет критерий M_i(x₁,x₂) стороны P_i, i=1,2, максимум которого достигается на множестве решений, удовлетворяющих условиям (2.11), вторым критерием. Этот второй критерий, отражающий необходимость экономии ресурса, можно формально задать как $\mu_i(x_i)=-x_i$ и считать определенным лишь на указанном выше множестве (т.е. при x₁=x₂. Вводимое при этом дополнительное требование состоит в максимизации $\mu_i(x_i)$ при условии $\alpha\ge W_{\max}-1$ . Таким образом, в результате расширения модели задача выбора для стороны P_i включает два критерия, упорядоченных по важности (или, как говорят, лексикографически упорядоченных. Еще раз отметим, что указанное упорядочение предполагает максимизацию второго критерия на множестве стратегий, обеспечивающих максимизацию первого критерия.

Дальше >>

Авторизоваться

Исследование операций и модели экономического поведения

Устойчивость и эффективность поведения сторон: принцип максимума гарантированного результата

Вопросы и ответы