|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Лекция 9: Алгоритм Дейкстра поиска кратчайших путей в графе
Вторая итерация
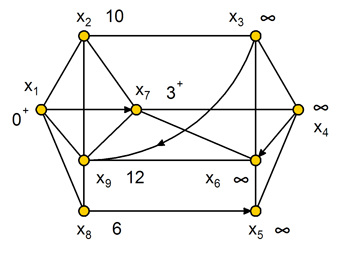
Граф с текущими значениями меток вершин показан на рис. 9.3
Ш А Г 2. Находим Г(х7) = { х2, х4, х6, х9}. Метки всех вершин временные, следовательно пересчитываем их значения:
L(х2)= min [10, 3 + 2 ] = 5,
![L(х_{4})= min [ \infty , 3 + 4 ] = 7](/sites/default/files/tex_cache/1f4c2e848169b8455136235b568060a7.png) ,
,
![L(х_{6})= min [ \infty , 3 + 14 ] = 17](/sites/default/files/tex_cache/92124c9e3c0b31e4862fa10d3a7dc55b.png) ,
,
L(х9)= min [ 12, 3 + 24 ] = 12.
Ш А Г 3. На данном шаге итерации имеем следующие временные метки вершин:
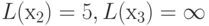 ,
,
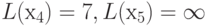 ,
,
L(х6) = 17, L(х8) = 6, L(х9) = 12.
Очевидно, что минимальную метку, равную 5, имеет вершина х2 .
Ш А Г 4. За следующую текущую метку принимаем вершину х2 , т. е. p = х2 , а ее метка становится постоянной, L(х2) = 5+ .
Ш А Г 5. Так как не все вершины графа имеют постоянные метки, переходим к шагу 2.
Третья итерация
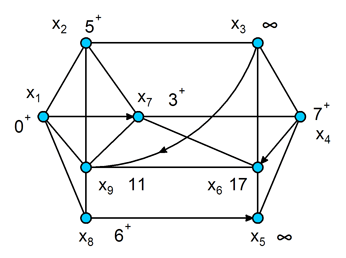
Граф с текущими значениями меток вершин показан на рис. 9.4.
Ш А Г 2. Находим Г(х2) = {х1, х3, х7, х9}. Метки вершин х3 и х9 временные, следовательно пересчитываем их значения:
![L(х_{3}) = min [ \infty , 5 + 18 ] = 23](/sites/default/files/tex_cache/15c3e890cc8f25b6f9ded64422ec897f.png) ,
,
L(х9) = min [ 12, 5+13 ] = 12.
Ш А Г 3. На данном шаге итерации имеем следующие временные метки вершин:
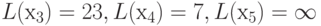 ,
,
L(х6) = 17, L(х8) = 6, L(х9) = 12.
Очевидно, что минимальную метку, равную 6, имеет вершина х8 .
Ш А Г 4. За следующую текущую метку принимаем вершину х8 , т. е. p = х8 , а ее метка становится постоянной, L(х8) = 6+ .
Ш А Г 5. Не все вершины графа имеют постоянные метки, поэтому переходим к шагу 2.
Четвертая итерация
Ш А Г 2. Находим Г(х8) = { х1, х5, х6, х9 }. Метки вершин х5, х6 и х9 временные, следовательно, пересчитываем их значения:
![L(х_{5}) = min [ \infty , 6 + 23 ] = 29](/sites/default/files/tex_cache/fcc3b3ef842b16a71bc25204ae306f1e.png) ,
,
L(х6) = min [ 17, 6 + 15 ] = 17,
L(х9) = min [ 12, 6 + 5 ] = 11.
Ш А Г 3. На данном шаге итерации имеем следующие временные метки вершин:
L(х3) = 23, L(х4) = 7,
L(х5) = 29, L(х6) = 17, L(х9) = 11.
Очевидно, что минимальную метку, равную 7 имеет вершина х4 .
Ш А Г 4. За следующую текущую метку принимаем вершину х4 , т. е. p = х4 , а ее метка становится постоянной, L(х4) = 7+ .
Ш А Г 5. Так как не все вершины графа имеют постоянные метки, переходим к шагу 2.