|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Объединяемые приоритетные очереди
Операции с левосторонними кучами
Операция СЛИЯНИЕ. Эта
операция позволяет слить две левосторонние
кучи 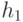 и
и  в одну кучу
в одну кучу  .
Реализуется она посредством
слияния правых путей двух исходных куч в один правый путь, упорядоченный
по правилам кучи, а левые поддеревья узлов сливаемых правых путей остаются
левыми поддеревьями соответствующих узлов в результирующем пути.
В полученной куче необходимо восстановить свойство левизны каждого узла.
Это свойство может быть нарушено только у узлов правого пути полученной кучи,
так как левые поддеревья с корнями в узлах правых путей исходных куч не
изменились. Восстанавливается свойство левизны при помощи прохода правого
пути снизу вверх (от листа к корню) с попутным транспонированием в случае
необходимости левых и правых поддеревьев и вычислением новых рангов
проходимых узлов.
.
Реализуется она посредством
слияния правых путей двух исходных куч в один правый путь, упорядоченный
по правилам кучи, а левые поддеревья узлов сливаемых правых путей остаются
левыми поддеревьями соответствующих узлов в результирующем пути.
В полученной куче необходимо восстановить свойство левизны каждого узла.
Это свойство может быть нарушено только у узлов правого пути полученной кучи,
так как левые поддеревья с корнями в узлах правых путей исходных куч не
изменились. Восстанавливается свойство левизны при помощи прохода правого
пути снизу вверх (от листа к корню) с попутным транспонированием в случае
необходимости левых и правых поддеревьев и вычислением новых рангов
проходимых узлов.
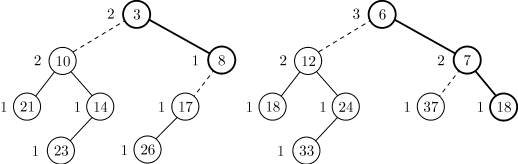
Рассмотрим процесс слияния двух левосторонних куч 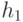 и
и  ,
изображенных на рис. 5.2.
,
изображенных на рис. 5.2.
Числа внутри кружочков являются ключами элементов, приписанных к соответствующим узлам. Правые ветви куч показаны жирными линиями. Числа рядом с узлами — их ранги.
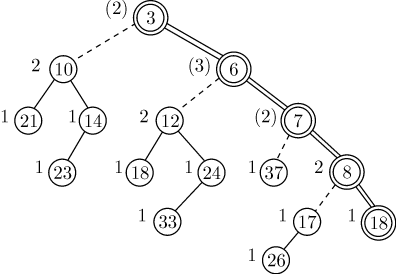
После объединения правых путей получим дерево, изображенное на рис. 5.3. Оно не является левосторонним. В скобках указаны ранги узлов, какими они были в исходных кучах до слияния.
Восстановление свойства левизны кучи начинаем с последнего узла правой
ветви. Это узел с ключом 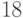 . Очевидно, он должен иметь
ранг
. Очевидно, он должен иметь
ранг  , совпадающий
с его старым значением и поэтому не требующий обновления.
, совпадающий
с его старым значением и поэтому не требующий обновления.
Следующий по направлению к корню узел правой ветви имеет
ключ  , ранг его
левого сына не меньше ранга правого сына, следовательно, условие левизны
выполняется и поэтому транспонирования его левого и правого поддеревьев не
требуется. Однако ранг этого узла необходимо обновить, так как его старое
значение
, ранг его
левого сына не меньше ранга правого сына, следовательно, условие левизны
выполняется и поэтому транспонирования его левого и правого поддеревьев не
требуется. Однако ранг этого узла необходимо обновить, так как его старое
значение  не совпадает с увеличенным на
не совпадает с увеличенным на  минимальным из рангов его
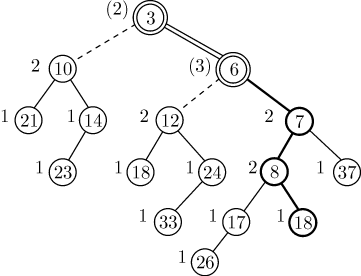
потомков, то есть с числом 2. Обновив ранг, получим кучу, изображенную на
рис. 5.4.
минимальным из рангов его
потомков, то есть с числом 2. Обновив ранг, получим кучу, изображенную на
рис. 5.4.
Теперь рассмотрим узел с ключом 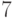 . Он имеет левого сына с
ключом
. Он имеет левого сына с
ключом 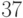 и рангом
и рангом  и правого сына с ключом
и правого сына с ключом  и
рангом
и
рангом 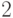 . Для восстановления свойства
левизны в этом узле необходимо поменять местами его левое и правое
поддеревья и обновить ранг. Его новым значением будет минимум из рангов
его потомков (это ранг нового правого сына) плюс
. Для восстановления свойства
левизны в этом узле необходимо поменять местами его левое и правое
поддеревья и обновить ранг. Его новым значением будет минимум из рангов
его потомков (это ранг нового правого сына) плюс  , то
есть
, то
есть 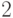 .
В результате получаем дерево, изображенное на рис. 5.5.
.
В результате получаем дерево, изображенное на рис. 5.5.