| Россия |
Моделирование дедуктивного и индуктивного мышления с помощью языка логического вывода ПРОЛОГ
...Вот вы упомянули сейчас умение наблюдать и умение делать выводы. А мне казалось, что это – почти одно и то же.
- Нет, это разные вещи, ответил Шерлок Холмс... Отбросьте всё, что не могло иметь место, и останется один-единственный факт, который и есть истина.
А. Конан Дойл. Записки о Шерлоке Холмсе
О языке логического программирования ПРОЛОГ
Идея использования математической логики в качестве языка программирования возникла впервые в начале 70-х годов. Первыми исследователями были Роберт Ковальский из Эдинбурга (теоретические аспекты), Маартен Ван Эмден из Эдинбурга (экспериментальная демонстрационная система) и Ален Колмероэ из Марселя (реализация). Сегодняшней своей популярности ПРОЛОГ во многом обязан эффективной реализации этого языка, полученной в Эдинбурге Дэвидом Уорреном в середине 70-х годов.
Пролог представляет собой базу знаний как совокупность фактов и правил (вывода). Факты и правила по смыслу группируются в процедуры, имеющие имя. Процедурная структура позволяет включать (в правила) конструкции любых других алгоритмических языков. То есть, ПРОЛОГ является логической надстройкой, сублимирующей лишь операции логического вывода.
Формируется цель логического вывода, и если она не противоречива, выявляются факты, из которых эта цель следует.
Например, цель может иметь вид: дядя(X, Y). Её решение (вывод) заключается в нахождении всех пар переменных (имён объектов) X и Y, для которых истинно утверждение "Х является дядей Y".
Для решения такой задачи используется приём трансформации цели, где цель на основе рекурсии правил представляется дедуктивной цепочкой – сложной целью, в которой фигурируют переменные. Перебираются все варианты связывания переменных, т.е. придания им возможных значений на основе фактов. Каждый вариант связывания переменных проверяется на непротиворечивость. Процедура такой проверки называется унификацией. Вариант полного связывания всех переменных, прошедший унификацию, определяет решение. Последовательное, пошаговое связывание переменных в случае неудачи (не проходит унификация) или при поиске всех решений, естественно приводит к возврату на предыдущий шаг для испытания другой возможности.
Стратегия такого поступательно-возвратного связывания переменных называется бэктрекингом (backtracking).
Для учебных целей с примерами и задачами язык ПРОЛОГ хорошо описан в [25].
Достаточные сведения читатель получит из последующего текста.
Возможность решения задач логического вывода с помощью языка ПРОЛОГ
Из чего следует исходить, приступая к моделированию индуктивного мышления?
1. Наука призвана открывать новые (не известные ранее) законы природы – законы взаимодействия объектов и явлений.
2. "Наука начинается тогда, когда начинают считать", - сказал Д.И. Менделеев. Действительно, вглядываясь в достижения мировых учёных, обнаруживаем важный факт статистического обеспечения экспериментов и выводов. Сколько раз, по известной легенде, должно было упасть яблоко на голову И. Ньютона, чтобы он сформулировал гипотезу: F = ma? (Ведь для подтверждения гениальной догадки яблоки должны были падать и падать!)
3. Значит, кроме статистической обработки опыта, наука питается логической выводимостью новых знаний. В "простейшем" случае - это математические теоремы. На основе каких статистических оценок Д. Буль мог создать "булеву алгебру"? Да и И. Ньютон, если верить легенде, мог сделать свой вывод на основе измерения получаемой (его головой) энергии W = mgh. Затем, в результате аналитических выкладок, он смог перейти к столь важному основополагающему заключению. Даже в наши дни появляются факты, подтверждающие математически выведенные гипотезы большой давности.
Кстати, а почему F равно ma, а не, скажем, ma2? Ведь на основе такого предположения, такой аксиоматики, вполне можно построить некоторый мир. Физики - математики это знают, препарируя вдоль и поперёк второй закон механики для вывода новых знаний (учеников) о нашем мире. А по законам диалектики Гегеля всё действительное логично (логически выводимо) , а всё логически выводимое – действительно! Это что, - вопрос о параллельных мирах?
Пытаясь расширить действие второго закона механики, мы можем высказать смелую гипотезу:
В Мире Божием действует закон F = maR, где R – действительное, принимающее значение от 0 до 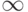 .
.
Мы сможем это проверить сегодня экспериментально? Но ведь возможно, что более развитые существа научились осуществлять дрейф по данному показателю степени, и нечёткие НЛО, внезапно появляющиеся и исчезающие, это демонстрируют (если это не искусный обман).
Таким образом, мы наблюдаем неразрывную связь между дедуктивным и индуктивным мышлением, опирающуюся на многообразие законов природы. Однако важно осознать приоритет: индуктивное мышление строится на основе дедуктивного и далее питает его.
Если моделирование дедуктивного мышления изучено достаточно и является основной целью данного языка, то модель индуктивного мышления, то есть, формирования новых знаний в рамках языка ПРОЛОГ, предлагается впервые. Суть её в следующем. По базе знаний строятся все возможные дедуктивные цепочки логического вывода, следующие из фактов на основе применения правил. Во всём множестве таких цепочек обнаруживаются и выделяются законченные, желательно, повторяющиеся конструкции. Связанные переменные заменяются их абстрактным представлением для формирования обобщённого вида выделенной конструкции. Так создаются гипотезы об описании новых понятий. Этим гипотетическим понятиям присваиваются имена, и они становятся новыми правилами, дополняющими базу знаний. Одновременно описание новых правил дополняет понятийную логическую нейронную сеть для возможности работы с нечёткими данными. Практика успешного, непротиворечивого применения новых правил должна утвердить их высокую достоверность.
В соответствии с высказанной выше идеей, конкретизируем основополагающие парадигмы ИИ для решения наших задач с помощью языка ПРОЛОГ.
-
Парадигма эксперта обретает следующие особенности:
а) Формализация знаний и б) Формирование базы знаний (БЗ) реализуются в результате описания фактов и правил на языке ПРОЛОГ для конкретной изучаемой системы.
в) Дедукция осуществляется методом подстановки в развиваемую конструкцию на основе правил. Однако если поставлена цель, то она достигается (доказывается) методом "бэктрекинга", как рассматривалось выше.
-
Парадигма ученика предполагает действия:
а) Обработка фактов, наблюдений и опыта кроются в уже поставленной задаче в виде фактов и правил, действующих в изучаемой системе.
б) Индуктивное обучение обеспечивается представлением в ПРОЛОГЕ фактов и правил, обусловленных изучаемой системой. Новые знания формируются путём вскрытия одинаковых языковых конструкций в записях различных логических цепочек, следующих из фактов и формируемых на основе правил. Эти конструкции могут быть обобщены и выделены в качестве новых понятий (правил) и обретают имя.
в) Дедукция предполагает правильный вывод с учётом расширенного набора правил в результате индуктивного обучения.

