|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы с открытыми ключами
Концепция криптографии с открытым ключом была предложена Уитфилдом Диффи (Whitfield Diffie) и Мартином Хеллманом (Martin Hellman), и, независимо от них, Ральфом Мерклом (Ralph Merkle). Основная идея заключается в том, чтобы использовать ключи парами, состоящими из ключа зашифрования и ключа расшифрования, которые невозможно вычислить один из другого.
В 1976 г. вышла основополагающая работа [1]. С этого времени было создано много алгоритмов, использующих концепцию открытых ключей. Алгоритм является общедоступным, нет необходимости в секретных каналах связи. Общая схема выглядит следующим образом:
- Каждый пользователь генерирует пару ключей: один для шифрования, другой для расшифрования.
- Каждый пользователь публикует свой ключ шифрования, размещает его в открытом для всех доступе. Второй ключ, соответствующий открытому, сохраняется в секрете.
- Если пользователь A собирается послать сообщение пользователю B, он шифрует сообщение открытым ключом пользователя B.
- Когда пользователь B получает сообщение, он расшифровывет его с помощью своего личного (секретного) ключа. Другой получатель не сможет расшифровать сообщение, поскольку личный ключ B знает только B.
Мы подробно представим алгоритм RSA, являющийся популярным в приложениях.
8.1 Описание алгоритма RSA
В 1978 г. появилась работа [2], в которой Рон Райвест (Ron Rivest), Ади Шамир (Adi Shamir) и Лен Адлеман (Len Adleman) предложили алгоритм с открытым ключом. Схема Райвеста-Шамира-Адлемана (RSA) получила широкое распространение.
Опишем процесс шифрования. Исходный текст должен быть переведен в числовую форму, этот метод считается известным. В результате этого текст представляется в виде одного большого числа. Затем полученное число разбивается на части (блоки) так, чтобы каждая из них была числом в промежутке ![[0, N - 1]](/sites/default/files/tex_cache/832f3983d21c0cdcc22f6aa7c443b641.png) (о выборе
(о выборе  - см. ниже). Процесс шифрования одинаков для каждого блока. Поэтому мы можем считать, что блок исходного текста представлен числом
- см. ниже). Процесс шифрования одинаков для каждого блока. Поэтому мы можем считать, что блок исходного текста представлен числом  ,
,  .
.
Каждый абонент вырабатывает свою пару ключей. Для этого он генерирует два больших простых числа  и
и  , вычисляет произведение
, вычисляет произведение 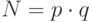 . Затем он вырабатывает случайное число
. Затем он вырабатывает случайное число  , взаимно простое со значением
, взаимно простое со значением 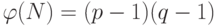 функции Эйлера от числа
функции Эйлера от числа  , и находит число
, и находит число 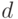 из условия
из условия  . Так как
. Так как 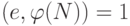 , то такое число
, то такое число 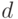 существует и оно единственно. Пару
существует и оно единственно. Пару 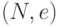 он объявляет открытым ключом и помещает в открытый доступ. Пара
он объявляет открытым ключом и помещает в открытый доступ. Пара  является секретным ключом. Для расшифрования достаточно знать секретный ключ. Числа
является секретным ключом. Для расшифрования достаточно знать секретный ключ. Числа  ,
,  ,
,  в дальнейшем не нужны, поэтому их можно уничтожить.
в дальнейшем не нужны, поэтому их можно уничтожить.
Пользователь  , отправляющий сообщение
, отправляющий сообщение  абоненту
абоненту  , выбирает из открытого каталога пару
, выбирает из открытого каталога пару 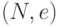 абонента
абонента  и вычисляет шифрованное сообщение
и вычисляет шифрованное сообщение 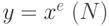 . Чтобы получить исходный текст, абонент
. Чтобы получить исходный текст, абонент  вычисляет
вычисляет  . Так как
. Так как 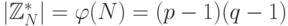 , и
, и 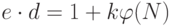 для некоторого целого числа
для некоторого целого числа  , то
, то
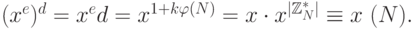
Пример 8.1. Построим криптосистему RSA с 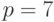 ,
,  и зашифруем сообщение
и зашифруем сообщение 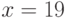 .
.
Находим:  ,
, 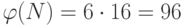 . Выбираем значение
. Выбираем значение  с условиями
с условиями 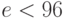 и
и 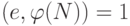 . Например, возьмём
. Например, возьмём 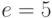 . Находим
. Находим  . Получаем
. Получаем 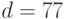 , так как
, так как 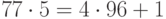 . Открытый ключ:
. Открытый ключ: 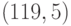 , секретный ключ:
, секретный ключ:  . Для зашифрования число
. Для зашифрования число 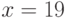 возводим в степень
возводим в степень 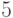 по модулю
по модулю  :
:

Итак, 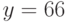 . Расшифрование даёт:
. Расшифрование даёт:

Для ускорения возведения в степень по модулю необходимо использовать быстрый алгоритм возведения в степень, рассмотренный в первой лекции.
8.1.1. О стойкости RSA
Безопасность алгоритма RSA основана на трудоемкости разложения на множители больших чисел. Международная группа ученых вычислителей в январе 2010 года установила новый рекорд факторизации, разложив на простые множители 232-значное число. Следовательно, выбираемое N должно быть больше. Большинство общепринятых алгоритмов вычисления простых чисел  и
и  носят вероятностный характер.
носят вероятностный характер.
8.1.2. О выборе чисел p и q
Для работы алгоритма RSA нужны большие простые числа. Существуют два подхода.
- Генерация случайных чисел и последующя проверка их на простоту с помощью вероятностных тестов. Недостаток такого подхода в том, что числа будут простыми только с какой-то (очень высокой) вероятностью.
- Генерация доказуемо простых чисел. Для этого существуют рекуррентные алгоритмы
Кроме разрядности  и
и  , к ним предъявляются следующие дополнительные требования:
, к ним предъявляются следующие дополнительные требования:
- числа не должны содержаться в списках известных больших простых чисел;
- они не должны быть близкими, так как иначе можно воспользоваться для факторизации
 методом Ферма и решить уравнение
методом Ферма и решить уравнение

- В алгоритме RSA всегда есть эквивалентные по расшифрованию показатели степеней, например
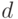 и
и 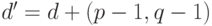 . При этом эквивалентных решений тем больше, чем больше
. При этом эквивалентных решений тем больше, чем больше 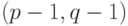 . В лучшем случае
. В лучшем случае 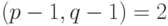 ,
,  ,
,  , где
, где 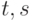 - нечетые взаимно простые числа.
- нечетые взаимно простые числа.
Чтобы исключить возможность применения методов факторизации, накладывают следующее ограничение: числа  ,
, 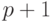 ,
,  ,
,  не должны разлагаться в произведение маленьких простых множителей, должны содержать в качестве сомножителя хотя бы одно большое простое число. В 1978 г. Райвест сформулировал наиболее сильные требования:
не должны разлагаться в произведение маленьких простых множителей, должны содержать в качестве сомножителя хотя бы одно большое простое число. В 1978 г. Райвест сформулировал наиболее сильные требования:
Числа 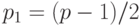 ,
, 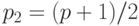 ,
, 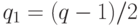 ,
, 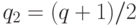 должны быть простыми, причем
должны быть простыми, причем 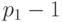 и
и 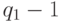 не должны разлагаться в произведение маленьких простых чисел.
не должны разлагаться в произведение маленьких простых чисел.
8.1.3. О выборе параметров e и d
Рассмотрим вопрос о выборе экспонент шифрования и расшифрования. Так как значения  и
и 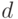 определяют время зашифрования и расшифрования, то можно назвать ряд ситуаций, в которых желательно иметь малое значение
определяют время зашифрования и расшифрования, то можно назвать ряд ситуаций, в которых желательно иметь малое значение  и
и 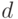 . Например, при использовании системы RSA при защите электронных платежей с применением кредитных карточек естественным является требование использования небольших значений экспоненты
. Например, при использовании системы RSA при защите электронных платежей с применением кредитных карточек естественным является требование использования небольших значений экспоненты 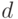 у владельца карточки и большого значения экспоненты
у владельца карточки и большого значения экспоненты  у центрального компьютера.
у центрального компьютера.
Однако выбор малых параметров  или
или 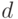 представляется небезопасным по ряду соображений. Если малым является секретный параметр
представляется небезопасным по ряду соображений. Если малым является секретный параметр 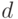 , то можно применить метод перебора малых значений до получения искомого числа
, то можно применить метод перебора малых значений до получения искомого числа 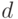 . А если малым является параметр
. А если малым является параметр  , то достаточно большое число открытых сообщений, удовлетворяющих неравенству
, то достаточно большое число открытых сообщений, удовлетворяющих неравенству ![x < \sqrt[e]{N}](/sites/default/files/tex_cache/5af7ed87ef234daaf0d68a5466f9827d.png) , будут зашифровываться простым возведением в степень
, будут зашифровываться простым возведением в степень  , и поэтому их можно найти путем извлечения корня степени
, и поэтому их можно найти путем извлечения корня степени  .
.
Другая аналогичная ситуация может сложиться, когда у нескольких абонентов используется одинаковая экспонента  . Тогда становится возможна атака на основе китайской теоремы об остатках (см. ниже).
. Тогда становится возможна атака на основе китайской теоремы об остатках (см. ниже).
8.1.4. Подготовка текста к шифрованию
Сначала нужно каким-либо способом представить текст сообщения в виде упорядоченного набора чисел по модулю  . Это еще не процесс шифрования, а только подготовка к нему.
. Это еще не процесс шифрования, а только подготовка к нему.
Пример 8.2.Подготовим к зашифрованию девиз ПОЗНАЙ СЕБЯ,
Для простоты предположим, что текст сообщения содержит \ слова, записанные только заглавными буквами. Первый шаг состоит в замене каждой буквы сообщения числом. Будем использовать таблицу замен 8.1.
| А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| С | Т | У | Ф | X | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я | \_ | |
| 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 99 |
Текст ПОЗНАЙ СЕБЯ после замен букв на числа принимает вид: 2524172310199927151141.
Пусть в нашем примере  ,
, 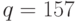 , тогда
, тогда 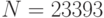 . Поэтому цифровое представление открытого текста нужно разбить на блоки, меньшие, чем
. Поэтому цифровое представление открытого текста нужно разбить на блоки, меньшие, чем  . Одно из таких разбиений выглядит следующим образом:
. Одно из таких разбиений выглядит следующим образом:
2524 1723 10199 9271 511 41
Конечно, выбор блоков неоднозначен, но и не совсем произволен. Например, во избежание двусмысленностей, на стадии расшифровки не следует выделять блоки, начинающиеся с нуля.
При расшифровке сообщения получаем последовательность блоков, затем их соединяем вместе и получаем число. После этого числа заменяют буквами в соответствии с таблицей, приведенной выше.
Обратим внимание на то, что в этом примере каждую букву кодируем двузначным числом. Это сделано для предотвращения неоднозначности. Если бы мы пронумеровали буквы не по порядку, начиная с 1, т. е. А соответствует 1, Б соответствует 2 и т. д., то было бы непонятно, что обозначает блок 12: пару букв АБ или букву Л, двенадцатую букву алфавита. Конечно, для кодирования можно использовать любые однозначные соответствия между буквами и числами, например ASCII-кодировку, что чаще всего и делается.
Продолжим пример: выбираем  ,
, 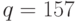 , вычисляем
, вычисляем  . Теперь нужно выбрать число
. Теперь нужно выбрать число  , взаимно простое с
, взаимно простое с  . Наименьшее простое число, не делящее
. Наименьшее простое число, не делящее  , равно
, равно 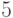 . Положим
. Положим 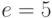 . Зашифруем сообщение поблочно. Для шифрования первого блока вычисляем
. Зашифруем сообщение поблочно. Для шифрования первого блока вычисляем  . Далее,
. Далее,


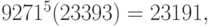


Теперь шифрованный текст имеет вид:  .
.
В нашем примере 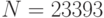 ,
,  . Расширенный алгоритм Евклида для чисел
. Расширенный алгоритм Евклида для чисел  и
и 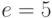 даёт:
даёт:
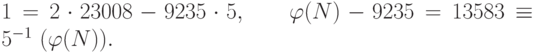
Значит для расшифровки блоков шифртекста мы должны возвести блоки в степень  по модулю
по модулю  . Для первого блока
. Для первого блока 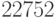 шифртекста в примере получим:
шифртекста в примере получим:

Разбиение числа на блоки можно произвести различными способами. При этом промежуточные результаты зависят от способа разбиения, однако конечный результат - не зависит.

