Смысл энтропии Шеннона
Энтропия д.с.в. - это минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной д.с.в.
Рассмотрим пример (скачки). В заезде участвуют 4 лошади с равными шансами на
победу, т.е. вероятность победы каждой лошади равна 1/4. Введем д.с.в.  , равную номеру победившей лошади. Здесь
, равную номеру победившей лошади. Здесь 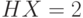 .
После каждого заезда по каналам связи достаточно будет передавать два
бита информации о номере победившей лошади. Кодируем номер лошади следующим
образом: 1-00, 2-01, 3-10, 4-11. Если ввести функцию
.
После каждого заезда по каналам связи достаточно будет передавать два
бита информации о номере победившей лошади. Кодируем номер лошади следующим
образом: 1-00, 2-01, 3-10, 4-11. Если ввести функцию 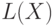 ,
которая возвращает длину сообщения, кодирующего заданное значение
,
которая возвращает длину сообщения, кодирующего заданное значение  , то м. о.
, то м. о.  - это средняя длина сообщения, кодирующего
- это средняя длина сообщения, кодирующего  . Можно формально определить
. Можно формально определить  через две функции
через две функции  , где
, где  каждому значению
каждому значению  ставит в соответствие
некоторый битовый код, причем, взаимно однозначно, а
ставит в соответствие
некоторый битовый код, причем, взаимно однозначно, а  возвращает длину в битах для
любого конкретного кода. В этом примере
возвращает длину в битах для
любого конкретного кода. В этом примере 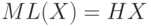 .
.
Пусть теперь д.с.в.  имеет
следующее распределение
имеет
следующее распределение


 бит/сим или м. о.
бит/сим или м. о. 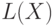 .
Действительно,
.
Действительно, 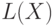 сейчас задается следующим
распределением вероятностей:
сейчас задается следующим
распределением вероятностей:  ,
,  ,
,  . Следовательно,
. Следовательно,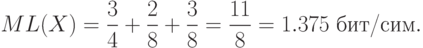
 .
.Можно доказать, что более эффективного кодирования для двух рассмотренных случаев не существует.
То, что энтропия Шеннона соответствует интуитивному представлению о мере
информации, может быть продемонстрировано в опыте по определению среднего
времени психических реакций. Опыт заключается в
том, что перед испытуемым человеком зажигается одна из  лампочек, которую он должен указать. Проводится большая серия испытаний, в которых
каждая лампочка зажигается с определенной вероятностью
лампочек, которую он должен указать. Проводится большая серия испытаний, в которых
каждая лампочка зажигается с определенной вероятностью 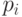
 ,
где
,
где  - это номер лампочки. Оказывается, среднее
время, необходимое для правильного ответа испытуемого, пропорционально
величине энтропии
- это номер лампочки. Оказывается, среднее
время, необходимое для правильного ответа испытуемого, пропорционально
величине энтропии  , а не числу лампочек
, а не числу лампочек  , как можно было бы подумать. В этом опыте предполагается, что чем больше
информации будет получено человеком, тем дольше будет время ее обработки
и, соответственно, реакции на нее.
, как можно было бы подумать. В этом опыте предполагается, что чем больше
информации будет получено человеком, тем дольше будет время ее обработки
и, соответственно, реакции на нее.
Упражнение 13
Найти энтропию д.с.в.  и среднюю длину каждого из приведенных
кодов для этой д.с.в.
и среднюю длину каждого из приведенных
кодов для этой д.с.в.

Упражнение 14
д.с.в.  равна количеству "гербов", выпавших на двух
идеальных монетках. Найти энтропию
равна количеству "гербов", выпавших на двух
идеальных монетках. Найти энтропию  . Придумать минимальный код
для
. Придумать минимальный код
для  , вычислить его среднюю длину и обосновать его минимальность.
, вычислить его среднюю длину и обосновать его минимальность.
Упражнение 15
д.с.в.  задана распределением
задана распределением  ,
,  Найти
энтропию этой д.с.в. Придумать минимальный код для
Найти
энтропию этой д.с.в. Придумать минимальный код для  , вычислить
его среднюю длину и обосновать его минимальность.
, вычислить
его среднюю длину и обосновать его минимальность.
Упражнение 16
Про д.с.в.  известно, что ее значениями являются буквы
кириллицы. Произведен ряд последовательных измерений
известно, что ее значениями являются буквы
кириллицы. Произведен ряд последовательных измерений  , результат
которых - "ТЕОРИЯИНФОРМАЦИИ". Составить на основании этого результата
приблизительный закон распределения вероятностей этой д.с.в. и оценить
минимальную среднюю длину кодов для
, результат
которых - "ТЕОРИЯИНФОРМАЦИИ". Составить на основании этого результата
приблизительный закон распределения вероятностей этой д.с.в. и оценить
минимальную среднюю длину кодов для  .
.
Семантическая информация
В 50-х годах XX века появились первые попытки определения
абсолютного информационного содержания предложений естественного языка.
Стоит отметить, что сам Шеннон однажды заметил, что смысл сообщений
не имеет никакого отношения к его теории информации, целиком построенной
на положениях теории вероятностей. Но его способ точного измерения
информации наводил на мысль о возможности существования способов
точного измерения информации более общего вида, например, информации из
предложений естественного языка. Примером одной из таких мер является функция  , где
, где  - это предложение,
смысловое содержание
которого измеряется,
- это предложение,
смысловое содержание
которого измеряется,  - вероятность истинности
- вероятность истинности  . Вот некоторые свойства этой функции-меры:
. Вот некоторые свойства этой функции-меры:
- если
 (из
(из  следует
следует 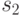 ) - истинно, то
) - истинно, то  ;
; -
 ;
; - если
 - истинно, то
- истинно, то 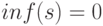 ;
; -
 , т.е. независимости
, т.е. независимости  и
и 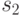 .
.
Значение этой функции-меры больше для предложений,
исключающих большее количество возможностей. Пример: из  -
"
-
" 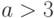 " и
" и 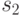 - "
- " 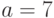 " следует, что
" следует, что  или
или 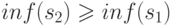 ; ясно, что
; ясно, что 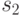 исключает больше
возможностей, чем
исключает больше
возможностей, чем  .
.
Для измерения семантической информации также используется
функция-мера  . Ясно, что
. Ясно, что 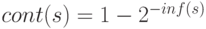 или
или  .
.
Упражнение 17
Вычислить 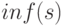 и
и  предложения
предложения  , про которое известно,
что оно достоверно на 50%, и предложения
, про которое известно,
что оно достоверно на 50%, и предложения 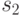 , достоверность
которого 25%.
, достоверность
которого 25%.

