|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Криптосистемы
15.2. Криптографическая система Эль-Гамаля
Помимо RSA и криптографической системы Рабина есть другая криптосистема с открытым ключом Эль-Гамаля (ElGamal), которая названа по имени ее изобретателя, Тахира Эль-Гамаля (Taher ElGamal). Криптосистема Эль-Гамаля базируется на свойствах дискретного логарифма, который обсуждался в лекциях 12-13.
Криптографическая система Эль-Гамаля
На основании сведений лекций 12-13, если p — очень большое простое число, e1 — первообразный корень в группе 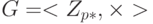 и r — целое число, тогда e2 = e1r mod p просто вычисляется с использованием быстрого показательного алгоритма (метод "возведения в квадрат и умножения"). Но по данным e2, e1 и p, невозможно вычислить r = loge1e2 mod p (проблема дискретного логарифма).
и r — целое число, тогда e2 = e1r mod p просто вычисляется с использованием быстрого показательного алгоритма (метод "возведения в квадрат и умножения"). Но по данным e2, e1 и p, невозможно вычислить r = loge1e2 mod p (проблема дискретного логарифма).
Процедура
Рисунок 15.2 показывает генерацию ключей, шифрование и дешифрование в криптосистеме Эль-Гамаля.
Генерация ключей
Боб использует шаги, показанные в алгоритме 15.4, чтобы создать свои общедоступный и частный ключи.
ElGamal_Key_Generation
{
Выберите большое простое число p
Выберите d, члена группы G = < Zp*, x > , такое, что 1 < d < p – 2
Выберите e1 — первообразный корень в группе G = < Zp*, x >
e2 <- e1d mod p
Общедоступный_ключ <- (e1, e2, p) // Может быть объявлен публично
Частный_ключ <- -d // Должен сохраняться в секрете
return Общедоступный_ключ и Частный_ключ
}
15.4.
Генерация ключей в криптосистеме Эль-Гамаля
Шифрование
Любой может передать сообщение Бобу, используя его открытый ключ доступа. Процесс шифрования показан в алгоритме 15.5. Если применяется быстрый показательный алгоритм (см. лекции 12-13), шифрование в криптосистеме Эль-Гамаля может также быть выполнено по времени с полиномиальной сложностью.
ElGamal_Encryption (e1, e2, p) // P — исходный текст
{
Выберите случайное целое число r в группе G = < Zp*, x >
C1 <- e1r mod p
C2 <- (P x e2r) mod p // C1 и C2 – зашифрованные тексты
return C1 и C2 }
15.5.
Шифрование в криптосистеме Эль-Гамаля
Дешифрование
Боб может использовать алгоритм 15.6, чтобы расшифровать полученное сообщение зашифрованного текста.
ElGamal_Decryption {d, p, C1, C2) // C1 и C2 — зашифрованный текст
{
P <- [C2(C1d)-1] mod p // P — исходный текст
return P
}
15.6.
Алгоритм 15.6. Дешифрование в криптосистеме Эль-Гамаля
Доказательство
Криптосистема Эль-Гамаля проводит дешифрацию согласно выражению 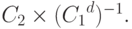 Это выражение может быть проверено с помощью подстановки P:
Это выражение может быть проверено с помощью подстановки P:
![[{C_2} \times {\left( {{C_1}^d} \right]^{ - 1}}\bmod p = [({e_2}^r \times P) \times {\left( {{e_1}^{rd}} \right]^{-1}}\bmod p = \left( {{e_1}^{rd}} \right) \times P \times {\left( {{e_1}^{rd}} \right)^{ - 1}} = P](/sites/default/files/tex_cache/ce307f2c84b0017a0aac708068e7ec22.png)
Пример 15.2
Рассмотрим тривиальный пример. Боб выбирает 11 в качестве p. Затем он выбирает e1 = 2. Обратите внимание, что 2 — первообразный корень в Z11* (см. приложение J). Затем Боб выбирает d = 3 и вычисляет e2 = e1d = 8. Получены открытые ключи доступа — (2, 8, 11) и секретный ключ — 3. Алиса выбирает r = 4 и вычисляет C1 и C2 для исходного текста 7.
Исходный текст: 7 C1 = e1r mod 11 = 16 mod 11= 5 mod 11 C2 = (P x e2r) mod 11 = (7 x 4096) mod 11 = 6 mod 111 Зашифрованный текст: (5, 6)
Боб получает зашифрованные тексты ( 5 и 6 ) и вычисляет исходный текст.
Зашифрованный текст: [C1 x (C2d)-1] mod 11 = 6 x (53)-1 mod 11 = 6 x 3 mod 11 = 7 mod 11 Исходный текст: 7
Пример 15.3
Вместо того чтобы использовать ![P = [{C_2}{({C_1}^d)^{-1}}]\bmod p](/sites/default/files/tex_cache/9aed43fd4361259c057dd6fa3eeeb435.png) для дешифрования, мы можем избежать вычисления мультипликативной инверсии и применить
для дешифрования, мы можем избежать вычисления мультипликативной инверсии и применить ![P = [{C_2}{({C_1}^{p - 1 - d})^{-1}}]\bmod p](/sites/default/files/tex_cache/2959d03d4d91979220e8c17274aa1d27.png) (см. малую теорему Ферма в лекциях 12-13). В Примере 15.2 мы можем вычислить
(см. малую теорему Ферма в лекциях 12-13). В Примере 15.2 мы можем вычислить ![P = [6 \times {5^{11 - 1 - 3}}]\bmod {\text{ }}11 = 7{\text{ }}\bmod {\text{ }}11](/sites/default/files/tex_cache/68e0680d24d24dfd6054bcd928d73d15.png) .
.
Анализ
Очень интересная черта криптосистемы Эль-Гамаля — то, что Алиса создает r и сохраняет его в секрете; Боб создает d и сохраняет его в секрете. Это затруднение криптографической системы может быть решено следующим образом:
a. Алиса передает ![{C_2} = [{e_2}^r \times P]{\text{ }}\bmod {\text{ }}p = [({e_1}^{rd}) \times P]{\text{ }}\bmod {\text{ }}p](/sites/default/files/tex_cache/cad271330e012a6d111810cd5e02e58b.png) . Выражение ( e1rd ) действует как маска, которая скрывает значение P. Чтобы найти значение P, Боб должен удалить эту маску.
. Выражение ( e1rd ) действует как маска, которая скрывает значение P. Чтобы найти значение P, Боб должен удалить эту маску.
b. Поскольку используется модульная арифметика, Боб должен создать точную копию маски и инвертировать ее (мультипликативная инверсия), чтобы снять воздействие маски.
c. Алиса передает Бобу C1 = e1r, что является частью маски. Боб должен вычислить C1d, чтобы cделать точную копию маски, поскольку C1d = (e1r') d= (e1 rd). Другими словами, после получения точной копии маски Боб инвертирует ее и умножает результат на C2, чтобы удалить маску.
d. Это можно представить так, что Боб помогает Алисе сделать маску (e1rd), не показывая значение d ( d уже включено в e2 = e1rd ); Алиса помогает Бобу делать маску ( e1 rd ), не раскрывая значение r ( r уже включено в C1 = e1r ).


