Алгоритмы симметричного шифрования. Часть 2

Дешифрование

Процесс дешифрования аналогичен процессу шифрования. Дешифрование состоит в использовании зашифрованного текста в качестве входа в ту же самую структуру IDEA, но с другим набором ключей. Дешифрующие ключи U₁, . . . , U₅₂ получаются из шифрующих ключей следующим образом:

1. Первые четыре подключа i-ого раунда дешифрования получаются из первых четырех подключей (10-i)-го раунда шифрования, где стадия заключительного преобразования считается 9-м раундом. Первый и четвертый ключи дешифрования эквивалентны мультипликативной инверсии по модулю ( 2¹⁶ + 1 ) соответствующих первого и четвертого подключей шифрования. Для раундов со 2 по 8 второй и третий подключи дешифрования эквивалентны аддитивной инверсии по модулю ( 2¹⁶ ) соответствующих третьего и второго подключей шифрования. Для раундов 1 и 9 второй и третий подключи дешифрования эквивалентны аддитивной инверсии по модулю ( 2¹⁶ ) соответствующих второго и третьего подключей шифрования.
2. Для первых восьми раундов последние два подключа i раунда дешифрования эквивалентны последним двум подключам ( 9 - i ) раунда шифрования.

Для мультипликативной инверсии используется нотация Z_j^-1, т.е.:

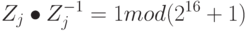
Так как 2¹⁶ + 1 является простым числом, каждое ненулевое целое Z_j <= 2¹⁶ имеет уникальную мультипликативную инверсию по модулю ( 2¹⁶ + 1 ). Для аддитивной инверсии используется нотация ( -Z_j ), таким образом, мы имеем: -Z_j + Z_j = 0 mod (2¹⁶)

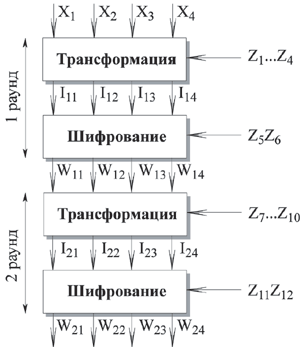
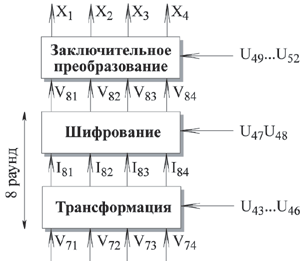
Для доказательства того, что алгоритм дешифрования с соответствующими подключами имеет корректный результат, рассмотрим одновременно процессы шифрования и дешифрования. Каждый из восьми раундов разбит на две стадии преобразования, первая из которых называется трансформацией, а вторая шифрованием.

Рис. 3.5. Шифрование IDEA

Рис. 3.6. Дешифрование IDEA

Рассмотрим преобразования, выполняемые в прямоугольниках на обоих рисунках. При шифровании поддерживаются следующие соотношения на выходе трансформации:

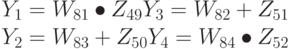
Первая стадия первого раунда процесса дешифрования поддерживает следующие соотношения:

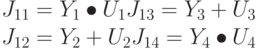
Подставляя соответствующие значения, получаем:

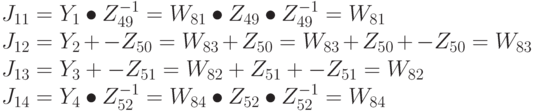
Таким образом, выход первой стадии процесса дешифрования эквивалентен входу последней стадии процесса шифрования за исключением чередования второго и третьего блоков. Теперь рассмотрим следующие отношения:

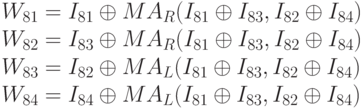
Где MA_R(X, Y) есть правый выход МА структуры с входами Х и Y, и MA_L(X, Y) есть левый выход МА структуры с входами Х и Y. Теперь получаем

Аналогично мы имеем

V12 = I83
V13 = I82
V14 = I84

Таким образом, выход второй стадии процесса дешифрования эквивалентен входу предпоследней стадии процесса шифрования за исключением чередования второго и третьего подблоков. Аналогично можно показать, что

V81 = I11
V82 = I13
V83 = I12
V84 = I14

Наконец, так как выход трансформации процесса дешифрования эквивалентен первой стадии процесса шифрования за исключением чередования второго и третьего подблоков, получается, что выход всего процесса шифрования эквивалентен входу процесса шифрования.