| Россия, Новосибирск, НГПУ, 2009 |
Разработка сложных параллельных программ с использованием MPI
Цель - изучить параллельный алгоритм Фокса перемножения матриц и реализовать его с применением MPI; получить экспериментальные данные о масштабируемости данного алгоритма.
В данном занятии изучаются 2 параллельных алгоритма перемножения матриц:
- с декомпозицией по строкам,
- с блочной декомпозицией.
Ниже в тексте предполагается, что матрицы являются квадратными порядка N (т.е., они являются N х N матрицами). Тип элементов матриц может быть выбран произвольным - целочисленный, с плавающей точкой, с плавающей точкой двойной точности, и т.п.
Задача 1. Требуется реализовать параллельный алгоритм перемножения матриц с использованием декомпозиции по строкам. Пусть даны исходные матрицы A, B, а C является результирующей матрицей, т.е., C = A x B.
Предполагается, что для матриц порядка N алгоритм выполняется на N процессорах. Соответственно, i -ая строка матриц A,B назначается процессору i, и процессор i ответственен за вычисление i -ой строки результирующей матрицы C.
Суть алгоритма заключается в нахождении элемента с координатами (i, j) результирующей матрицы С процессом с номером i путем вычисления "поточечного" (скалярного) произведения строки i матрицы А и столбца j матрицы B. Для вычисления этого произведения, процессу i понадобится весь столбец j матрицы B, что может быть реализовано путем применения операции MPI_Allgather во всех процессах:
Альтернативное применению MPI_Allgather может быть решение с предварительной рассылкой всей матрицы B всем процессам.
Оттранслировать и выполнить полученную программу для матриц размером 10x10 с использованием 10 процессоров ( -np 10 ).
Дополнительную информацию об этом алгоритме можно получить со страницы http://www.abo.fi/~Mats.Aspnas/PP2006/handouts/Chapter4.pdf
Задача 2. Требуется реализовать параллельный алгоритм перемножения матриц с блочной декомпозицией (алгоритм Фокса).
В данном алгоритме предполагается, что матрицы размерности N x N распределяются между P процессами, которые организованы в виде декартовой решетки (квадрата) со стороной vP.
Предполагается, что N делится без остатка на vP, а потому каждый процесс хранит подматрицы размерности N' x N', где
N' = N / vP.
Например, при N = 16, т.е., матрицах размерности 16 x 16, и P = 4, т.е., для решетки процессоров 2 х 2, каждый процесс хранит подматрицы размером 8 х 8 исходных матриц A, B, и ответственен за вычисление соответствующей подматрицы результирующей матрицы С.
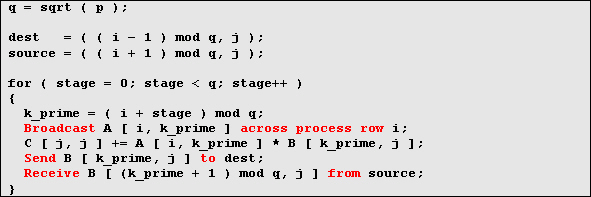
Пусть Aij является подматрицей размерности N' x N' матрицы A, первым элементом которой является элемент A [ i * N', j * N' ] (аналогично для подматриц Bij и Cij ). Подматрицы Aij, Bij и Cij назначаются процессу с номером (i, j). Тогда алгоритм работы процесса с номером (i, j) состоит в следующем:
Реализация данного алгоритма в виде MPI-программы показана ниже:
Оттранслировать и выполнить данную программу для матриц размерности 100х100 с использованием 16 процессоров ( -np 16 ).