Математика и физика Flash

Поворот координат

До этого момента мы постоянно поворачивали точки, линии и векторы. В основном, мы начинали с радиуса от фиксированной точки и затем поворачивали его на определенный угол. Это способ довольно эффективен, однако вспомните, что когда мы рисовали наш корабль или стрелку, нужно было, чтобы они "смотрели" вправо (0 градусов), так как все повороты основывались на вращении чего-либо, начиная с нулевого угла.

Что будет, если поворачивать объект вокруг центральной точки на определенное количество градусов, а этот объект находится под углом, отличным от нулевого? Как быть в случае, если нам известны лишь координаты x и y объекта, а мы хотим вращать его вокруг центральной точки? Давайте рассмотрим следующий случай.

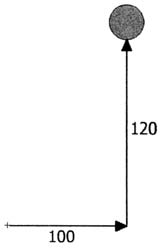
Здесь мы наблюдаем объект, расположенный на координате x=100 и на 120 пикселей выше центральной точки. Теперь предположим, что нам нужно повернуть объект на 20 градусов вокруг центральной точки. Возникает проблема, заключающаяся в том, что объект не находится под углом ноль градусов, с которого можно начать вращение. Можно было бы использовать теорему Пифагора для вычисления расстояния от центра, значение atan2 для выяснения текущего угла объекта, и затем прибавить 20 градусов к этому значению и с помощью sin и cos выяснить новые значения X и Y.

Однако это слишком длинный способ, и можно сделать это гораздо быстрее, особенно в случае с множеством объектов. Сейчас я отклонюсь от привычного способа изложения и приведу формулы без объяснения того, как они были получены. Здесь просто утверждается, что данные формулы работают, поэтому просто запомните их для дальнейшего использования.

Когда нужно повернуть точку (x, y) на определенный угол (angle), нужно использовать следующие выражения.

new_x = x*cos (angle) - y*sin (angle)
  new_y = y*cos (angle) + x*sin (angle)

Я записал это на клочке бумаги и прикрепил на стенку рядом с моим компьютером. Теперь я уже запомнил эти выражения довольно четко.

Заметка: процесс вывода этих формул не является секретной информацией. Это стандартная операция, используемая при повороте координат. Если вам интересно их получение, вы можете найти его в любой книге по тригонометрии и изучить их вывод. Я не рассказываю здесь об этом по той причине, что это выходит за рамки рассматриваемой тригонометрии, применимой к Flash.

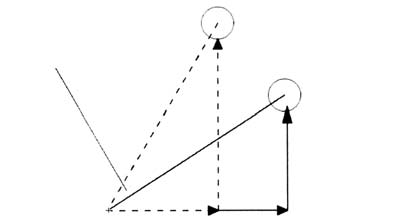
На следующем рисунке изображены связи между x, y и new_x, new_y, а также угол, на который мы поворачиваем объект.

Попробуем применить это на деле во Flash.

Полет кораблей

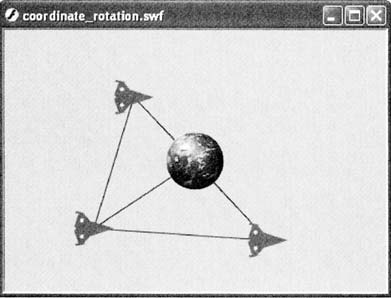
1. Откройте фильм из предыдущего упражнения этой лекции. Вам понадобится лишь фильм в вашей библиотеке Library, который мы сможем использовать в виде объектов для вращения. Добавьте три копии фильма в любые позиции на рабочем столе и назовите их инстансы именами mc1_mc, mc2_mc и mc3_mc. Мы будем вращать их вокруг центра рабочего места, поэтому нарисуйте рисунок в точке (275, 200), который будет играть роль центральной точки. Я изобразил в центре планету Земля, по орбите которой и будут "летать" корабли:
   

   
   
2. Теперь добавьте новый слой с именем actions и введите следующий код в кадре 1.

   init();
     function init() {
       cx = 275;
       cy = 200;
       onEnterFrame = rotate;
       var angle = 2;
       rad = angle*Math.PI/180;
       cosAngle = Math.cos(rad);
       sinAngle = Math.sin(rad);
     }

   Рассмотрим этот код. Функция init будет указывать центральную точку и настраивать функцию onEnterFrame. После этого будет устанавливаться angle для поворота объектов в каждом кадре, с последующим переводом в радианы. Следующие две строки не добавляют ничего в функциональность программы. Однако они обеспечивают должную эффективность. Так как нам понадобится использовать cos и sin угла дважды в каждом кадре фильма, и так как они никогда не изменяются, не имеет смысл вычислять их 30 или 40 раз в секунду! Это будет делаться лишь один раз в начале фильма, с сохранением значений в переменных cosAngle и sinAngle, после чего эти переменные будут использоваться повсеместно в оставшейся части фильма.
3. Теперь мы создадим функцию rotate. Она будет циклически обрабатывать три фильма и применять формулу поворота координат к их позициям.

   function rotate() {
       for (i=1; i<4; i++) {
         x = this["mc"+i+"_mc"]._x-cx;
         у = this["mc"+i+"_mc"]._y-cy;
         x1 = x*cosAngle-y*sinAngle;
         y1 = y*cosAngle+x*sinAngle;
         this["mc"+i+"_mc"]._x = x1+cx;
         this["mc"+i+"_mc"]._y = y1+cy;
       }
     }

   Помните, что всегда необходимо определять, вокруг чего осуществлять вращение - т.е. центральную точку - и в вычислениях отталкиваться именно от этой точки. mc1_mc расположен в точке (375,y), на расстоянии 100 пикселей от центральной точки, и 375 - то значение X, которое мы используем в вычислениях. Следовательно, мы будем вычитать значения центральной точки cx и cy из текущих координат каждого фильма. После этого будет выполняться поворот с присвоением результатов x1 и y1. Это даст новую позицию фильма относительно центральной точки, поэтому нужно прибавить cx и cy для определения наших конечных координат.
4. В качестве последнего небольшого дополнения, добавим несколько функций, рисующих линии, для визуализации вращения. Приведем окончательный код программы.

   init();
     function init() {
       cx = 275;
       cy = 200;
       onEnterFrame = rotate;
       var angle = 2;
       rad = angle*Math.PI/180;
       cosAngle = Math.cos(rad);
       sinAngle = Math.sin(rad);
     }
     function rotate() {
       for (i=1; i<4; i++) {
         x = this["mc"+i+"_mc"]._x-cx;
         у = this["mc"+i+"_mc"]._y-cy;
         x1 = x*cosAngle-y*sinAngle;
         y1 = y*cosAngle+x*sinAngle;
         this["mc"+i+"_mc"]._x = x1+cx;
         this["mc"+i+"_mc"]._y = y1+cy;
         clear ();
         lineStyle (1, 0, 80);
         moveTo (mc1_mc._x, mc1_mc._y);
         lineTo (mc2_mc._x, mc2_mc._y);
         lineTo (mc3_mc._x, mc3_mc._y);
         lineTo (me1_mc._x, mc1_mc._y);
         moveTo(cx, cy);
         lineTo (mc1_mc._x, mc1_mc._y);
         moveTo (cx, cy);
         lineTo (mc2_mc._x, mc2_mc._y);
         moveTo (cx, cy);
         lineTo (mc3_mc._x, mc3_mc._y);
       }
     }

   Пример 8.4.
5. Запустите фильм. Вы увидите три фильма, поворачивающиеся вокруг центральной точки. Если вы хотите сравнить ваш файл с моим, вы можете использовать coordinate_rotation.fla в исходных файлах.
   

   
   

Проект №2: Bounce

Наш последний проект будет включать в себя практически весь спектр рассмотренного до сих пор материала. Мы не будем рассматривать другие новые концепции, а будем комбинировать уже реализованные идеи для достижения некоторых совершенно новых эффектов. С помощью материала, изученного в последних лекциях, вы можете создавать бесчисленное количество интересных эффектов. Нужно просто искать новые способы применения принципов программирования и их различных комбинаций. Разумеется, все, что вы узнаете с этого момента, будет только преумножать ваши знания по мере того, как вы будете пытаться комбинировать новое с уже изученным материалом. Итак, приступим.

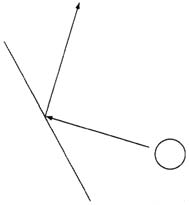
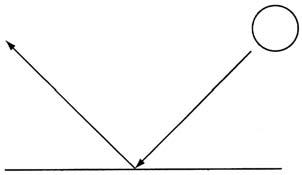
До сих пор мы рассматривали объекты, отскакивающие от прямых "стен", "полов" и "потолков". Но что будет, если стена не прямая? Предположим, что шарик движется под углом 57 градусов и ударяется о стену, наклоненную под углом 32 градуса. Под каким углом и с какой скоростью в этом случае он отскочит? Сейчас у нас есть все средства для выяснения этого. Рассмотрим следующий рисунок.

Шарик движется под определенным углом, ударяется о стенку и отскакивает под показанным углом. Теперь, перед тем, как расстраиваться из-за того, что это может оказаться очень трудным для понимания, обратимся к следующему рисунку.

Это несложный случай, не так ли? Ничуть не сложнее того, что мы реализовали в игре "pong". Здесь просто осуществляется проверка того, находится ли шарик ниже уровня пола, и обращается в отрицательную скорость по направлению Y. Два этих рисунка по сути представляют собой одно и тоже. Я просто повернул второй из них, чтобы сделать пол расположенным горизонтально. Стратегия такова: мы поворачиваем всю конструкцию, чтобы реализовать действие для случая с плоским полом, выполняем действия для отскакивания шарика, затем поворачиваем все обратно. На самом деле нам нужно поворачивать не только координаты X и Y шарика, но также его скорости X и Y (представлены первой стрелкой на рисунке). (Это файл c hapter8-final.fla на компакт-диске).

1. Сначала нарисуем стену. Это будет просто прямая горизонтальная линия в фильме, с именем инстанса wall_mc, и создадим шарик с именем ball_mc.
2. Повернем стену вручную, но не больше, чем на +90 или -90 градусов.
3. Теперь давайте создадим функцию init, которая будет обеспечивать гравитацию, отскакивание шарика, определять функцию onEnterFrame, а также сделаем наш шарик перетаскиваемым и бросаемым.

   init();
     function init() {
       // set some constants
       grav = .5;
       bounce = -.8;
       TOP = 0;
       BOTTOM = Stage.height;
       LEFT = 0;
       RIGHT = Stage.width;
       // our animation function
       onEnterFrame = move;
       // make the ball draggable
       ball_mc.onPress = function() {
         this.startDrag();
         this.dragging = true;
       };
       ball_mc.onRelease = ball_mc.onReleaseOutside=function() {
         this.stopDrag();
         this.dragging = false;
       };
     }
4. После этого мы определим нашу главную функцию move, без проверки коллизий.

   function move() {
       // if we are not dragging the ball
       if (!ball_mc.dragging) {
         // add gravity to the у velocity
         ball_mc.velY += grav;
         // add velocity to the position
         ball_mc._x += ball_mc.velX;
         ball_mc._y += ball_mc.velY;
         // if ball hits any wall, position it at the edge of the wall
         // and have it bounce
         if (ball_mc._x<LEFT+ball_mc._width/2) {
           ball_mc._x = LEFT+ball_mc._width/2;
           ball_mc.velX *= bounce;
         } else if (ball_mc._x>RIGHT-ball_mc._width/2) {
           ball_mc._x = RIGHT-ball_mc._width/2;
           ball_mc.velX *= bounce;
         } else if (ball_mc._y<OP+ball_mc._height/2) {
           ball_mc._y = TOP+ball_mc._height/2;
           ball_mc.velY *= bounce;
         } else if (ball_mc._y>BOTTOM-ball_mc.__height/2) {
           ball_mc._y = BOTTOM-ball_mc._height/2;
           ball_mc.velY *= bounce;
         }
       } else {
         // if we ARE dragging the ball
         // velocity = new position - old position
         ball_mc.velX = ball_mc._x-ball_mc.oldx;
         ball_mc.velY = ball_mc._y-ball_mc.oldy;
         // reset old position for next time
         ball_mc.oldx = ball_mc._x;
         ball_mc.oldy = ball_mc._y;
       }
     }

   Пример 8.5.

   Здесь содержится довольно большое количество кода, однако он уже весь вам знаком.
5. Так как наш код обеспечения проверки столкновений и отскакивания шарика будет довольно сложным, мы переместим его в его собственную функцию. Вставьте эту строку сразу после определения параметров _x и _y фильма ball_mc.

   checkWall (wall_mc);