Методы кластерного анализа. Иерархические методы
Иерархический кластерный анализ в SPSS
Рассмотрим процедуру иерархического кластерного анализа в пакете SPSS (SPSS). Процедура иерархического кластерного анализа в SPSS предусматривает группировку как объектов (строк матрицы данных), так и переменных (столбцов) [54]. Можно считать, что в последнем случае роль объектов играют строки, а роль переменных - столбцы.
В этом методе реализуется иерархический агломеративный алгоритм, смысл которого заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, в ходе алгоритма они объединяются. Вначале выбирается пара ближайших кластеров, которые объединяются в один кластер. В результате количество кластеров становится равным N-1. Процедура повторяется, пока все классы не объединятся. На любом этапе объединение можно прервать, получив нужное число кластеров. Таким образом, результат работы алгоритма агрегирования зависит от способов вычисления расстояния между объектами и определения близости между кластерами.
Для определения расстояния между парой кластеров могут быть сформулированы различные подходы. С учетом этого в SPSS предусмотрены следующие методы:
- Среднее расстояние между кластерами (Between-groups linkage), устанавливается по умолчанию.
- Среднее расстояние между всеми объектами пары кластеров с учетом расстояний внутри кластеров (Within-groups linkage).
- Расстояние между ближайшими соседями - ближайшими объектами кластеров (Nearest neighbor).
- Расстояние между самыми далекими соседями (Furthest neighbor).
- Расстояние между центрами кластеров (Centroid clustering) или центроидный метод. Недостатком этого метода является то, что центр объединенного кластера вычисляется как среднее центров объединяемых кластеров, без учета их объема.
- Метод медиан - тот же центроидный метод, но центр объединенного кластера вычисляется как среднее всех объектов (Median clustering).
- Метод Варда.
Пример иерархического кластерного анализа
Порядок агломерации (протокол объединения кластеров) представленных ранее данных приведен в таблице 13.2. В протоколе указаны такие позиции:
- Stage - стадии объединения (шаг);
- Cluster Combined - объединяемые кластеры (после объединения кластер принимает минимальный номер из номеров объединяемых кластеров);
- Coefficients - коэффициенты.
Так, в колонке Cluster Combined можно увидеть порядок объединения в кластеры: на первом шаге были объединены наблюдения 9 и 10, они образовывают кластер под номером 9, кластер 10 в обзорной таблице больше не появляется. На следующем шаге происходит объединение кластеров 2 и 14, далее 3 и 9, и т.д.
В колонке Coefficients приведено количество кластеров, которое следовало бы считать оптимальным; под значением этого показателя подразумевается расстояние между двумя кластерами, определенное на основании выбранной меры расстояния. В нашем случае это квадрат евклидова расстояния, определенный с использованием стандартизированных значений. Процедура стандартизации используется для исключения вероятности того, что классификацию будут определять переменные, имеющие наибольший разброс значений. В SPSS применяются следующие виды стандартизации:
- Z-шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
- Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
- Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
- Максимум 1. Значения переменных делятся на их максимум.
- Среднее 1. Значения переменных делятся на их среднее.
- Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Определение количества кластеров
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в процессе агломерации/разделения множества объектов.
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание коэффициента, называемого критерием Е. Скачкообразное увеличение значения критерия Е можно определить как характеристику числа кластеров, которые действительно существуют в исследуемом наборе данных. Таким образом, этот способ сводится к определению скачкообразного увеличения некоторого коэффициента, который характеризует переход от сильно связанного к слабо связанному состоянию объектов.
В таблице 13.2 мы видим, что значение поля Coefficients увеличивается скачкообразно, следовательно, объединение в кластеры следует остановить, иначе будет происходить объединение кластеров, находящихся на относительно большом расстоянии друг от друга.
В нашем примере это скачок с 1,217 до 7,516. Оптимальным считается количество кластеров, равное разности количества наблюдений (14) и количества шагов до скачкообразного увеличения коэффициента (12).
Следовательно, после создания двух кластеров объединений больше производить не следует, хотя визуально мы ожидали появления трех кластеров.
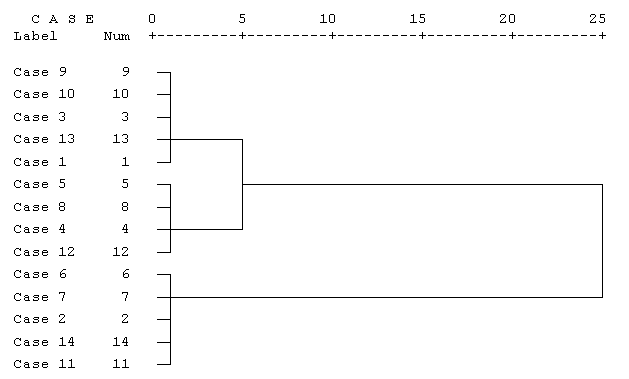
Агрегирование данных может быть представлено графически в виде дендрограммы. Она определяет объединенные кластеры и значения коэффициентов на каждом шаге агломерации (отображены значения коэффициентов, приведенные к шкале от 0 до 25).
Дендрограмма для нашего примера приведена на рис. 13.5. Разрез дерева агрегирования вертикальной чертой дал нам два кластера, состоящих из 9 и 5 объектов.
На верхней линии по горизонтали отмечены номера шагов алгоритма, всего алгоритму потребовалось 25 шагов для объединения всех объектов в один кластер.