|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Методы и средства обеспечения живучести и восстановления работоспособности МКМД-бит-потоковых субпроцессоров
7.6. Оценка качества работы подсистемы локализации и идентификации отказов в МКМД-бит-процессорных матрицах
Как видно из изложенного, при использовании не Tlf -адаптивных алгоритмов тестирования локализация и идентификация отказов проводится по классической схеме аппаратного контроля, которая не зависит от содержимого функциональных микропрограмм. Поэтому объектом диагностики является не субпроцессор, а вся МКМД-бит-процессорная матрица, в которой каждый бит-процессор подтверждает свою работоспособность по всем реализуемым им функциям.
Качество работы подсистемы локализации и идентификации отказов в МКМД-бит-процессорных матрицах определяется тремя основными факторами: конструктивными ограничениями на средства ввода-вывода тестовых микропрограмм и данных, размерами самой бит-матрицы, а также размерами и топологией действующей карты отказов. Все эти факторы взаимозависимы, что делает задачу оценки качества работы подсистемы локализации и идентификации отказов в МКМД-бит-процессорных матрицах нелинейной. При этом основными показателями качества работы подсистемы локализации и идентификации отказов принято считать полноту и время проведения контроля, первый из которых влияет на качество парирования обнаруженных карт отказов, а второй - на темп реального времени работы всего субпроцессора.
В таких условиях работу подсистемы локализации и идентификации отказов проще всего оценить по каждому фактору отдельно, используя в качестве основного ограничения лучшие и худшие значения конструктивных параметров средства ввода-вывода тестовых микропрограмм и данных, то есть конфигурацию интерфейса подсистемы локализации и идентификации отказов, которая может не совпадать с конфигурацией интерфейса субпроцессора.
При оценке качества работы подсистемы локализации и идентификации отказов в МКМД-бит-процессорных матрицах прежде всего необходимо определить условия, при которых еще можно говорить о темпе реального времени. С этой целью определим структуру временных затрат на полное тестирование полностью работающей бит-матрицы, что снимает влияние действующей карты отказов на продолжительность диагностики.
При этом в качестве параметров будем использовать уровень распараллеливания ввода-вывода тестовых микропрограмм и данных:
- Полностью последовательная P -шина, которая обеспечивает максимум временных издержек на ввод тестовых микропрограмм, так как в ней все регистры бит-инструкций объединены в последовательный FIFO -регистровый канал ввода-вывода с однобитным входом и однобитным выходом. При этом FIFO -регистровая D -шина полностью распараллелена по периферийно доступным входам-выходам, что соответствует полнодоступной по периферии бит-матрице рис. 7.18-а.
- Самый худший случай - полностью последовательные FIFO -регистровые P - и D -шины, что соответствует конструкции D -шины рис. 7.18-г и однострочным U -образным Т -рекурсивным тестовым микропрограммам, вводимым в бит-матрицу по однобитной последовательной P -шине.
- Идеальный случай - полностью параллельные FIFO -регистровые P - и D -шины, что соответствует полнодоступной бит-матрице и требует гипрепараллельных гальванических P - и D -шин, реализуемых средствами оптоэлектроники или наноэлектроники.
При таких ограничениях удается ввести алгебраические соотношения для расчета времени тестирования бит-матриц (табл. 7.1-7.3) Tlf -адаптивного контроля бит-матрицы Т -рекурсивными возвратными тестами рисунков, где:
-
 - номер шага тестирования;
- номер шага тестирования; -
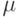 - количество аффинных модификаций исходного многострочного теста (
- количество аффинных модификаций исходного многострочного теста ( 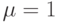 в однострочных тестах);
в однострочных тестах); -
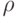 - количество комбинаций тест-данных, образующих одну зондирующую посылку;
- количество комбинаций тест-данных, образующих одну зондирующую посылку; -
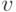 - количество зондирующих посылок, обеспечивающих формирование полной матрицы переходов АЛУ;
- количество зондирующих посылок, обеспечивающих формирование полной матрицы переходов АЛУ; -
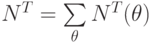 - целочисленное время получения откликов от бит-процессоров одного канала;
- целочисленное время получения откликов от бит-процессоров одного канала; -
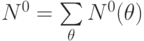 - целочисленное время начальной задержки при получении первого отклика тестируемого канала;
- целочисленное время начальной задержки при получении первого отклика тестируемого канала; -
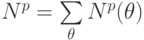 - целочисленное время загрузки тестовой микропрограммы в бит-матрицу;
- целочисленное время загрузки тестовой микропрограммы в бит-матрицу; -
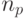 - разрядность гальванической
- разрядность гальванической 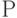 -шины;
-шины; -
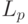 - "длина" тестовой микропрограммы, а
- "длина" тестовой микропрограммы, а 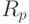 - разрядность регистра бит-инструкции.
- разрядность регистра бит-инструкции.
Вне зависимости от конструктивно-технологических особенностей построения тестовых интерфейсов минимальное время контроля дает полностью исправная бит-матрица, так как при этом не проводится адаптация тестовых микропрограмм под действующую карту отказов, которая позволяет нейтрализовать действие обнаруженных отказов и продолжить процесс диагностики. Поэтому первому варианту построения тестового интерфейса отвечает минимально минимальное время полного не Tlf -адаптивного контроля бит-матрицы Т -рекурсивными возвратными тестами. В соответствии с данными табл. 7.1 его можно записать:  , а и при
, а и при 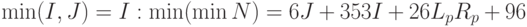 .
.
| Шаг | Функция |  |
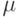 |
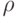 |
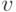 |
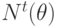 |
 |
 |
|---|---|---|---|---|---|---|---|---|
| 1 | P -шина | 1 | 1 | 4 | 1 |  |
 |
0 |
| 2 | D -шина | 2 | 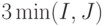 |
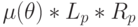 |
||||
| 3 | WTRh | 3 | 3 | 2 | 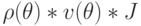 |
1 | ||
| WTRv | 4 | 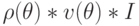 |
||||||
| 4 | AND | 5 | 3 | 4 | 5 |  |
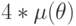 |
|
| XOR | 6 | |||||||
| ADD | 7 | |||||||
| ST1 | 8 | |||||||
| NAND | 9 | 4 | 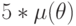 |
|||||
| CG | 10 | 3 | 1 | 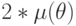 |
||||
| NOP | 11 | 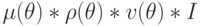 |
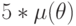 |
|||||
| Итого | 25 |  |
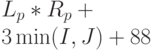 |
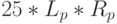 |
Отсюда, для платы СБИС Н1841 ВФ1, содержащей 30*88 бит-процессоров, или, что одно и то же, 6*22 СБИС, получим:
| Р -шина |  тактов тактов
|
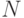 тактов тактов
|
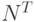 тактов тактов
|
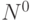 тактов
тактов
|
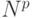 тактов
тактов
|
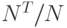
|

|
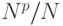
|
Отношение |
|---|---|---|---|---|---|---|---|---|---|
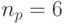 |
7040 | 194254 | 11036 | 7218 | 176000 | 0,057 | 0,037 | 0,906 | 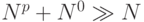 |
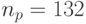 |
320 | 19534 | 11036 | 498 | 8000 | 0,565 | 0,025 | 0,410 |  |
где 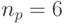 отвечает P -шине, обеспечивающей последовательный ввод микропрограммы во все СБИС одной строки, а
отвечает P -шине, обеспечивающей последовательный ввод микропрограммы во все СБИС одной строки, а 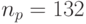 - в каждую СБИС независимо.
- в каждую СБИС независимо.
Из приведенных данных видно, что при такой организации тестового интерфейса решающий вклад во время диагностики полностью исправной бит-матрицы вносит время ввода тестовых микропрограмм, которое составляет 90 % от общего времени диагностики. Поэтому увеличение более чем в 20 раз разрядности P -шины снижает почти на порядок общее время диагностики и приводит к тому, что системообразующее неравенство (6.1) курса "Задачи и модели вычислительных наноструктур" начинает выполняться и для тестовых микропрограмм, правда, в ослабленном виде  .
.
Второму варианту построения тестового интерфейса отвечает табл. 7.2, согласно которой максимально минимальное время полного не Tlf -адаптивного контроля бит-матрицы Т -тестами имеет вид:
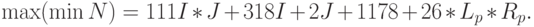
| Шаг | Функция |  |
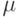 |
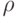 |
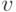 |
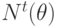 |
 |
 |
|---|---|---|---|---|---|---|---|---|
| 1 | P -шина | 1 | 1 | 4 | 1 |  |
 |
0 |
| 2 | D -шина | 2 | 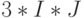 |
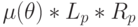 |
||||
| 3 | WTRh | 3 | 3 | 2 | 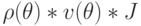 |
1 | ||
| WTRv | 4 | 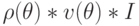 |
||||||
| 4 | AND | 5 | 3 | 4 | 5 | ![\mu(\theta)*
\rho(\theta)*
v(\theta)* [\lambda(\theta)(J-3) +3] + 12(\lambda(\theta)-
1)](/sites/default/files/tex_cache/ee38d6378bb13d939995a65e21988216.png) |
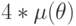 |
|
| XOR | 6 | |||||||
| ADD | 7 | |||||||
| ST1 | 8 | |||||||
| NAND | 9 | 4 | ![\mu(\theta)*
\rho(\theta)*
v(\theta)*
[\lambda(\theta)(J-5) +5] + 14(\lambda(\theta)-1)](/sites/default/files/tex_cache/808cef99c87efb046783a113a1f5c61b.png) |
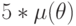 |
||||
| CG | 10 | 3 | 1 | ![\mu(\theta)*
\rho(\theta)*
v(\theta)*
[\lambda(\theta)(J-2) +2] + 12(\lambda(\theta)-1)](/sites/default/files/tex_cache/8868e176651370a2cc86917fcf937159.png) |
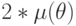 |
|||
| NOP | 11 | ![\mu(\theta)*
\rho(\theta)*
v(\theta)*
[\lambda(\theta)(J-2) +2] + 12(\lambda(\theta)-1)](/sites/default/files/tex_cache/8868e176651370a2cc86917fcf937159.png) |
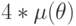 |
|||||
| Итого | 25 | 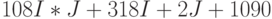 |
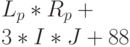 |
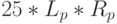 |
Здесь топология тестовых микропрограмм выбрана по критерию минимума неполноты покрытия бит-матрицы одноканальным U-образным функциональным тестом и в предположении: 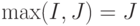 ;
; 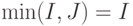 , причем
, причем ![\lambda(\theta) = ]min(I, J)/\mu(\theta)[](/sites/default/files/tex_cache/fcee51d7cae1dc0eafa60abd36d0ed5e.png) , где
, где ![][](/sites/default/files/tex_cache/426bab53a48fb39db26a30cc8dbaf53c.png) - старшее целое.
- старшее целое.
Отсюда, системообразующее неравенство (6.1) курса "Задачи и модели вычислительных наноструктур" стало выполняться и при малоразрядной P -шине, но не за счет снижения системных временных издержек, а за счет более чем 25-кратного увеличения продолжительности времени получения откликов от каждого бит-процессора U -образного тестового канала. При этом суммарное время контроля полностью исправной бит-матрицы возросло более чем в 2,5 раза.
Минимум миниморум времени контроля полностью исправной бит-матрицы обеспечивает тестовый интерфейс с непосредственным доступом к каждому бит-процессору матрицы по параллельным P - и D -шинам (табл. 7.3).
В этом случае только разрядности P - и D -шин зависят от размеров бит-матрицы, а все временные характеристики подсистемы локализации и идентификации отказов остаются неизменными для всех размеров контролируемой бит-матрицы:
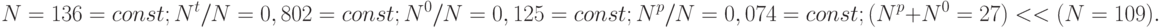
Для платы СБИС Н1841 ВФ1, содержащей 30*88 бит-процессоров, и 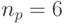 получим:
получим:
| Р -шина |  тактов тактов
|
 тактов тактов
|
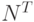 тактов тактов
|
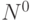 тактов
тактов
|
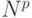 тактов тактов
|
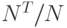
|

|
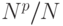
|
Отношение |
|---|---|---|---|---|---|---|---|---|---|
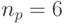 |
7040 | 476168 | 285120 | 15048 | 176000 | 0,599 | 0,032 | 0,370 |  |
| Шаг | Функция |  |
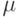 |
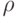 |
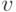 |
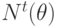 |
 |
 |
|---|---|---|---|---|---|---|---|---|
| 1 | Р-шина | 1 | 1 | 4 | 1 |  |
3 | 0 |
| 2 | D-шина | 1 | 1 | |||||
| 3 | WTRh | 3 | 2 | 2 | ||||
| WTRv | 4 | |||||||
| 4 | AND | 5 | 3 | 17 | 5 | 1 | ||
| XOR | 6 | |||||||
| ADD | 7 | |||||||
| ST1 | 8 | |||||||
| NAND | 9 | 4 | ||||||
| CG | 10 | 3 | 4 | 1 | ||||
| NOP | 11 | |||||||
| Итого | 109 |  |
17 | 10 |
Приведенные данные позволяют утверждать: продолжительность диагностики современных микроэлектронных МКМД-бит-процессорных матриц в основном определяется временем загрузки тестовых микропрограмм в бит-матрицу и временем получения индивидуальных откликов от всех бит-процессоров тестируемого канала, которые прямо или косвенно зависят от конструктивных характеристик бит-матрицы. К ним относятся: размеры 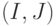 бит-матрицы, разрядность (
бит-матрицы, разрядность ( 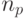 и
и 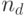 ) и конфигурация гальванических P - и D -шин, задающих длину
) и конфигурация гальванических P - и D -шин, задающих длину 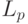 последовательной FIFO -регистровой P -шины и размеры 2-мерной, последовательной FIFO -регистровой D -шины (длину линейных или U -образных тестов).
последовательной FIFO -регистровой P -шины и размеры 2-мерной, последовательной FIFO -регистровой D -шины (длину линейных или U -образных тестов).
Для МКМД-бит-процессорных матриц на основе СБИС Н1841 ВФ1 локализация и идентификация отказов требует не менее  мс, но с увеличением тактовой частоты до 250 МГц и применением параллельной системы ввода микропрограмм рис. 7.19 это
время можно сократить в 80 раз, что становится приемлемым для периодического контроля бит-матрицы и подтверждения ее работоспособности в реальном времени.
мс, но с увеличением тактовой частоты до 250 МГц и применением параллельной системы ввода микропрограмм рис. 7.19 это
время можно сократить в 80 раз, что становится приемлемым для периодического контроля бит-матрицы и подтверждения ее работоспособности в реальном времени.
Необходимо помнить, что приведенные соотношения и полученные на их основе численные значения исходят из прямых временных затрат на диагностику МКМД-бит-процессорных матриц и они не учитывают системных временных издержек управляющей центральной БЦВМ, обеспечивающей заданную последовательность активизации тестовых микропрограмм, формирование и загрузку тест-данных, а также анализ полученных откликов. С учетом системных временных издержек центральной БЦВМ приведенные численные значения могут возрасти на порядок и более, так как исполняемые БЦВМ функции достаточно просты и значительно уступают по сложности задачам управления собственными ресурсами.
Другая центральная проблема проектирования устойчивых к отказам МКМД-бит-потоковых вычислителей - это задание или хотя бы описание катастрофической карты отказов, делающей бит-матрицу непригодной для решения возлагаемых на нее задач. Объективный критерий для такой оценки пока отсутствует. Более того, имеются признаки, указывающие, что дать такую оценку можно только в конкретных частных случаях, зависящих как от топологии отказов, так и от топологической схемы поток-оператора пользователя. Поэтому модельные исследования на этапе проектирования МКМД-бит-процессорных матричных СБИС должны быть направлены на то, чтобы определить важнейшие факторы, влияющие на формирование "катастрофической" карты отказов.
Очевидно: если остаточный аппаратный ресурс бит-матрицы не обеспечивает работоспособность простейших тестовых микропрограмм, то его явно недостаточно для обеспечения работоспособности более сложных микропрограмм пользователя. Поэтому уровень доступности бит-процессоров в матрице является одним из главных факторов появления "катастрофической" карты отказов.
Исследование доступности бит-процессоров матрицы проведено на основе гипотезы равномерного распределения отказов по матрице показали (рис. 7.24) и оно показало:
- уже при 30 % отказавших бит-процессоров начинает наблюдаться эффект исключения исправных бит-процессоров либо за счет сильного сужения путей доступа, либо за счет их полного отсутствия;
- при 50 % отказавших вообще наблюдается эффект доступности только периферийных процессоров.
Ориентированные на режим реального времени средства (микро) программной диагностики без особых проблем локализуют и идентифицируют карту до 15 одновременно сформированных отказов. При плавном нарастании карты эта величина достигает уже 20-30 отказов. Дальнейшее нарастание карты отказов приводит к доминированию эффекта "белых пятен", недоступных для тестирования в темпе реального времени.