|
"Теоретически канал с адресацией EUI 64 может соединить порядка запись вида ее можно заменить например на записи вида 264 или 1,8 * 1019
|
Адресация IPv6
Оценить необходимое число битов в адресе IPv6 нам позволит модель распределительной иерархии. Начнем мы с самого нижнего уровня в ней, который делить дальше нет смысла. Как мы знаем по опыту IPv4, субъект этого уровня — канал, а назначаемый ему префикс — подсеть. Иными словами, давайте допустим, что мы сохраним в IPv6 деление битов адреса на префикс подсети и номер узла в подсети.
Хотя каналу вполне можно назначить несколько подсетей, подсеть IP не может охватывать больше одного канала [§2.1 RFC 4291, RFC 4903]; это
один из фундаментальных постулатов TCP/IP. Какое максимальное число узлов способен соединить один канал? Разумная оценка здесь — это число
адресов MAC. Сегодня традиционные 48 битные адреса IEEE 802 уступают место 64 битным, т.н.
EUI-6411
Guidelines for 64-bit Global Identifier (EUI-64™) Registration Authority. IEEE. http://standards.ieee.org/regauth/oui/tutorials/EUI64.html
. Теоретически канал с адресацией EUI
64 может соединить порядка  узлов, так что пусть номер узла занимает для ровного счета 64 бита, то есть 8 байт.
узлов, так что пусть номер узла занимает для ровного счета 64 бита, то есть 8 байт.
Отлично, с номером узла мы разобрались. А какая длина потребуется префиксу подсети? Чтобы ответить и на этот вопрос, мы двинемся вверх по распределительной иерархии. Оставшаяся часть пирамиды носит скорее административный, нежели технический характер, и поэтому нам придется принять ее как данность. В ее современной структуре можно выделить четыре основных уровня12 http://www.ripe.net/docs/ipv6policy.html :
- конечный пользователь, например, организация или частный клиент;
- местная регистратура Internet — LIR (провайдер);
- региональная регистратура Internet — RIR;
- IANA.
Мы не поскупились, выдав 64 бита номеру узла, и теперь у нас возникает искушение продолжить оперировать порциями этой длины. Если мы так поступим, адрес получится длиною 320 бит, поскольку в нашей модели всего пять уровней иерархии: канал, пользователь, LIR, RIR и IANA. Безусловно, этого хватит на века, но по зубам ли будет столь длинный адрес современным вычислительным системам? Ведь пока длина адреса не превосходит разрядности вычислительной системы, элементарные операции над адресом можно выполнить, условно говоря, за единичное время. Иначе время операции начинает расти вместе с длиной адреса. Это справедливо как для традиционных ЭВМ с центральным процессором, так и для специализированных интегральных схем. Сегодня новые системы только-только подбираются к планке 256 бит13 Например, см. расширения SSE5 от AMD и AVX от Intel. ;так что давайте умерим нашу щедрость и посмотрим, нельзя ли будет обойтись более реальной величиной 128 бит.
Если весь адрес IPv6 окажется 128 битным, то на префикс подсети останется 64 бита. Допустим для первоначальной оценки, что это число битов
поровну делят между четырьмя уровнями пирамиды. Тогда каждый уровень сможет получить 16 бит: в сети конечного пользователя будет до 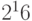 подсетей (по
подсетей (по  узлов каждая); у провайдера — до
узлов каждая); у провайдера — до 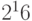 пользователей; каждая RIR сможет поддержать до
пользователей; каждая RIR сможет поддержать до 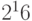 LIR;
наконец, IANA достанется
LIR;
наконец, IANA достанется 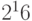 префиксов как для выделения их RIR, так и для служебных целей.
префиксов как для выделения их RIR, так и для служебных целей.
Чтобы почувствовать, насколько это много или мало — 16 бит на каждом уровне иерархии, — давайте переведем несколько примеров на доступный
нам язык IPv4. Так, если бы конечный пользователь назначал своим подсетям исключительно префиксы /24, то для выделения 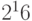 префиксов ему
понадобился бы блок /8 (или, по старинке, сеть класса A) — предел мечтаний любой корпорации. При этом одна подсеть была бы ограничена
всего лишь 254 узлами. В IPv6 же 16 бит на подсети — это минимум, что может получить пользователь, а в каждой его подсети будет до
префиксов ему
понадобился бы блок /8 (или, по старинке, сеть класса A) — предел мечтаний любой корпорации. При этом одна подсеть была бы ограничена
всего лишь 254 узлами. В IPv6 же 16 бит на подсети — это минимум, что может получить пользователь, а в каждой его подсети будет до  узлов! Что касается LIR, то до начала жесткой экономии адресов IPv4 новая LIR сразу получала блок /19, а он содержал всего лишь
узлов! Что касается LIR, то до начала жесткой экономии адресов IPv4 новая LIR сразу получала блок /19, а он содержал всего лишь 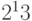 отдельных адресов, или же 32 подсети /24. Так что даже при делении префикса подсети IPv6 поровну LIR достанется втрое больше доступных
битов, чем было во времена IPv4. Выходит, даже 16 бит на уровень могло бы хватить.
отдельных адресов, или же 32 подсети /24. Так что даже при делении префикса подсети IPv6 поровну LIR достанется втрое больше доступных
битов, чем было во времена IPv4. Выходит, даже 16 бит на уровень могло бы хватить.
Конечно же, на практике число подчиненных субъектов будет расти при движении вниз. Так, IANA обслуживает всего несколько RIR, в ведении каждой RIR находится порядка сотен или тысяч LIR, а крупная LIR может поставлять услуги Internet миллионам конечных пользователей. Эту неравномерность шкалы вполне можно отразить в числе битов, которыми станет распоряжаться субъект каждого уровня, например, так:
- IANA — 8 бит (256 RIR и служебных префиксов);
- RIR — 16 бит (65 тысяч LIR);
- LIR — 24 бит (16 миллионов сетей-клиентов);
- конечный пользователь — 16 бит (65 тысяч подсетей).
Кроме того, основанное на префиксах распределение адресов позволяет варьировать размер блока в зависимости от запросов получателя, так что приведенные нами границы — лишь иллюстрация, а вовсе не строгое правило [§5 RFC 6177]. Небольшой LIR вполне хватит 16 бит, тогда как крупный корпоративный пользователь сможет получить у LIR в свое распоряжение, скажем, 24 бита и даже более того за счет слияния смежных 16 битных блоков. Тем не менее, ориентировочно в нашей модели конечный пользователь IPv6 получит от LIR префикс /48 и еще 16 бит останутся на внутреннюю структуру его сети.
В практике IPv6 уже есть прецеденты, когда особо крупная LIR получила у RIR /19 [§2.4.1 RFC 5375], что означает 29 доступных битов — конечно же, не считая тех битов, которые будут отданы в распоряжение конечных пользователей этой LIR. В терминах нашей оценочной модели, эта LIR сможет подключить до 229 пользователей, причем каждый получит довольно щедрую долю в адресном пространстве IPv6.
Чтобы выданный блок можно было укрупнить по требованию за счет слияния с соседним(и), достаточно следовать известной практике, когда
выдающая сторона вводит единичные биты не в младшие, а в старшие разряды префикса [RFC 1219, RFC 3531]. Например, распоряжаясь 4
битами, их значения следует выдавать не как 0, 1, 2, 3…, а как 0, 8, 4, 12, 2, 10, 6, 14… Тогда при доле заполнения до 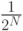 у
каждого выданного префикса заведомо будут свободны
у
каждого выданного префикса заведомо будут свободны 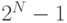 2N–1 префиксов, следующих за ним, и у всей группы N младших битов будут нулевые,
что обеспечит агрегирование. Например, пока выдано не более четверти доступных префиксов, каждый выданный блок можно укрупнить вдвое
или вчетверо. Мы предлагаем читателю самостоятельно разобраться с двоичной арифметикой этого полезного приема. (Подсказка: рассмотрите
"зеркальное отражение" n разрядной двоичной записи 0, 1, 2, 3…)
2N–1 префиксов, следующих за ним, и у всей группы N младших битов будут нулевые,
что обеспечит агрегирование. Например, пока выдано не более четверти доступных префиксов, каждый выданный блок можно укрупнить вдвое
или вчетверо. Мы предлагаем читателю самостоятельно разобраться с двоичной арифметикой этого полезного приема. (Подсказка: рассмотрите
"зеркальное отражение" n разрядной двоичной записи 0, 1, 2, 3…)
Таким образом, мы видим, что префикс подсети длиной 64 бита оставляет достаточно пространства для гибкого распределения битов согласно принципу: каждому по потребностям. Еще 64 бита мы заняли тем, что мы условно назвали номером узла в подсети. О структуре индивидуального адреса IPv6 мы еще поговорим в §2.6, а пока что сделаем наш первый технический вывод: всякий адрес IPv6 будет цепочкой из 128 битов [RFC 4291], как это показано на рис. 1.1.
Мы отложим численную интерпретацию этой цепочки до §2.2. Тем не менее, такая цепочка — несомненно, упорядочена: ее биты не "перетасованы", а следуют в строго определенном порядке.
Конечно, если бы IPv6 впервые возник в 2010 году, его адрес вполне мог бы удлиниться до 256 бит. Во-первых, это дало бы больше свободы в числе уровней распределения и маршрутизации. Во-вторых, разговоры об экономии префиксов14 Conservation. IPv6 Address Allocation and Assignment Policy. RIPE. http://www.ripe.net/docs/ipv6policy.html#conservation можно было бы отложить на неопределенный срок. С другой стороны, достаточное, но все же ограниченное число префиксов заставит инженера лишний раз подумать, а думать ему полезно. Избыток вычислительных ресурсов — это не оправдание бездумному их расходованию.
Любопытно заметить, что "ничто не ново под луной": завершенный 1 января 1983 года переход Internet от NCP к TCP/IP решал ту же самую задачу по расширению адресного пространства, а длина адреса тогда тоже увеличилась вчетверо, с одного байта до четырех.
Давайте оценим, сколько адресов IPv6 надо выдать, чтобы коэффициент HD (см. §1) достиг величины 0,8 (пороговое значение "пора задуматься" [§4 RFC 3194]). Нам будет удобно работать с двоичными логарифмами. Логарифм искомого числа примерно равен 0,8 * 128 102. То есть выходит, что "первый звонок" прозвенит за 26 двоичных порядков до абсолютного предела. В этом парадокс иерархического распределения: адреса фактически исчерпываются заметно раньше, чем можно было бы предвидеть на основании их общего числа.



 "
"