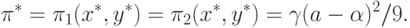Проблема эффективности свойств устойчивости и эффективности решений
Пример 1.2
( Дуополия3 Курно4 ).
Рассмотрим один из вариантов модели рынка однородного товара, согласно
которой на рынке действуют две фирмы P1 и P2,
предлагающие для продажи в рассматриваемом периоде соответственно q1 и q2 единиц указанного товара (который мы будем считать сколь угодно дробимым ). Таким образом, любое решение производителей P1 и P2, задаваемое парой q1,q2,
определяет общее количество товара
 |
(
3.5)
|
предлагаемого для продажи в данный период. Примем, что
клиринговая цена 
(т.е. цена, по которой осуществляются расчеты по
сделкам) зависит от количества поступившего на рынок товара и эта
зависимость определяется выражением
 |
(
3.6)
|
Замечание 1.10 (о выборе диапазона цен).
Как следует из (3.6), с ростом объема Q товара,
поступающего на рынок, цена p линейно убывает до нулевого
значения и остается на этой отметке при дальнейшем увеличении объемов поступлений.
Разумеется, что производители не будут расширять производство при падении
цен до нулевого уровня. Т.е. на любом реальном рынке заведомо выполняется
условие Q<a и, следовательно, графический образ
множества стратегических пар (q1,q2), которые могут
реализоваться, заведомо ограничен треугольником
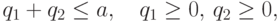 |
(
3.7)
|
изображенным жирными линиями на
рис.1.5.
Однако, если ограничить решения сторон парами
(q1,q2) из треугольника (3.7),
то возможности выбора одной стороны оказываются связанными с фактическим выбором, осуществленным
другой стороной. Это обстоятельство затрудняет непосредственное
использование введенных выше понятий равновесия по Нэшу и оптимальности по
Парето, поскольку их определения предполагают, что стороны независимы в
выборе своих стратегий.
Поэтому мы будем полагать, что определяемые сторонами P1 и P2 объемы предложения q1 и q2 могут соответствовать
любой точке (q1,q2) из квадранта (3.5). Т.е. мы принимаем, что множества X и Y стратегий сторон P1 и P2 есть
 |
(
3.8)
|
стратегий сторон, задаваемые условиями (3.8),
допускают использование произведения

в определениях равновесия по Нэшу и
оптимальности по Парето.
Примем, для простоты рассмотрения, что условия производства на обеих
фирмах являются одинаковыми и не предполагают постоянных затрат. Тогда
общие затраты Ci, осуществляемые фирмой Pi для
производства товара в количестве qi, определяются величиной
 |
(
3.9)
|
где
параметр c является константой (фактически, мы также
дополнительно предположили линейную зависимость затрат от объемов
выпуска).
Пусть  есть прибыль, получаемая фирмой Pi и
представляющая собой разность дохода этой фирмы и осуществленных ею
затрат (3.9). При сделанных предположениях зависимость прибыли (
есть прибыль, получаемая фирмой Pi и
представляющая собой разность дохода этой фирмы и осуществленных ею
затрат (3.9). При сделанных предположениях зависимость прибыли (  фирмы Pi от объемов выпуска обеих фирм, имеет вид
фирмы Pi от объемов выпуска обеих фирм, имеет вид
Отсюда (после подстановки (3.6)) получаем
выражение
 |
(
3.10)
|
которое в треугольнике (3.7) описывается более простой формулой
 |
(
3.11)
|
При этом согласно (3.11), в подобласти треугольника (3.7), описываемой условиями
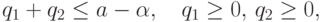 |
(
3.12)
|
является неотрицательной (см.
рис.1.5).
Соотношения (3.8) и (3.10) задают нормальную форму игры двух лиц, причем
выражения (3.10) для прибыли, получаемой
сторонами P1 и P2 в результате продажи товара,
играют роль критериев эффективности, в максимизации которых заинтересованы эти
стороны. Заметим, что интересы сторон в построенной игре являются
несовпадающими и не противоположными.
Исследуем вопрос о существовании устойчивых (по Нэшу) решений в
рассматриваемой игре. Определим условия, при которых достигается максимум
по qi от прибыли 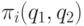 , получаемой
стороной Pi в предположении, что объем товара qj,
продаваемого другой стороной Pj
, получаемой
стороной Pi в предположении, что объем товара qj,
продаваемого другой стороной Pj 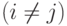 , является
фиксированным. С этой целью рассмотрим производную
, является
фиксированным. С этой целью рассмотрим производную
![\frac{d\pi_i(q_1,q_2)}{dq_i}=
\left\{\begin{aligned} & -c,&q_1+q_2>a,\\ &
\gamma\left[(a-\alpha)-2q_i-q_j\right],&q_1+q_2<a,\\
\end{aligned} \right.](/sites/default/files/tex_cache/53b45d16768c85540df8b5df450b1720.png) |
(
3.13)
|
которая определена в квадранте (3.5) всюду, кроме точек,
лежащих на
прямой q1+q2=a. Допустим, что
 |
(
3.14)
|
Тогда производная (3.13) имеет нулевые значения
во всех точках
прямой
 |
(
3.15)
|
лежащих в квадранте (3.5). При этом условие (3.14) выполняется во всех таких точках и,
кроме того,
вторая производная по
qi от прибыли
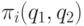
является отрицательной.
Таким образом, на отрезке прямой (3.15), соответствующей случаю i=1, j=2 и лежащей в первом квадранте (3.5),
достигается максимум прибыли стороны P1 (при
вариации объема выпуска q1 и фиксированном объеме q2 ).
Указанный отрезок нанесен на рис.1.6.
Отрезок, состоящий из точек максимума прибыли стороны P2 и соответствующий случаю i=2, j=1 также нанесен на рис.1.6.
При этом, согласно (3.11), прибыль  стороны Pi в точках (q1,q2), лежащих на прямой (3.15),
определяется выражением
стороны Pi в точках (q1,q2), лежащих на прямой (3.15),
определяется выражением
 |
(
3.16)
|
и, следовательно, растет с увеличением объема
qi. Указанные
направления роста прибыли вдоль отрезков прямых линий вида (3.15)
отмечены стрелками на рис.
рис.1.6.
Прямые линии (3.15), соответствующие случаям i=1, j=2 и i=2, j=1, пересекаются в точке с координатами
 |
(
3.17)
|
которая одновременно является точкой максимума прибыли
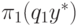
по
q1 и точкой максимума прибыли
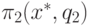
по
q2. Таким образом:
 |
(
3.18)
|
и, следовательно, точка

из (3.17)
есть
стратегическая точка равновесия.
При этом, согласно (3.16) и (3.17), уровень прибыли,
достижимый в точке равновесия, оказывается одинаковым для обеих сторон и
составляет величину
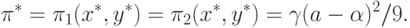 |
(
3.19)
|

 (т.е. цена, по которой осуществляются расчеты по
сделкам) зависит от количества поступившего на рынок товара и эта
зависимость определяется выражением
(т.е. цена, по которой осуществляются расчеты по
сделкам) зависит от количества поступившего на рынок товара и эта
зависимость определяется выражением
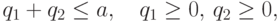

 в определениях равновесия по Нэшу и
оптимальности по Парето.
в определениях равновесия по Нэшу и
оптимальности по Парето.
 есть прибыль, получаемая фирмой Pi и
представляющая собой разность дохода этой фирмы и осуществленных ею
затрат (3.9). При сделанных предположениях зависимость прибыли (
есть прибыль, получаемая фирмой Pi и
представляющая собой разность дохода этой фирмы и осуществленных ею
затрат (3.9). При сделанных предположениях зависимость прибыли (  фирмы Pi от объемов выпуска обеих фирм, имеет вид
фирмы Pi от объемов выпуска обеих фирм, имеет вид


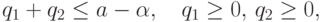
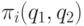 , получаемой
стороной Pi в предположении, что объем товара qj,
продаваемого другой стороной Pj
, получаемой
стороной Pi в предположении, что объем товара qj,
продаваемого другой стороной Pj 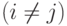 , является
фиксированным. С этой целью рассмотрим производную
, является
фиксированным. С этой целью рассмотрим производную![\frac{d\pi_i(q_1,q_2)}{dq_i}=
\left\{\begin{aligned} & -c,&q_1+q_2>a,\\ &
\gamma\left[(a-\alpha)-2q_i-q_j\right],&q_1+q_2<a,\\
\end{aligned} \right.](/sites/default/files/tex_cache/53b45d16768c85540df8b5df450b1720.png)


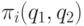 является отрицательной.
является отрицательной. стороны Pi в точках (q1,q2), лежащих на прямой (3.15),
определяется выражением
стороны Pi в точках (q1,q2), лежащих на прямой (3.15),
определяется выражением

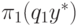 по q1 и точкой максимума прибыли
по q1 и точкой максимума прибыли 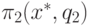 по q2. Таким образом:
по q2. Таким образом:
 из (3.17)
есть стратегическая точка равновесия.
При этом, согласно (3.16) и (3.17), уровень прибыли,
достижимый в точке равновесия, оказывается одинаковым для обеих сторон и
составляет величину
из (3.17)
есть стратегическая точка равновесия.
При этом, согласно (3.16) и (3.17), уровень прибыли,
достижимый в точке равновесия, оказывается одинаковым для обеих сторон и
составляет величину