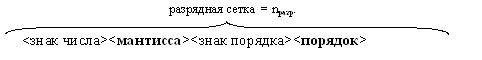Способы представления чисел в ЭВМ
Плавающая запятая
В ЭВМ с плавающей запятой число представляется в виде:
X = ± Mx * q±p,
где: Mx - мантисса числа;
q - основание системы счисления;
p - порядок.
Разрядная сетка машины принимает следующий вид:
Это лишь условное изображение основных слогов в числе. Заметим, что в реальной ЭВМ может быть принят любой другой порядок расположения.
Пусть " m " разрядов отведено под изображение мантиссы, а " k " разрядов под изображение порядка. Тогда для двоичной системы и нормализованного вида числа:
q = 2;
0,1 <= Mx < 1 - нормализованная мантисса.
То есть диапазон чисел:
Абсолютная ошибка представления числа в ЭВМ с плавающей запятой равна:
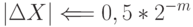
Так как
2-1 <= |Mx| <= 1-2-m,
то минимальная относительная ошибка:
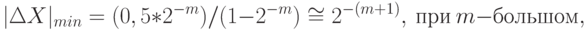
а максимальная относительная ошибка:
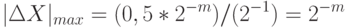
Видно, что относительная ошибка в ЭВМ с плавающей запятой не зависит от порядка числа. При этом точность представления больших и малых чисел изменяется незначительно.
Теоретически " плавающая запятая " имеет преимущества перед " фиксированной ". Но соответствующее устройство получается намного сложнее. К тому же специфика выполнения операций с плавающей запятой требует большего числа микроопераций, что приводит к снижению быстродействия ЭВМ. Однако " плавающая запятая " снимает с программиста обязанность отслеживать положение запятой в вычислениях и значительно упрощает сам процесс программирования вычислительных задач.