|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Оценивание
6.3. Асимптотика решений экстремальных статистических задач
Если проанализировать приведенные выше (см. 5.5) постановки и результаты, касающиеся эмпирических и теоретических средних и законов больших чисел, то становится очевидной возможность их обобщения. Так, доказательства теорем практически не меняются, если считать, что функция 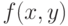 определена на декартовом произведении бикомпактных пространств
определена на декартовом произведении бикомпактных пространств  и
и  , а не на
, а не на 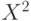 . Тогда можно считать, что элементы выборки лежат в
. Тогда можно считать, что элементы выборки лежат в 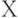 , а
, а  - пространство параметров, подлежащих оценке.
- пространство параметров, подлежащих оценке.
Обобщения законов больших чисел. Пусть, например, выборка  взята из распределения с плотностью
взята из распределения с плотностью 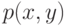 , где
, где  - неизвестный параметр. Если положить
- неизвестный параметр. Если положить



Соответственно законы больших чисел переходят в утверждения о состоятельности этих оценок в случае пространств  и
и  общего вида. При такой интерпретации функция
общего вида. При такой интерпретации функция 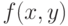 уже не является расстоянием или показателем различия. Однако для доказательства сходимости оценок к соответствующим значениям параметров это и не требуется. Достаточно непрерывности этой функции на декартовом произведении бикомпактных пространств
уже не является расстоянием или показателем различия. Однако для доказательства сходимости оценок к соответствующим значениям параметров это и не требуется. Достаточно непрерывности этой функции на декартовом произведении бикомпактных пространств  и
и  .
.
В случае функции 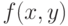 общего вида можно говорить об определении в пространствах произвольной природы оценок минимального контраста и их состоятельности. При этом при каждом конкретном значении параметра
общего вида можно говорить об определении в пространствах произвольной природы оценок минимального контраста и их состоятельности. При этом при каждом конкретном значении параметра  справедливо предельное соотношение
справедливо предельное соотношение
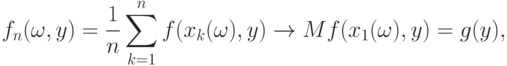
 - функция контраста. Тогда состоятельность оценок минимального контраста вытекает из справедливости предельного перехода
- функция контраста. Тогда состоятельность оценок минимального контраста вытекает из справедливости предельного перехода
Частными случаями оценок минимального контраста являются устойчивые (робастные) оценки Тьюки-Хубера (см. ниже), а также оценки параметров в задачах аппроксимации (параметрической регрессии) в пространствах произвольной природы.
Можно пойти и дальше в обобщении законов больших чисел. Пусть известно, что при каждом конкретном y при безграничном росте n имеет быть сходимость по вероятности

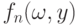 - последовательность случайных функций на пространстве
- последовательность случайных функций на пространстве  , а
, а 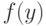 - некоторая функция на
- некоторая функция на  . В каких случаях и в каком смысле имеет место сходимость
. В каких случаях и в каком смысле имеет место сходимость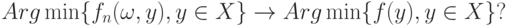
Другими словами, когда из поточечной сходимости функций вытекает сходимость точек минимума?
Причем под n здесь можно понимать натуральное число. А можно рассматривать сходимость по направленному множеству (см. 4.3), или же, что практически то же самое - "сходимость по фильтру" в смысле Картана и Бурбаки [ [ 4.11 ] , с.118]. В частности, можно описывать ситуацию вектором, координаты которого - объемы нескольких выборок, и все они безгранично растут. В классической математической статистике такие постановки рассматривать не любят.
Поскольку, как уже отмечалось, основные задачи прикладной статистики можно представить в виде оптимизационных, то ответ на поставленный вопрос о сходимости точек минимума дает возможность единообразного подхода к изучению асимптотики решений разнообразных экстремальных статистических задач. Одна из возможных формулировок, основанная на бикомпактности пространств  и
и  и нацеленная на изучение оценок минимального контраста, дана и обоснована выше. Другой подход развит в работе [
[
1.17
]
]. Он основан на использовании понятий асимптотической равномерной разбиваемости и координатной асимптотической равномерной разбиваемости пространств. С помощью указанных подходов удается стандартным образом обосновывать состоятельность оценок характеристик и параметров в основных задачах прикладной статистики.
и нацеленная на изучение оценок минимального контраста, дана и обоснована выше. Другой подход развит в работе [
[
1.17
]
]. Он основан на использовании понятий асимптотической равномерной разбиваемости и координатной асимптотической равномерной разбиваемости пространств. С помощью указанных подходов удается стандартным образом обосновывать состоятельность оценок характеристик и параметров в основных задачах прикладной статистики.
Рассматриваемую тематику можно развивать дальше, в частности, рассматривать аналоги законов больших чисел в случае пространств, не являющихся бикомпактными, а также изучать скорость сходимости 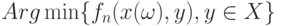 к
к  .
.
Приведем примеры применения результатов о предельном поведении точек минимума.
Задача аппроксимации зависимости (параметрической регрессии). Пусть  и
и  - некоторые пространства. Пусть имеются статистические данные -
- некоторые пространства. Пусть имеются статистические данные -  пар
пар 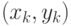 , где
, где 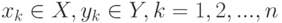 . Задано параметрическое пространство
. Задано параметрическое пространство  произвольной природы и семейство функций
произвольной природы и семейство функций 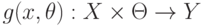 . Требуется подобрать параметр
. Требуется подобрать параметр 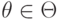 так, чтобы
так, чтобы 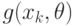 наилучшим образом приближали
наилучшим образом приближали  . Пусть
. Пусть  - последовательность показателей различия в
- последовательность показателей различия в  . При сделанных предположениях параметр
. При сделанных предположениях параметр  естественно оценивать путем решения экстремальной задачи:
естественно оценивать путем решения экстремальной задачи:
 |
( 1) |
Часто, но не всегда, все  совпадают. В классической постановке, когда
совпадают. В классической постановке, когда 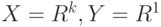 , функции
, функции  различны при неравноточных наблюдениях, например, когда число опытов меняется от одной точки
различны при неравноточных наблюдениях, например, когда число опытов меняется от одной точки  проведения опытов к другой.
проведения опытов к другой.
Если 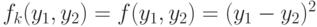 , то получаем общую постановку метода наименьших квадратов (см. подробности в
"Многомерный статистический анализ"
):
, то получаем общую постановку метода наименьших квадратов (см. подробности в
"Многомерный статистический анализ"
):

В рамках детерминированного анализа данных остается единственный теоретический вопрос - о существовании 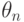 . Если все участвующие в формулировке задачи (1) функции непрерывны, а минимум берется по бикомпакту, то
. Если все участвующие в формулировке задачи (1) функции непрерывны, а минимум берется по бикомпакту, то 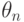 существует. Есть и иные условия существования
существует. Есть и иные условия существования 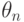 [
[
1.17
]
,
[
3.4
]
,
[
2.15
]
].
[
[
1.17
]
,
[
3.4
]
,
[
2.15
]
].
При появлении нового наблюдения  в соответствии с методологией восстановления зависимости рекомендуется выбирать оценку соответствующего
в соответствии с методологией восстановления зависимости рекомендуется выбирать оценку соответствующего  по правилу
по правилу

Обосновать такую рекомендацию в рамках детерминированного анализа данных невозможно. Это можно сделать только в вероятностной теории, равно как и изучить асимптотическое поведение 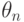 , доказать состоятельность этой оценки.
, доказать состоятельность этой оценки.
Как и в классическом случае, вероятностную теорию целесообразно строить для трех различных постановок.
- Переменная
 - детерминированная (например, время), переменная
- детерминированная (например, время), переменная  - случайная, ее распределение зависит от
- случайная, ее распределение зависит от  ;
; - Совокупность
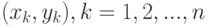 , - выборка из распределения случайного элемента со значениями в
, - выборка из распределения случайного элемента со значениями в  ;
; - Имеется детерминированный набор пар
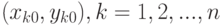 , результат наблюдения
, результат наблюдения 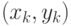 является случайным элементом, распределение которого зависит от
является случайным элементом, распределение которого зависит от 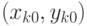 . Это - постановка конфлюэнтного анализа.
. Это - постановка конфлюэнтного анализа.
Во всех трех случаях
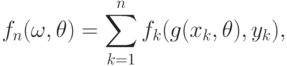
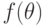 .
.Проще всего выглядит 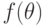 в случае второй постановки при
в случае второй постановки при 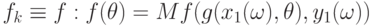 .
.
В случае первой постановки
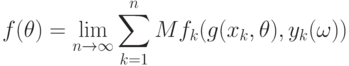
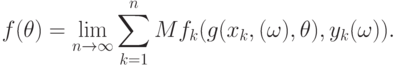
Во всех трех случаях на основе общих результатов о поведении решений экстремальных статистических задач можно изучить [ [ 1.17 ] , [ 3.4 ] , [ 2.15 ] ] асимптотику оценок ?n. При выполнении соответствующих внутриматематических условий регулярности оценки оказываются состоятельными, т.е. удается восстановить зависимость.
