|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Описание данных
5.1. Модели порождения данных
Детерминированный и модельно-вероятностный подходы. В прикладной статистике есть два подхода к исходным данным - детерминированный и модельно-вероятностный. В первом из них данные рассматриваются сами по себе, без попыток связать их с какой-либо более общей ситуацией. Например, при анализе данных о производственной деятельности конкретного предприятия за конкретный период времени подсчитывается процент брака по конкретным технологическим процессам, число работников на различных должностях, объем реализованной продукции по месяцам. К этой же категории данных относятся различные виды отчетности - бухгалтерская, налоговая, статистическая (для органов Росстата). Преимуществом детерминированного подхода является отсутствие каких-либо дополнительных предположений о данных. Недостаток состоит в невозможности обоснованного переноса выводов с конкретной ситуации на другие, ей аналогичные. Например, на другие периоды времени или на другие предприятия. При детерминированном подходе невозможно также оценить погрешность рассчитанных характеристик.
Чтобы выйти за пределы конкретной ситуации, необходимо использовать модельно-вероятностный подход, согласно которому основой алгоритмов расчетов является вероятностная модель порождения данных. При этом конкретные данные рассматриваются как реализации случайных величин, векторов, более общо - случайных элементов, т.е. как значения задающих их функций, определенных на вероятностном пространстве, в конкретной точке (элементарном событии 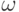 ).
).
Наиболее распространенная вероятностная модель порождения данных - это модель случайной выборки. Согласно этой модели данные 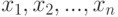 рассматриваются как реализации независимых одинаково распределенных случайных элементов (величин, векторов, множеств и других объектов нечисловой природы)
рассматриваются как реализации независимых одинаково распределенных случайных элементов (величин, векторов, множеств и других объектов нечисловой природы) 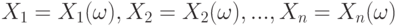 , т.е.
, т.е. 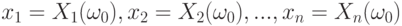 при некотором
при некотором 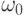 из пространства элементарных событий
из пространства элементарных событий  . Модель выборки обычно используется для описания результатов независимых наблюдений, измерений, анализов, опытов.
. Модель выборки обычно используется для описания результатов независимых наблюдений, измерений, анализов, опытов.
В некоторых случаях используют более специальные модели порождения данных. Например, при проведении испытаний на надежность используют план испытаний, согласно которому испытания прекращаются через время  . Это значит, что фиксируются только моменты отказа изделий, которые произошли до момента
. Это значит, что фиксируются только моменты отказа изделий, которые произошли до момента  . Пусть
. Пусть 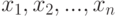 - наработки на отказ
- наработки на отказ  изделий. Статистику доступны только значения
изделий. Статистику доступны только значения 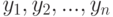 , где
, где  при
при  и
и  при
при  . Такая выборка, в которой часть описывающих реальное явление случайных величин заменена на граничное значение, называется цензурированной. Иногда используются и более сложные модели порождения данных.
Например, если аппаратурой не фиксируются значения, меньшие некоторого порога, то выборка не только цензурирована, но и состоит из случайного числа элементов. Бывают и процедуры, когда минимальный и максимальный элементы выборки отбрасываются, а остальные предоставляются статистику, и т.д.
. Такая выборка, в которой часть описывающих реальное явление случайных величин заменена на граничное значение, называется цензурированной. Иногда используются и более сложные модели порождения данных.
Например, если аппаратурой не фиксируются значения, меньшие некоторого порога, то выборка не только цензурирована, но и состоит из случайного числа элементов. Бывают и процедуры, когда минимальный и максимальный элементы выборки отбрасываются, а остальные предоставляются статистику, и т.д.
Параметрические и непараметрические модели случайной выборки. Рассмотрим ситуацию, когда элементы выборки - числа. Модель описывается функцией распределения элементов выборки. Можно ли что-либо сказать об этой функции?
В учебных курсах по теории вероятностей и математической статистике обычно рассматривают различные параметрические семейства распределений числовых случайных величин. А именно - изучают семейства нормальных распределений, логарифмически нормальных, экспоненциальных, гамма-распределений, распределений Вейбулла-Гнеденко и др. Все они зависят от одного, двух или трех параметров. Поэтому для полного описания распределения достаточно знать или оценить одно, два или три числа. Очень удобно. Поэтому широко развита и представлена в литературе параметрическая теория математической статистики, в которой предполагается, что распределения результатов наблюдений принадлежат тем или иным параметрическим семействам.
К сожалению, параметрические семейства существуют лишь в головах авторов учебников по теории вероятностей и математической статистике. В реальной жизни их нет. Поэтому прикладная статистика использует в основном непараметрические методы, в которых распределения результатов наблюдений могут иметь произвольный вид. В настоящем подразделе на примере нормального распределения подробно обсудим невозможность практического использования параметрических семейств для описания распределений конкретных данных.
В "Проверка гипотез" разобраны параметрические методы отбраковки резко выделяющихся наблюдений и продемонстрирована невозможность практического использования ряда методов параметрической статистики, ошибочность выводов, к которым они приводят. В "Статистический анализ числовых величин" рассмотрены непараметрические методы доверительного оценивания основных характеристик числовых случайных величин - математического ожидания, медианы, дисперсии, среднего квадратического отклонения, коэффициента вариации.
К настоящему времени непараметрические методы полностью покрывают область задач, которые ранее решались с помощью параметрической статистики. Поэтому можно порекомендовать использовать только непараметрическую статистику. Однако в литературе много внимания уделяется параметрическим методам, поэтому игнорировать в настоящем учебнике параметрическую статистику было признано нецелесообразным.
Часто ли распределение результатов наблюдений является нормальным? В эконометрических и экономико-математических моделях, применяемых, в частности, при изучении и оптимизации процессов маркетинга и менеджмента в целом, управления предприятием и регионом, точности и стабильности технологических процессов, в задачах надежности, обеспечения безопасности, в том числе экологической, функционирования технических устройств и объектов, разработки организационных схем часто применяют понятия и результаты теории вероятностей и математической статистики. При этом зачастую используют те или иные параметрические семейства распределений вероятностей. Наиболее популярно нормальное распределение. Используют также логарифмически нормальное распределение, экспоненциальное распределение, гамма-распределение, распределение Вейбулла-Гнеденко и т.д.
Очевидно, всегда необходимо проверять соответствие моделей реальности. Возникают два вопроса. Отличаются ли реальные распределения от используемых в модели? Насколько это отличие влияет на выводы?
Ниже на примере нормального распределения показано, что реальные распределения практически всегда отличаются от включенных в классические параметрические семейства. Имеющиеся отклонения от заданных семейств делают неверными выводы, основанные на использовании этих семейств. Например, выводы об отбраковке резко отличающихся наблюдений (выбросов).
Есть ли основания априори предполагать нормальность результатов измерений?
Иногда утверждают, что в случае, когда погрешность измерения (или иная случайная величина) определяется в результате совокупного действия многих малых факторов, то в силу центральной предельной теоремы (ЦПТ) теории вероятностей эта величина хорошо приближается (по распределению) нормальной случайной величиной. Такое утверждение справедливо, если малые факторы действуют аддитивно и независимо друг от друга. Если же они действуют мультипликативно, то в силу той же ЦПТ аппроксимировать надо логарифмически нормальным распределением. В прикладных задачах обосновать аддитивность, а не мультипликативность действия малых факторов обычно не удается. Если же зависимость имеет общий характер, не приводится к аддитивному или мультипликативному виду, а также нет оснований принимать модели, дающие экспоненциальное, Вейбулла-Гнеденко, гамма или иные распределения, то о распределении итоговой случайной величины практически ничего не известно, кроме внутриматематических свойств типа регулярности.
Экспериментальное изучение распределений погрешностей. При обработке конкретных данных иногда считают, что погрешности измерений имеют нормальное распределение. На предположении нормальности построены классические модели регрессионного, дисперсионного, факторного анализов, метрологические модели, которые еще продолжают встречаться как в отечественной ноpмативно-технической документации, так и в международных стандартах. На то же предположение опираются модели расчетов максимально достигаемых уровней тех или иных характеристик, применяемые при проектировании систем обеспечения безопасности функционирования экономических структур, технических устройств и объектов. Однако теоретических оснований для такого предположения нет. Необходимо экспериментально изучать распределения погрешностей.
Что же показывают результаты экспериментов? Сводка, данная в монографии [ [ 5.11 ] ], позволяет утверждать, что в большинстве случаев распределение погрешностей измерений отличается от нормального. Так, в Машинно-электротехническом институте (г. Варна в Болгарии) было исследовано распределение погрешностей градуировки шкал аналоговых электроизмерительных приборов. Изучались приборы, изготовленные в Чехословакии, СССР и Болгарии. Закон распределения погрешностей оказался одним и тем же. Он имеет плотность
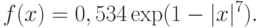
Были проанализированы данные о параметрах 219 фактических распределений погрешностей, исследованных разными авторами, при измерении как электрических, так и не электрических величин самыми разнообразными (электрическими) приборами. В результате этого исследования оказалось, что 111 распределений, т.е. примерно 50%, принадлежат классу распределений с плотностью
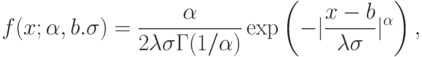
 - параметр степени (формы);
- параметр степени (формы);  - параметр сдвига;
- параметр сдвига; 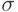 - параметр масштаба;
- параметр масштаба; 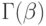 - гамма-функция от аргумента
- гамма-функция от аргумента  ;
;
В книге известного метролога проф. П. В. Новицкого [ [ 5.10 ] ] приведены результаты исследования законов распределения различного рода погрешностей измерения. Он изучил распределения погрешностей электромеханических приборов на кернах, электронных приборов для измерения температур и усилий, цифровых приборов с ручным уравновешиванием. Объем выборок экспериментальных данных для каждого экземпляра составлял 100-400 отсчетов. Оказалось, что 46 из 47 распределений значимо отличались от нормального. Исследована форма распределения погрешностей у 25 экземпляров цифровых вольтметров Щ-1411 в 10 точках диапазона. Результаты аналогичны. Дальнейшие сведения содержатся в монографии [ [ 5.11 ] ].
В лаборатории прикладной математики Тартуского государственного университета проанализировано 2500 выборок из архива реальных статистических данных. В 92% случаев гипотезу нормальности пришлось отвергнуть.
Приведенные описания экспериментальных данных показывают, что погрешности измерений в большинстве случаев имеют распределения, отличные от нормальных. Это означает, в частности, что большинство применений критерия Стьюдента, классического регрессионного анализа и других статистических методов, основанных на нормальной теории, строго говоря, не является обоснованным, поскольку неверна лежащая в их основе аксиома нормальности распределений соответствующих случайных величин.
Очевидно, для оправдания или обоснованного изменения существующей практики анализа статистических данных требуется изучить свойства процедур анализа данных при "незаконном" применении. Изучение процедур отбраковки показало, что они крайне неустойчивы к отклонениям от нормальности, а потому применять их для обработки реальных данных нецелесообразно (см. "Проверка гипотез" ); поэтому нельзя утверждать, что произвольно взятая процедура устойчива к отклонениям от нормальности.
Иногда предлагают перед применением, например, критерия Стьюдента однородности двух выборок проверять нормальность. Хотя для этого имеется много критериев, но проверка нормальности - более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистик типа Стьюдента, так и с помощью непараметрических критериев). Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. Так, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более, чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений. В большинстве экономических, технических, медико-биологических и других прикладных исследований число наблюдений существенно меньше. Особенно это справедливо для данных, используемых при изучении проблем, связанных с обеспечением безопасности функционирования экономических структур и технических объектов.
ЦПТ и нормальность. Иногда пытаются использовать ЦПТ для приближения распределения погрешности к нормальному, включая в технологическую схему измерительного прибора специальные сумматоры. Оценим полезность этой меры. Пусть  - независимые одинаково распределенные случайные величины с функцией распределения
- независимые одинаково распределенные случайные величины с функцией распределения 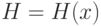 такие, что
такие, что  . Рассмотрим
. Рассмотрим
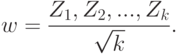
Показателем обеспечиваемой сумматором близости к нормальности является

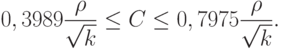
Правое неравенство в последнем соотношении вытекает из оценок константы в неравенстве Берри-Эссеена, полученном в книге [  , с.172], а левое - из примера в монографии [
, с.172], а левое - из примера в монографии [ 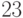 , с.140-141]. Для нормального закона
, с.140-141]. Для нормального закона 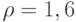 , для равномерного
, для равномерного 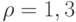 , для двухточечного
, для двухточечного  (это - нижняя граница для
(это - нижняя граница для 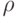 ). Следовательно, для обеспечения расстояния (в метрике Колмогорова) до нормального распределения не более 0,01 для "неудачных" распределений необходимо не менее
). Следовательно, для обеспечения расстояния (в метрике Колмогорова) до нормального распределения не более 0,01 для "неудачных" распределений необходимо не менее 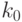 слагаемых, где
слагаемых, где
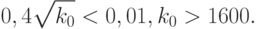
В обычно используемых сумматорах слагаемых значительно меньше.
Сужая класс возможных распределений 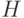 , можно получить, как показано в монографии [
[
5.6
]
], более быструю сходимость, но теория здесь еще не смыкается с практикой. Кроме того, не ясно, обеспечивает ли близость распределения к нормальному (в определенной метрике) также и близость распределений статистик. Речь идет о сравнении распределения статистики, построенной по случайным величинам, полученным суммированием, к распределению статистики, соответствующей нормальным результатам наблюдений. Видимо, для каждой конкретной статистики необходимы специальные теоретические исследования. Именно к такому выводу приходит автор монографии [
[
5.6
]
]. В задачах отбраковки выбросов ответ: "не обеспечивает" (см. ниже).
, можно получить, как показано в монографии [
[
5.6
]
], более быструю сходимость, но теория здесь еще не смыкается с практикой. Кроме того, не ясно, обеспечивает ли близость распределения к нормальному (в определенной метрике) также и близость распределений статистик. Речь идет о сравнении распределения статистики, построенной по случайным величинам, полученным суммированием, к распределению статистики, соответствующей нормальным результатам наблюдений. Видимо, для каждой конкретной статистики необходимы специальные теоретические исследования. Именно к такому выводу приходит автор монографии [
[
5.6
]
]. В задачах отбраковки выбросов ответ: "не обеспечивает" (см. ниже).
Отметим, что результат любого реального измерения записывается с помощью конечного числа десятичных знаков, обычно небольшого (2-5), так что любые реальные данные целесообразно моделировать лишь с помощью дискретных случайных величин, принимающих сравнительно небольшое число значений. Нормальное распределение - лишь аппроксимация реального распределения. Так, например, данные конкретного исследования, приведенные в работе [ [ 5.4 ] ], принимают значения от 1,0 до 2,2, т.е. всего 13 возможных значений. Из принципа Дирихле следует, что в какой-то точке построенная по данным работы [ [ 5.4 ] ] функция распределения отличается от ближайшей функции нормального распределения не менее чем на 1/26, т.е. на 0,04. Кроме того, очевидно, что для нормального распределения случайной величины вероятность попасть в дискретное множество десятичных чисел с заданным числом знаков после запятой равна 0.
Из сказанного выше следует, что результаты измерений и вообще статистические данные имеют свойства, приводящие к тому, что моделировать их следует случайными величинами с распределениями, более или менее отличными от нормальных. В большинстве случаев распределения существенно отличаются от нормальных. В других ситуациях нормальные распределения могут, видимо, рассматриваться как некоторая аппроксимация. Но никогда нет полного совпадения. Отсюда вытекает необходимость изучения свойств классических статистических процедур в неклассических вероятностных моделях (подобно тому, как это сделано в "Статистический анализ числовых величин" для критерия Стьюдента). А также целесообразность разработки устойчивых (учитывающих наличие отклонений от нормальности) и непараметрических, в том числе свободных от распределения процедур, их широкого внедрения в практику статистической обработки данных.
Опущенные здесь рассмотрения для других параметрических семейств приводят к аналогичным выводам. Итог можно сформулировать так. Распределения реальных данных практически никогда не входят в какое-либо конкретное параметрическое семейство. Реальные распределения всегда отличаются от тех, которые включены в параметрические семейства. Отличия могут быть большими или меньшими, но они всегда есть.
