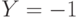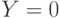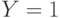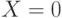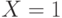Основы вероятностно-статистических методов описания неопределенностей

Некоторые постановки задач прикладной статистики, широко используемые в практической деятельности и в научных исследованиях. Чтобы дать представление о богатом содержании теории рассматриваемых методов, приведем краткий перечень основных типов постановок задач в соответствии с описанной выше классификацией областей прикладной статистики. Основные из них рассматриваются в дальнейших лекциях настоящего учебника.

1. Одномерная статистика.
   • Описание материала
     • Расчет выборочных характеристик распределения.
     • Построение гистограмм и полигонов частот.
     • Приближение эмпирических распределений с помощью распределений из системы Пирсона и других систем.
   • Оценивание.
     • Параметрическое оценивание.
       • Правила определения оценок и доверительных границ для параметров устойчивого распределения.
       • Правила определения оценок и доверительных границ для параметров логистического распределения.
       • Правила определения оценок и доверительных границ для параметров экспоненциального распределения и смеси экспоненциальных распределений (и так далее для различных семейств распределений).
     • Непараметрическое оценивание.
       • Непараметрическое точечное и доверительное оценивание основных характеристик распределения - математического ожидания, дисперсии, среднего квадратического отклонения, коэффициента вариации, квантилей, прежде всего медианы.
       • Непараметрические оценки плотности и функции распределения.
       • Непараметрическое оценивание параметра сдвига.
   • Проверка гипотез.
     • Параметрические задачи проверки гипотез.
       • Проверка равенства математических ожиданий для двух нормальных совокупностей.
       • Проверка равенства дисперсий для двух нормальных совокупностей.
       • Проверка равенства коэффициентов вариации для двух нормальных совокупностей.
       • Проверка равенства математических ожиданий и дисперсий для двух нормальных совокупностей.
       • Проверка равенства математического ожидания нормального распределения определенному значению.
       • Проверка равенства дисперсии нормального распределения определенному значению.
       • Проверка равенства параметров двух экспоненциальных совокупностей (и так далее - проверка утверждений о параметрах для различных семейств распределений).
     • Непараметрические задачи проверки гипотез.
       • Непараметрическая проверка равенства математических ожиданий для двух совокупностей.
       • Непараметрическая проверка равенства дисперсий для двух совокупностей.
       • Непараметрическая проверка равенства коэффициентов вариации для двух совокупностей.
       • Непараметрическая проверка равенства математических ожиданий и дисперсий для двух совокупностей.
       • Непараметрическая проверка равенства математического ожидания определенному значению.
       • Непараметрическая проверка равенства дисперсии определенному значению.
       • Проверка гипотезы согласия с равномерным распределением по критерию Колмогорова.
       • Проверка гипотезы согласия с равномерным распределением по критерию омега-квадрат (Крамера-Мизеса-Смирнова).
       • Проверка гипотезы согласия с равномерным распределением по критерию Смирнова.
       • Проверка гипотезы согласия с нормальным семейством распределений по критерию типа Колмогорова при известной дисперсии.
       • Проверка гипотезы согласия с нормальным семейством распределений по критерию типа Колмогорова при известном математическом ожидании.
       • Проверка гипотезы согласия с нормальным семейством распределений по критерию типа Колмогорова (оба параметра неизвестны).
       • Проверка гипотезы согласия с нормальным семейством распределений по критерию типа омега-квадрат при известной дисперсии.
       • Проверка гипотезы согласия с нормальным семейством распределений по критерию типа омега-квадрат при известном математическом ожидании.
       • Проверка гипотезы согласия с нормальным семейством распределений по критерию типа омега-квадрат (оба параметра неизвестны).
       • Проверка гипотезы согласия с экспоненциальным семейством распределений по критерию типа омега-квадрат ( и так далее для различных семейств распределений, тех или иных предположениях о параметрах, всевозможных критериев).
       • Проверка гипотезы однородности двух выборок методом Смирнова.
       • Проверка гипотезы однородности двух выборок методом омега-квадрат.
       • Проверка гипотезы однородности двух выборок с помощью критерия Вилкоксона.
       • Проверка гипотезы однородности двух выборок по критерию Ван-дер-Вардена.
       • Проверка гипотезы симметрии функции распределения относительно 0 методом Смирнова.
       • Проверка гипотезы симметрии функции распределения относительно 0 с помощью критерия типа омега-квадрат (Орлова).
       • Проверка гипотезы независимости элементов выборки.
       • Проверка гипотезы одинаковой распределенности элементов выборки (и т.д.).
2. Многомерный статистический анализ.
   • Описание материала.
     • Расчет выборочных характеристик (вектора средних, ковариационной и корреляционной матриц и др.).
     • Таблицы сопряженности.
     • Детерминированные методы приближения функциональной зависимости.
       • Метод наименьших квадратов.
       • Метод наименьших модулей
       • Сплайны и др.
     • Методы снижения размерности.
       • Алгоритмы факторного анализа.
       • Алгоритмы метода главных компонент
       • Алгоритмы многомерного метрического шкалирования.
       • Алгоритмы многомерного неметрического шкалирования.
       • Методы оптимального проецирования и др.
     • Методы классификации.
       • Методы кластер-анализа - иерархические процедуры.
       • Методы кластер-анализа - оптимизационный подход.
       • Методы кластер-анализа - итерационные процедуры
       • Методы группировки.
   • Оценивание.
     • Параметрическое оценивание.
       • Оценивание параметров многомерного нормального распределения.
       • Оценивание параметров в нормальной модели линейной регрессии.
       • Методы расщепления смесей.
       • Оценивание компонент дисперсии в дисперсионном анализе (в нормальной модели).
       • Оценивание размерности и структуры модели в регрессионном анализе (в нормальной модели).
       • Оценивание в дискриминантном анализе (в нормальной модели).
       • Оценивание в методах снижения размерности (в нормальной модели).
       • Нелинейная регрессия.
       • Методы планирования эксперимента.
     • Непараметрическое оценивание.
       • Непараметрические оценки многомерной плотности.
       • Непараметрическая регрессия (с погрешностями наблюдений произвольного вида).
       • Непараметрическая регрессия (на основе непараметрических оценок многомерной плотности).
       • Монотонная регрессия.
       • Непараметрический дискриминантный анализ.
       • Непараметрический дисперсионный анализ.
   • Проверка гипотез.
     • Параметрические задачи проверки гипотез.
       • Корреляционный анализ (нормальная модель).
       • Проверка гипотез об отличии коэффициентов при предикторах от 0 в линейной регрессии при справедливости нормальной модели.
       • Проверка гипотезы о равенстве математических ожиданий нормальных совокупностей (дисперсионный анализ).
       • Проверка гипотезы о совпадении двух линий регрессии (нормальная модель).
     • Непараметрические задачи проверки гипотез.
       • Непараметрический корреляционный анализ.
       • Проверка гипотез об отличии коэффициентов при предикторах от 0 в линейной регрессии (непараметрическая постановка).
       • Проверка гипотез в непараметрическом дисперсионном анализе.
       • Проверка гипотезы о совпадении двух линий регрессии (непараметрическая постановка).

Здесь остановимся, поскольку продолжение предполагало бы знакомство со многими достаточно сложными методами, о которых нет упоминаний в этом курсе. Приведенный выше перечень ряда основных типов постановок задач, используемых в прикладной статистике, дает первоначальное представление об объеме арсенала разработанных к настоящему времени интеллектуальных инструментов в рассматриваемой области.

Контрольные вопросы и задачи

1. Расскажите о понятиях случайного события и его вероятности.
2. Почему закон больших чисел и центральная предельная теорема занимают центральное место в вероятностно-статистических методах принятия решений?
3. Чем многомерный статистический анализ отличается от статистики объектов нечисловой природы?
4. Имеются три одинаковые с виду ящика. В первом белых шаров и черных; во втором белых и 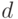черных; в третьем только белые шары. Некто подходит наугад к одному из ящиков и вынимает из него один шар. Найдите вероятность того, что этот шар белый.
5. Пассажир может воспользоваться трамваями двух маршрутов, следующих с интервалам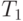и и соответственно. Пассажир может прийти на остановку в некоторый произвольный момент времени. Какой может быть вероятность того, что пассажир, пришедший на остановку, будет ждать не дольше , где ?
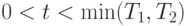6. Два стрелка, независимо один от другого, делают по два выстрела (каждый по своей мишени). Вероятность попадания в мишень при одном выстреле для первого стрелка - 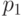, для второго - 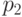. Выигравшим соревнование считается тот стрелок, в мишени которого будет больше пробоин. Найти вероятность того, что выиграет первый стрелок.
7. Полная колода карт (52 листа) делится наугад на две равные пачки по 26 листов. Найти вероятности следующих событий:
   • A - в каждой из пачек окажется по два туза;
   • B - в одной из пачек не будет ни одного туза, а в другой все четыре;
   • C - в одной из пачек будет один туз, а в другой три.
8. Случайная величина принимает значения 0 и 1, а случайная величина - значения (-1), 0 и 1. Вероятности 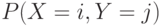задаются таблицей:

   	1/16	1/4	1/16
   	1/16	1/4	5/16

   Найдите распределение случайной величины 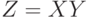, ее математическое ожидание и дисперсию.
9. В условиях задачи 8 найдите распределение случайной величины 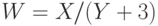, ее математическое ожидание и дисперсию.
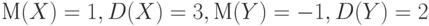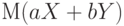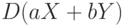10. Даны независимые случайные величины и такие, что . Найдите и , где .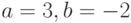

Темы докладов, рефератов, исследовательских работ

1. Описание данных с помощью гистограмм и непараметрических оценок плотности.
2. Сравнительный анализ методов оценивания параметров и характеристик.
3. Преимущества одношаговых оценок по сравнению с оценками метода максимального правдоподобия.
4. Непараметрический регрессионный анализ.
5. Аксиоматическое введение метрик и их использование в статистике объектов нечисловой природы.
6. Законы больших чисел в пространствах произвольной природы, в том числе в дискретных пространствах.
7. Оптимизационные постановки в вероятностно-статистических задачах принятия решений.