Самостоятельная работа 6: Распараллеливание программы вычисления определенного интеграла с помощью OpenMP
Распараллеливание программ с помощью OpenMP
Параллельная OpenMP-программа состоит из последовательных и параллельных секций. Границы параллельных секций обозначаются директивами OpenMP. Процесс разработки OpenMP-программы включает следующие этапы:
- Разработка последовательной программы.
- Выявление участков потенциального параллелизма. Чаще всего это циклы.
- Анализ трудоемкости параллельных секций (профилирование программы). Наибольший выигрыш в производительности дает распараллеливание секций, на которые приходятся наибольшие затраты процессорного времени.
- Пошаговое распараллеливание программы, начиная с наиболее трудоемких секций.
Профилирование может производиться как с помощью специальных программных инструментов, так и простыми средствами, например, с помощью вызова специальных подпрограмм-таймеров, размещенных в различных местах программы.
Цикл эффективно распараллеливается, если отсутствуют перекрестные зависимости между его итерациями. Избавиться от таких зависимостей иногда можно, выполнив преобразование цикла.
Необходимо правильно определить область видимости переменных в параллельных секциях программы. Параметр цикла, например, должен быть объявлен локальной переменной. Инвариант цикла (величина, не изменяющаяся при выполнении итераций цикла) должен быть глобальным.
При вычислении суммы, например, к переменной, которая используется для "накопления" суммы, должна быть применена операция приведения (редукции).
Следует обратить внимание на синхронизацию вычислений. По умолчанию в циклах используется барьерная синхронизация. Наличие синхронизаций увеличивает предсказуемость поведения программы, но замедляет ее работу.
Дополнительный выигрыш в производительности дает объединение нескольких параллельных секций в одну. В этом случае уменьшаются накладные расходы на запуск нитей и их завершение.
Трансляция OpenMP-программ
Трансляция OpenMP-программы выполняется со специальным ключом. В операционной системе Linux транслятор Intel®Compiler использует ключ –openmp, например:
#ifort –o my_prog prog_source.f90 -openmp
В операционной системе Microsoft®Windows командная строка выглядит следующим образом:
#ifort prog_source.f90 /Qopenmp
Приближенное вычисление определенного интеграла
Приближенное вычисление интеграла:
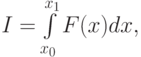
основано на его замене конечной суммой:
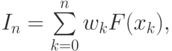
где 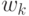 — числовые коэффициенты, а
— числовые коэффициенты, а 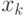 — точки отрезка
— точки отрезка
![[x_0, x_1]](/sites/default/files/tex_cache/ed145ada83ab2f2da15d2cea36777254.png) . Приближенное равенство:
. Приближенное равенство:
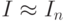
называется квадратурной формулой, точки 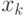 —
узлами квадратурной формулы, а числа
—
узлами квадратурной формулы, а числа
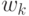 — коэффициентами квадратурной формулы.
Разные методы приближенного интегрирования отличаются выбором узлов и коэффициентов. От
этого выбора зависит погрешность квадратурной формулы:
— коэффициентами квадратурной формулы.
Разные методы приближенного интегрирования отличаются выбором узлов и коэффициентов. От
этого выбора зависит погрешность квадратурной формулы:
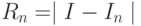
Метод трапеций
Интегрирование методом трапеций — основано на использовании
кусочно-линейного приближения для интегрируемой функции. Пусть 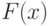 —
гладкая функция на интервале
—
гладкая функция на интервале ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) , и этот интервал делится на
, и этот интервал делится на  равных частей, каждая длиной
равных частей, каждая длиной 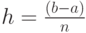 .
.
Приближение метода трапеций:
![I(h) = \frac {h[f_0+2f_1+2f_2+...+2f_{n-1}+2f_n]} {2}](/sites/default/files/tex_cache/8687bdbcdf30a5127b1d1a7597b3cda6.png)
где 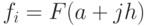 ,— значение интегрируемой функции в точке
,— значение интегрируемой функции в точке
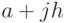 .
.
Метод Симпсона
Идея трехточечного метода Симпсона заключается в следующем.
Пусть 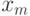 — это средняя точка интервала
— это средняя точка интервала ![[x_0, x_1]](/sites/default/files/tex_cache/ed145ada83ab2f2da15d2cea36777254.png) и пусть
и пусть 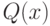 — единственный полином второй степени, который интерполирует (приближает) подынтегральную функцию
— единственный полином второй степени, который интерполирует (приближает) подынтегральную функцию
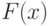 по точкам
по точкам  ,
, 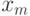 и
и  . Искомый
интеграл аппроксимируется интегралом от функции
. Искомый
интеграл аппроксимируется интегралом от функции 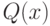 :
:
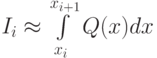
Эта оценка точна, если 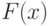 является полиномом степени 3.
является полиномом степени 3.
Обычно используются составные квадратурные формулы, когда промежуток
интегрирования разбивается на  подинтервалов и простая формула Симпсона
применяется на каждом из этих подинтервалов:
подинтервалов и простая формула Симпсона
применяется на каждом из этих подинтервалов:
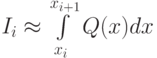
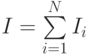
Недостатком рассмотренного метода является то, что он не дает возможности явно задать точность вычисления интеграла. Точность связана с количеством точек разбиения. От этого недостатка свободны методы интегрирования с адаптивным выбором шага разбиения. Если трехточечный метод Симпсона не дает достаточную точность на заданном интервале, он делится на 3 равные части и метод вновь применяется к каждой из полученных частей.
Лабораторная работа
В заданиях лабораторной работы 6 предлагается выполнить распараллеливание последовательных программ, предназначенных для вычисления определенных интегралов. В задании 4 распараллеливание производится с помощью MPI. Цель работы – получить навык анализа простых программ и выявления в них потенциального параллелизма, применить для распараллеливания OpenMP и MPI, сравнить трудоемкость обоих подходов и эффективность полученного результата. Звездочкой отмечено задание повышенной сложности.
Задания для практической работы
Задание 1
Получить у преподавателя файл с исходным текстом программы (примеры 1, 2) и ознакомиться с реализацией квадратурной формулы.
Задание 2
Откомпилировать программу, выполнить расчет. Определить процессорное время, потраченное на выполнение расчета.
Задание 3
Проанализировать последовательный код и выявить участки потенциального параллелизма. Выполнить распараллеливание с помощью OpenMP. Определить процессорное время, потраченное на выполнение расчета для разного числа потоков (меньшего, равного и большего, чем число процессоров). Сравнить с результатом, полученным в задании 2. Объяснить полученный результат.
Задание 4
Распараллелить программу с помощью MPI. Определить процессорное время, потраченное на выполнение расчета. Сравнить с результатами, полученными в заданиях 2 и 3.
Задание 5
На основании результатов, полученных при выполнении заданий данной лабораторной работы, написать отчет, в котором содержатся выводы об эффективности различных способов распараллеливания исходного последовательного кода и трудоемкости реализации этих способов на практике.
Пример 1
В программе на языке Fortran 90 реализован метод трапеций.
program integral_trapez
integer, parameter :: div_no = 100
real, parameter :: x0 = 0., x1 = 1. !3.14159
real, external :: F
real :: result
result = trapezium(F, x0, x1, div_no)
print *, result
end
real function trapezium(F, x0, x1, div_no)
real, external :: F
real, intent(in) :: x0, x1
integer, intent(in) :: div_no
real :: x, dx, sum
integer :: j
dx = (x1 - x0) / div_no
sum = F(x0) + F(x1)
x = x0
do j = 1, div_no - 1
x = x + dx
sum = sum + 2.0 * F(x)
end do
trapezium = dx * sum / 2.0
end
real function F(x)
real, intent(in) :: x
!F= sin(x)
F = 4./(1.+x**2)
end
Пример 2
В программе на языке Fortran 90 реализован метод Симпсона.
program integral_simps
integer, parameter :: div_no = 100
real, parameter :: x0 = 0., x1 = 1. !3.14159
real, external :: F
real :: result
result = simpson(F, x0, x1, div_no)
print *, result
end
real function simpson(F, x0, x1, div_no)
real, external :: F
real, intent(in) :: x0, x1
integer, intent(in) :: div_no
real :: x, dx, sum
integer :: j
dx = (x1 - x0) / (2.0 * div_no)
sum = F(x0) + F(x1)
x = x0
do j = 1, 2 * div_no - 1
x = x + dx
if (mod(j, 2) /= 0) then
sum = sum + 4.0 * F(x)
else
sum = sum + 2.0 * F(x)
end if
end do
simpson = dx * sum / 3.0
end
real function F(x)
real, intent(in) :: x
!F= sin(x)
F = 4./(1.+x**2)
end

