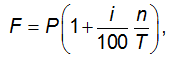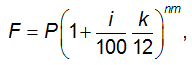НОУ ИНТУИТ | Экономика предприятия. Лекция 10: Финансы предприятий

Опубликован: 21.05.2017 | Доступ: свободный | Студентов: 1939 / 759 | Длительность: 14:29:00

Тема: Экономика

Специальности: Менеджер, Руководитель, Экономист, Бухгалтер

Контрольные задачи

Задача 6.1. Банк согласился учесть вексель на сумму 10 тыс. руб. за 60 дней до срока погашения. Определите сумму вексельного кредита, если ставка дисконта составляет 14% годовых.

Методические указания

Дисконтированную сумму вексельного кредита определяют по формуле

где	Р	-	начальная цена векселя, тыс. руб.;
	i	-	годовая ставка дисконта, %;
	n	-	время от момента приобретения до момента погашения векселя, дн.;
	Т	-	временнaя база (360 дней).

Задача 6.2. Определите сумму средств к погашению кредита в размере 2 тыс. руб., полученного на 30 дней под 16% годовых.

Методические указания

Наращенную сумму долга с учетом процентов за кредит рассчитывают по формуле

где	Р	-	сумма кредита, тыс. руб.;
	i	-	годовая ставка процента за кредит, %;
	п	-	срок, на который выдается кредит, дней;
	Т	-	временная база (360 дней).

Задача 6.3. Определите сумму вклада сегодня, чтобы через два года иметь накопления в размере 10 млн руб. Годовая ставка процента составляет 6%.

Методические указания

Дисконтированную сумму вклада вычисляют по формуле

где	Р	-	сумма вклада, млн руб.;
	i	-	годовая ставка процента, %;
	n	-	срок депозитного вклада, лет.

Задача 6.4. Банк принял к учету вексель в сумме 100 млн руб. за 60 дней до наступления срока погашения. Определите сумму вексельного кредита при годовой ставке дисконта 16%.

Методические указания

Дисконтированную сумму вексельного кредита определяют по формуле

где	P	-	начальная цена векселя, млн руб.;
	i	-	годовая ставка дисконта, %;
	n	-	время от момента приобретения до момента погашения векселя, дней;
	T	-	временная база (360 дней).

Задача 6.5. Используя формулу простых процентов, определите сумму средств к погашению краткосрочного кредита в размере 100 млн руб. через 30 дней. Годовая ставка процента составляет 16%.

Методические указания

Наращенную сумму долга с учетом процентов за кредит рассчитывают по формуле

где	Р	-	сумма кредита, млн руб.;
	i	-	годовая ставка процента за кредит, %;
	n	-	срок, на который выдается кредит, дней;
	T	-	временная база (360 дней).

Задача 6.6. Используя формулу сложных процентов, определите сумму депозитного вклада в размере 100 млн руб. через два года при ежегодном начислении 6% годовых.

Методические указания

Наращенную сумму депозитного вклада вычисляют по формуле

F = P (1 + i : 100)ⁿ,

где	Р	-	начальная сумма депозитного вклада, млн руб.;
	i	-	годовая ставка процента, %;
	n	-	срок депозитного вклада, лет.

Задача 6.7. Используя формулу сложных процентов, найдите сумму депозитного вклада в размере 100 млн руб. через два года при полугодовом начислении процентов. Годовая ставка составляет 6%.

Методические указания

Наращенную сумму депозитного вклада определяют по формуле

где	k	-	период времени, через который начисляются проценты, месяцев;
	n	-	срок депозитного вклада;
	m	-	частота начисления процентов.

Задача 6.8. Используя формулу дисконтирования, определите размер вексельного кредита при учете векселя в сумме 100 млн руб. за 100 дней до наступления срока погашения. Годовая ставка дисконта составляет 6%.

Методические указания

Дисконтированную сумму вексельного кредита рассчитывают по формуле

где	P	-	начальная цена векселя, млн руб.;
	i	-	годовая ставка дисконта, %;
	n	-	время от момента приобретения до момента погашения векселя, дней;
	T	-	временная база (360 дней).

Задача 6.9. Используя формулу дисконтирования, определите величину приведенного дохода от инвестиций за два года, если в первом году получено 100 млн руб., во втором — 200 млн руб. Годовая ставка дисконта составляет 16%.

Методические указания

Приведенный доход от инвестиций вычисляют по формуле

где	P_k	-	годовые денежные поступления в будущие периоды k, млн руб.;
	i	-	годовая ставка дисконта, доли единицы;
	k	-	номер периода;
	n	-	срок денежных поступлений, лет.

Задача 6.10. Определите сумму средств к погашению краткосрочного кредита в размере 100 млн руб. через 18 дней при годовой ставке процента 16%.

Методические указания

Наращенную сумму долга с учетом процентов за кредит определяют по формуле

где	P	-	сумма кредита, млн руб.;
	i	-	годовая ставка процента за кредит, %;
	n	-	срок, на который выдается кредит, дней;
	T	-	временная база (360 дней).

Задача 6.11. Определите сумму депозитного вклада в размере 100 млн руб. через два года при ежегодном начислении 10% годовых.

Методические указания

Наращенную сумму депозитного вклада рассчитывают по формуле

F = P (1 + i : 100)ⁿ,

где	Р	-	начальная сумма депозитного вклада, млн руб.;
	i	-	годовая ставка процента, %;
	n	-	срок депозитного вклада, лет.

Задача 6.12. Определите сумму депозитного вклада под 10% годовых в размере 100 млн руб. через два года при полугодовом начислении процентов.

Методические указания

Наращенную сумму депозитного вклада вычисляют по формуле

где	k	-	период времени, через который начисляются проценты, месяцев;
	n	-	частота начисления процентов;
	m	-	срок депозитного вклада, лет.

Задача 6.13. Распределению среди акционеров подлежит 20 млн руб. чистой прибыли предприятия. В обращении находится 1000 обыкновенных акций. Дивиденды, выплаченные по привилегированным акциям, составили 5 млн руб. Определите доход (прибыль) на одну акцию.

Методические указания

Доход на одну акцию определяют как частное от деления всей суммы денежных средств, направляемых на выплату дивидендов по обыкновенным акциям, на число акций, находящихся на руках акционеров:

Д = Д_об.а : Ч,

где	Д_об.а	-	дивиденды, выплачиваемые по обыкновенным акциям;
	Ч	-	число обыкновенных акций, находящихся в обращении;

Д_об.а = ЧП - Д_пр.а,

где	ЧП	-	чистая прибыль предприятия, подлежащая распределению среди акционеров;
	Д_пр.а	-	дивиденды, выплачиваемые по привилегированным акциям.

Задача 6.14. Предприятие выплатило по акциям 100 млн руб. дивидендов. Рыночная стоимость акций составляет 4 млрд руб. Определите текущую доходность (дивидендный доход) акций предприятия (в обращении находится 40 тыс. акций).

Контрольные задачи

Задача 7.1. Определите оптовую цену предприятия Ц_опт.пр, оптовую цену сбытовых организаций Ц_{опт.сб.орг}, государственную розничную цену Ц_р, если: плановая себестоимость единицы промышленной продукции С_пл = 150 тыс. руб.; прибыль, приходящаяся на единицу продукции, П_ед = 37,5 тыс. руб.; налог на добавленную стоимость НДС = 25,2 тыс. руб.; текущие издержки и прибыль сбытовых организаций ТЗ_сб + П_сб = 5,6 тыс. руб.; текущие издержки и прибыль торгующих организаций ТЗ_т + П_т = 11,7 тыс. руб.

Методические указания

Оптовая цена предприятия, руб.:

Ц_опт.пр = С + П + НДС.

Оптовая цена сбытовых организаций, руб.:

Ц_{опт.сб.орг} = Ц_опт.пр + П_сб + ТЗ_сб.

Государственная розничная цена, руб.:

Ц_р = Ц_{опт.сб.орг} + ТЗ_т + П_т.

Задача 7.2. Определите верхний предел цены нового оборудования, если: цена базисной модели Ц_б = 120 тыс. руб.; производительность базисной модели Q_б = 1000 шт./ч; производительность новой модели Q_н = 1000 шт./ч; норма амортизации базисной модели Н_а.б = 0,2; норма амортизации новой модели Н_а.н = 0,2; нормативный коэффициент эффективности Е_н = 0,25; эксплутационные издержки базисной модели И_б = 40 тыс. руб.; эксплутационные издержки новой модели И_н = 30 тыс. руб.; экономия капитальных вложений 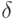$\black \delta$ К = 10 тыс. руб.

Методические указания

Верхний предел цены нового оборудования, руб.:

Ц_в = Ц_б x Q_н : Q_б (Н_а.б + Е_н) : (Н_а.н + Е_н) + (И_б - И_н) : (Н_а.н + Е_н) ± 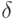$\black \delta$ К.

Дальше >>

Авторизоваться

Экономика предприятия

Финансы предприятий

Контрольные задачи

Контрольные задачи

Вопросы и ответы