Электронные платежные системы на основе цифровых денег
Уже достаточно давно банки и другие коммерческие структуры используют при проведении деловых операций электронный обмен данными EDI (Electronic Data Interchange) и электронный перевод денежных средств EFT (Electronic Funds Transfer). В современных платежных системах весь процесс от начала до конца происходит в электронной (цифровой) форме. При этом для обеспечения безопасности и признания законности (конфиденциальности пересылаемых электронных документов, аутентификации участников информационного обмена) повсеместно используются криптосистемы с открытым ключом для шифрования и формирования электронной подписи.
Учитывая, что традиционные денежные купюры суть не что иное как защищенный от подделки документ, логичным представляется переход к использованию цифровых денег. Защиту от подделки при этом может обеспечить электронная подпись банка, которая безусловно имеет большую надежность, чем традиционные водяные знаки, металлические полосы и т.п.
При осуществлении платежей с помощью популярной на западе кредитной карточки всегда, когда владелец карточки с ее помощью делает покупки, оплачивает налоги и т.д., где-то в базе данных делается отметка об этом событии. Соединив эти в отдельности малозначимые данные, можно собрать большое количество информации об отдельном человеке. При этом последний не в состоянии выяснить, кому и что известно о его частной жизни; не в состоянии управлять точностью этой информации или определять, кто может ее получать. Необходимо реализовать такую систему доступа к ресурсам и услугам, в которой одновременно с решением задач идентификации, аутентификации и авторизации клиента, обеспечивалась бы и анонимность последнего.
Обычные бумажные деньги отвечают всем этим свойствам. Если запрашиваемым ресурсом является какой-либо товар, то наличие у покупателя достаточного количества купюр является доказательством его права на доступ к ресурсу. Хотя каждая из купюр имеет уникальный номер, отслеживать купюры по номерам практически невозможно. Итак, проблема состоит в том, чтобы сделать электронные платежи в такой же степени анонимными, как и расчет с помощью обычных денег. Иначе говоря, возникает задача обеспечения неотслеживаемостиэлектронных документов и, в частности, электронных денег.
В этой главе представлено наиболее рациональное на сегодня решение для централизованных (online) платежных систем - технология цифровых денег или цифровой наличности, которая использует скорость и повсеместное распространение компьютерных сетей, при этом цифровые деньги сохраняют все свойства классических денег, основанных на общественном доверии (конфиденциальность и анонимность платежей, трудность подделки). Отличие цифровых денег от "обычных" заключается в том, что средства поддержки этой технологии являются "виртуальными", "ценности" хранятся в памяти компьютера (на жестком диске пользователя) или в микропроцессорной карте в форме алгоритмов.
Банк обменивает цифровые деньги на обычные после их проверки, используя информацию из специальной базы данных, которая может быть централизованной или распределенной. Обмен цифровыми деньгами между участниками осуществляется в реальном времени через сеть, финансовые расчеты с банком могут осуществляться не только в реальном времени.
Одна из особенностей системы цифровых денег по сравнению с другими (например, основанными на использовании кредитных карт) заключается в полной анонимности транзакций, не требующих от владельца купюры предъявления удостоверения личности, как это происходит в случае операций с физическими деньгами.[3GPP TR 21.905: Vocabulary for 3GPP Specifications.]
Рассмотрим основные криптографические алгоритмы, используемые при создании ЭПС на основе цифровых денег. Полная информация об используемых алгоритмах и протоколах содержится в "Методы защиты информации в компьютерных системах и сетях" .
8.1. Слепая электронная цифровая подпись
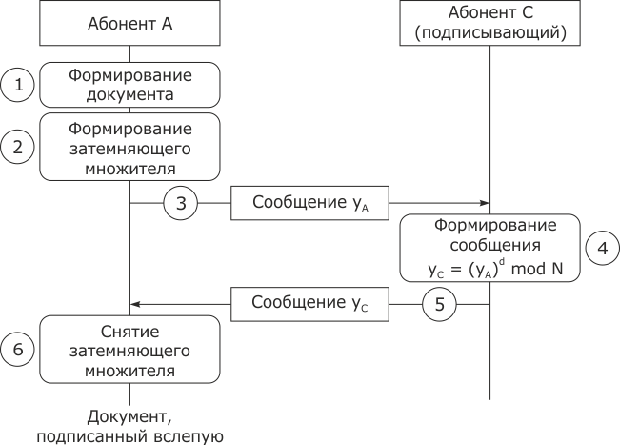
В протоколе слепой ЭЦП, представленной на рис. 8.1, принимают участие две стороны: абоненты А и C. Задачей абонента А является получить подпись абонента C на документе М, не раскрывая при этом содержимого документа М.
Схема слепой электронной подписи RSA
- Абонент А формирует документ М.
- Абонент А формирует случайное число R - затемняющий множитель, единственное требование к которому - существование обратного
 . Затем А шифрует затемняющий множитель на открытом ключе абонента С, умножает результат на M и посылает получившееся сообщение
абоненту C.
. Затем А шифрует затемняющий множитель на открытом ключе абонента С, умножает результат на M и посылает получившееся сообщение
абоненту C.
- Абонент С, получив сообщение
 ,подписывает его на своем секретном ключе и посылает сформированное сообщение
обратно абоненту А.
,подписывает его на своем секретном ключе и посылает сформированное сообщение
обратно абоненту А.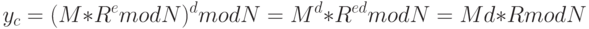
- Абонент А снимает действие затемняющего множителя, вычисляя
и получает в результате документ M, подписанный С, при этом абонент С ничего не узнал о содержимом подписанного им документа.

8.2. Цифровые наличные
Можно выделить следующие свойства, которыми должна обладать система цифровых наличных:
- трудоемкость подделки цифровых купюр;
- предотвращение возможности дублирования (с последующей повторной тратой) или оперативное его обнаружение;
- обеспечение анонимности покупателя;
- минимум операций с большими базами данных в режиме онлайн.
В системе цифровых наличных обычно можно выделить три протокола:
- протокол снятия со счета, позволяющий пользователю получать цифровые наличные у банка;
- платежный протокол, с помощью которого пользователь оплачивает покупки, обменивая их на цифровые купюры;
- депозитный протокол, позволяющий продавцу сдавать цифровые деньги в банк для перечисления средств на свой счет.
В информационном взаимодействии принимают участие трое:
- пользователь (будущий покупатель), применяющей цифровые наличные при осуществлении платежа;
- продавец, обменивающий некоторый товар на цифровые деньги;
- банк, выдающий цифровые наличные в обмен на обычные деньги, и наоборот.
Предположим, вышеупомянутые протоколы могут иметь следующий вид:
Протокол снятия со счета:
- пользователь сообщает банку, что он желает снять со своего счета некоторую сумму, например 100 дол.;
- банк в ответ на запрос отправляет цифровую купюру, имеющую следующий формат:
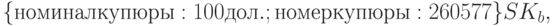
- пользователь проверяет подпись банка и если она верна принимает купюру.
Платежный протокол:
- пользователь оплачивает товар, предъявляя купюру;
- продавец проверяет подпись банка и, если она верна, принимает купюру в качестве платы.
Депозитный протокол:
- продавец пересылает купюру банку;
- банк проверяет свою подпись и, если она верна, начисляет на счет продавца сумму, равную номиналу купюры.
Описанные протоколы не решают проблемы, так как имеют следующие уязвимости:
- банк может связать имя пользователя с серийным номером купюры при ее выдаче и отслеживать все его действия;
- полученные от банка купюры можно дублировать и многократно использовать.
Анонимность покупателя обеспечивает применение слепой подписи в протоколе снятия со счета. Для предотвращения повторной траты банк должен поддерживать список номеров ранее потраченных купюр.
8.3. Строительные блоки
Деньги в форме бумажных купюр или металлических монет не требуют идентификации их владельца (покупателя или продавца), проверки его банковских реквизитов. Анонимность при выполнении удаленных транзакций зависит от двух факторов: возможности обмениваться анонимными сообщениями и возможности осуществлять анонимные платежи.
В системах цифровых денег предпринимаются действия для усиления конфиденциальности транзакций за счет анонимности и неотслеживаемости электронных платежей. Анонимность защищает личность участников (покупателя и продавца) после завершения транзакции. Неотслеживаемость означает, что два платежа одного индивидуума никаким образом не могут быть соотнесены друг с другом. Как следствие, банк (системный оператор) должен быть в состоянии модернизировать баланс счета для каждого участника без идентификации этого участника или соотнесения друг с другом различных транзакций, осуществляемых одним участником с любыми другими. Тем не менее каждый участник может разрешить системному оператору следить за денежными расчетами, чтобы гарантировать, например, платежи или доставку товара или выносить решения в случае возникновения разногласий.
Работа системы основывается на механизме слепой подписи, принципы которой были рассмотрены ранее. Подобный механизм позволяет плательщику самому "чеканить цифровые монеты", а банку "ставить печать" без получения информации о серийном номере монеты. При этом обмен сообщениями происходит с использованием обычных механизмов обеспечения конфиденциальности (шифрование с открытым ключом) и аутентичности (схема классической ЭЦП) информации. Эти механизмы были рассмотрены ранее, поэтому для простоты изложения в последующих разделах главы им не будет уделяться внимания.
8.3.1. Неотслеживаемость абонента А (дебитора)
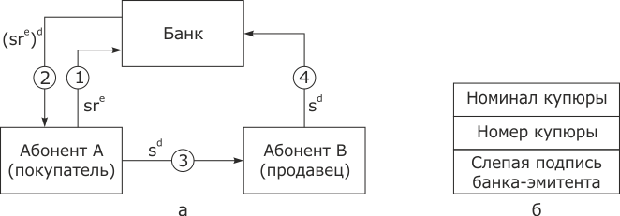
Процесс обеспечения неотслеживаемости платежа дебитора в виде схемы представлен на рис. 8.2.
увеличить изображение
Рис. 8.2. Цифровые деньги: а - простейшая схема обеспечения неотслеживаемости покупателя; б - цифровая купюра
Рассмотрим действия участника, желающего, чтобы банк подписал цифровую купюру вслепую. Банк имеет открытый ключ проверки подписи e, секретный ключ формирования подписи d, а также модуль N (N = pq, где p и q - различные простые числа) разрядностью 1024 или 2048 бит.
Шаг 1. Для получения цифровой купюры без разглашения ее серийного номера s, клиент А (дебитор) выбирает случайное число r, равномерно распределенное между 1 и (N – 1):
1 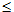 r
r 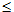 (N – 1).
(N – 1).
Только дебитор знает это число r, которое называется затемняющим множителем. Его роль заключается в том, чтобы скрыть серийный номер s купюры. Операция скрытия осуществляется путем умножения номера s на множитель r, зашифрованный на открытом ключе банка:
 .
.
Здесь и далее подразумевается, что все операции выполняются по модулю N.
Этот запрос пересылается банку ( рис. 8.2а).
В общем случае сообщение, посылаемое банку, состоит из нескольких полей, включая серийный номер s. Эти поля содержат, в частности, тип банковской операции, номер счета дебитора. Все эти поля подписываются с использованием секретного ключа дебитора, например:
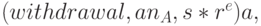
| где | withdrawal | - | операция снятия денег со счета; |
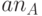 (account number A) (account number A) |
- | номер счета клиента; | |
| a | - | секретный ключ клиента. |
Соответствующий открытый ключ включается в сертификат, подписанный центром сертификации ключей.
Шаг 2. Банк заверяет купюру, подписывая полученное сообщение с использованием своего секретного ключа
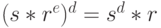
и возвращает ее абоненту А (дебитору). Затем банк снимает со счета дебитора сумму, соответствующую номиналу купюры.
Купюра анонимна, так как включает в себя только серийный номер, зашифрованный банковским секретным ключом. Банк знает только номер счета и, так как номер s затемнен, не в состоянии соотнести запрос продавца на перевод денежных средств после совершения факта покупки с конкретной цифровой купюрой, ранее вслепую им подписанной.
Абонент А получает полноценную цифровую купюру ( рис. 8.2б) путем деления числа, полученного от банка, на известный ему затемняющий множитель:
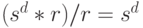 .
.
Используя банковский открытый ключ, дебитор проверяет соответствие полученной купюры, той, которая была послана на шаге 1, вычисляя
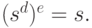
Шаг 3. Покупатель посылает подписанную купюру продавцу (абоненту В).
Шаг 4. Для перевода соответствующей суммы на свой счет (осуществления операции депозита) абонент В (продавец) посылает в банк следующее сообщение:
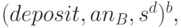
| где | deposit | - | операция перевода денег на счет; |
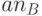 (account number B) (account number B) |
- | номер счета продавца; | |
| b | - | секретный ключ продавца. |
После проверки серийного номера купюры банк переводит эквивалентную сумму на счет продавца, изымает данную купюру из обращения, занося ее номер в список номеров купюр, изъятых из обращения. Банк может также послать расписку своему клиенту В в следующей форме:
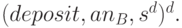
Банк поддерживает список номеров купюр, изъятых из обращения, для защиты от повторного предъявления одной и той же купюры при выполнении операции депозита.
8.3.2. Усиление защиты
В некоторых случаях клиент может быть заинтересован в потере неотслеживаемости для защиты своих прав (например, в случае спора с продавцом или кражи купюр). Формирование случайного числа r происходит путем применения хеш-функции к числу r`, который клиент держит в секрете. Предъявляя r` арбитру, дебитор может доказать, если это необходимо, что именно он владелец купюры, которую банк подписал вслепую. В отличие от продавца, который отказывается выполнять свои обязательства, или мошенника, укравшего купюру, которые не в состоянии сделать то же самое.
Подобным же образом может быть сформирован серийный номер s. Если s` есть случайное число, номер купюры s может быть получен так:
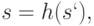
Дебитор должен предоставить прекурсор s` арбитру, чтобы доказать аутентичность купюры, которую продавец депонировал (положил в банк).
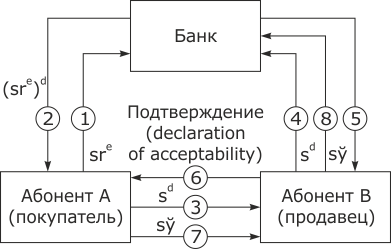
Использование прекурсора позволяет клиенту подтвердить банку, что он действительно является владельцем купюры. На рис. 8.3 приведена схема подобного подтверждения.
Шаг 5. Банк проверяет, что серийный номер купюры не содержится в списке ранее использованных купюр, и посылает продавцу заверение в законности сделки. Продавец пересылает это сообщение абоненту В (покупателю). Заверение о законности сделки включает в себя дату истечения срока действия купюры и может быть подписано с использованием секретного ключа банка, в результате и покупатель, и продавец могут удостовериться в целостности и подлинности этого сообщения.
Шаг 6. Абонент В пересылает полученное на предыдущем шаге заверение абоненту А.
Шаг 7. Если абонент А убедился в аутентичности заверения, он посылает прекурсор s` для банка абоненту В.
Шаг 8. Абонент В (продавец) проверяет прекурсор и посылает его в банк, который также убеждается в том, что именно s` использовался для получения s. В этом случае банк дает окончательное заключение о законности сделки, записывает купюру как депонированную, сохраняет копию прекурсора и переводит соответствующую сумму на счет продавца.
8.3.3. Неотслеживаемость абонента В (кредитора)
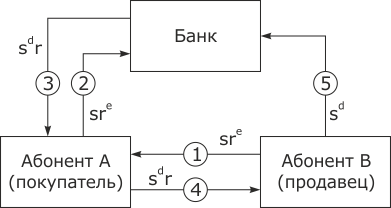
Процедура, необходимая для обеспечения неотслеживаемости кредитора, представлена на рис. 8.4.
Шаг 1. Для обеспечения собственной неотслеживаемости абонент В формирует "полуфабрикат" цифровой купюры  , затем посылает его абоненту А.
, затем посылает его абоненту А.
Шаг 2. Абонент А пересылает ее банку, чтобы тот поставил свою слепую подпись и снял соответствующую сумму со счета абонента В (кредитора).
Шаг 3. Подписав вслепую купюру, банк возвращает ее абоненту А.
Шаг 4. Абонент А пересылает ее абоненту В.
Шаг 5. Когда кредитор получает подписанную купюру, он использует открытый ключ банка, чтобы проверить, что данная купюра получена именно из того полуфабриката, который был ранее послан в банк:
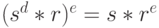 .
.
После удаления затемняющего множителя абонент В посылает купюру в банк. Банк переводит на счет В соответствующую сумму.
В результате банк не в состоянии выяснить, кто из участников - А или В - является инициатором информационного обмена.