Инструменты Gnumeric для статистиков
5.12 Две дисперсии: F-тест.
Этот инструмент позволяет проверить гипотезу о равенстве (или неравенстве) двух дисперсий. В качестве исходных данных будем использовать те же модельные выборки, что и в случае проверки гипотезы о равенстве двух средних.
В качестве первого примера рассмотрим 25 нормально распределенных случайных значений со средним значением 5 и стандартным отклонением 1 (Выборка1) и 25 нормально распределенных случайных значений со средним значением 7 и стандартным отклонением 1 (Выборка2). В этом случае дисперсии однозначно равны.
Результат проведения теста показан на рис. 5.45.
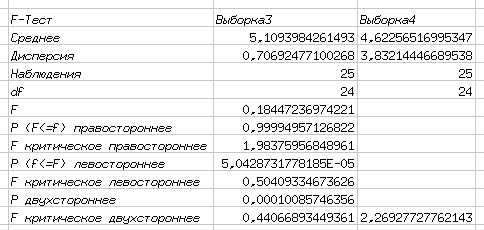
Теперь рассмотрим вариант, при котором дисперсии отличаются в два раза (Выборка3 и Выборка4). Результат теста показан на рис. 5.46.
Вывод получается следующий: чем сильнее отличаются дисперсии выборок, тем меньше значение  .
.
5.13 Оценка выживаемости (оценка Каплана-Майера)
Общие сведения о задаче анализа выживаемости можно получить в статье А.Б. Меркова "Об анализе выживаемости" или в руководствах по коммерческим статистическим пакетам (см. список литературы). Суть задачи заключается в том, чтобы по набору признаков (характеристик) определить время сохранения объектом этих характеристик ("время жизни") или распределение вероятностей сохранения характеристик в заданных пределах. Соответственно, можно строить прогнозы (предсказывать) среднее "время жизни" (время сохранения характеристик) таких объектов. Объектами могут быть вещества, устройства (приборы), сооружения и конструкции, а также живые существа. Чаще всего оценка выживаемости упоминается в связи с медицинской практикой.
В тех случаях, когда время наблюдения (продолжительность испытаний) меньше, чем "время жизни" конкретного объекта, получается, что "время жизни" точно не меньше времени наблюдения, а вот какое оно конкретно – узнать уже нельзя. Такие данные называются "цензурированными" (censored). Для группы объектов, участвующих в испытаниях возможны одновременно цензурированные и нецензурированные данные для различных экземпляров (например, при исследованиях срока службы энергосберегающих ламп в течение 10000 часов часть ламп вышла из строя в течение испытаний, а часть – так и не испортилась).
Пример использования Gnumeric для оценки выживаемости по Каплану-Майеру взят из справки по Gnumeric (Gnumeric 1.10.x).
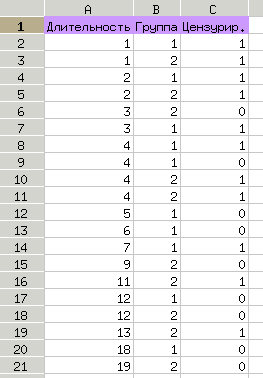
Заготовим исходные данные в соответствии с рис. 5.47.
Первый столбец ("Длительность") означает время испытаний (наблюдений) для каждого исследуемого экземпляра. В столбце "Группа" задаётся принадлежность объекта к группе объектов (группы могут отличаться местоположением, периодом времени наблюдений и другими признаками и обстоятельствами). В данном примере имеется только две группы. Наконец, в третьем столбце указывается признак "цензурированности" данных (если в ячейке 1 – данные цензурированы).
Все данные носят дискретный характер ("время жизни" изменяется дискретно).
Диалог настройки анализа вызывается через вложенное меню "Статистика/Зависимые наблюдения". Сначала определяется набор исходных данных и их цензурированность (вкладка "Ввод" диалога, рис. 5.48). Использование цензурированных данных разрешается включением соответствующего режима (Permit censorship).
На вкладке "Группы" задаётся количество групп и номера, которые их определяют. Теоретически можно объединять несколько групп в одну, указав диапазон номеров "от" и "до" (рис. 5.49). Для установки номера группы используются поля со счётчиками (для редактирования поля нужно дважды щёлкнуть в нём левой кнопкой мыши).
В этом примере (и по умолчанию) используется две группы, но с помощью кнопок "Добавить" и "Удалить" количество групп можно изменять так, как требуется.
На вкладке "Параметры" (рис. 5.50) определяется объём итоговой информации. Различные виды результатов можно включать и выключать. Пусть в рассматриваемом примере будет выводиться максимально полный набор результатов.
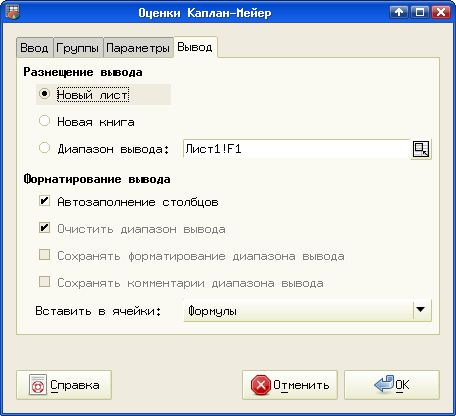
Наконец, на вкладке "Вывод" (рис. 5.51) имеет смысл выбрать вариант создания нового листа, поскольку количество выводимых результатов достаточно велико.
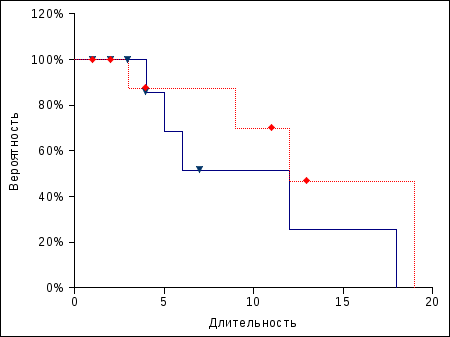
В результате получается график, на котором отмечены точки с цензурированными данными для обеих групп (рис. 5.52), а также выдаются численные результаты. На рис. 5.52 результаты для первой группы показаны сплошной линией, цензурированные точки – треугольниками, а результаты для второй группы – "точечной" линией, цензурированные точки – ромбы.
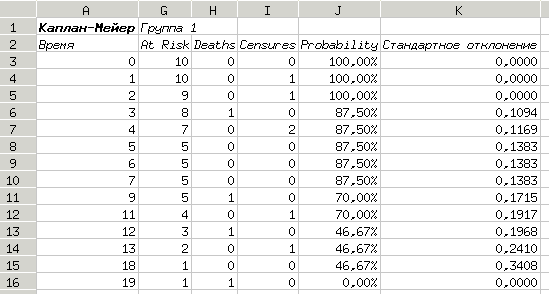
Численные результаты для первой группы показаны на рис. 5.53. Наличие деления на 0 при времени в 19 единиц, видимо, связано с тем, что для первой группы ("Группа0") нет нецензурированных данных для такого "времени жизни".
В следующих столбцах располагаются результаты для второй группы ("Группа1"). Для получения иллюстрации столбцы таблицы от  до
до  были скрыты (рис. 5.54).
были скрыты (рис. 5.54).
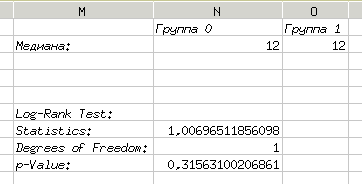
Наконец, общее сравнение среднего времени выживаемости в группах обеспечивается тестом Log-Rank (рис. 5.55).
Значение  позволяет оценить различие среднего времени жизни по группам. На основании полученной в рассматриваемом примере величины
позволяет оценить различие среднего времени жизни по группам. На основании полученной в рассматриваемом примере величины  делается вывод, что эти значения статистически неразличимы.
делается вывод, что эти значения статистически неразличимы.