|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Компания ALT Linux
Опубликован: 07.03.2015 | Доступ: свободный | Студентов: 2207 / 535 | Длительность: 24:14:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Лекция 3:
Операторы управления
3.6.3 Разветвляющийся процесс. Пересечение линий и решение уравнений.
Разработать программу на языке С++ для следующих заданий:
- Задан круг с центром в точке
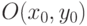 , радиусом
, радиусом 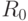 и точка
и точка 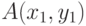 . Определить, находится ли точка внутри круга.
. Определить, находится ли точка внутри круга. - Задана окружность с центром в точке
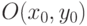 и радиусом
и радиусом 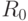 . Определить, пересекается ли заданная окружность с осью абсцисс, если пересекается — найти точки пересечения.
. Определить, пересекается ли заданная окружность с осью абсцисс, если пересекается — найти точки пересечения. - Задана окружность с центром в точке
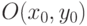 и радиусом
и радиусом 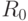 . Определить, пересекается ли заданная окружность с осью ординат, если пересекается — найти точки пересечения.
. Определить, пересекается ли заданная окружность с осью ординат, если пересекается — найти точки пересечения. - Задана окружность с центром в точке
 и радиусом
и радиусом 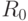 и прямая
и прямая 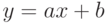 . Определить, пересекаются ли прямая и окружность. Если пересекаются, найти точки пересечения.
. Определить, пересекаются ли прямая и окружность. Если пересекаются, найти точки пересечения. - Заданы окружности. Первая с центром в точке
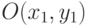 и радиусом
и радиусом 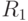 , вторая с центром в точке
, вторая с центром в точке 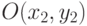 и радиусом
и радиусом 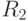 . Определить, пересекаются окружности, касаются или не пересекаются.
. Определить, пересекаются окружности, касаются или не пересекаются. - Заданы три точки
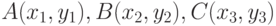 . Определить, какая из точек наиболее удалена от начала координат.
. Определить, какая из точек наиболее удалена от начала координат. - Заданы три точки
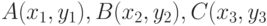 ). Определить, какая из точек
). Определить, какая из точек  или
или 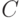 наименее удалена от точки
наименее удалена от точки  .
. - Определить, пересекаются ли линии
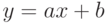 и
и 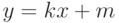 . Если пересекаются, найти точку пересечения.
. Если пересекаются, найти точку пересечения. - Определить, пересекает ли линия
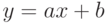 ось абсцисс. Если пересекает, найти точку пересечения.
ось абсцисс. Если пересекает, найти точку пересечения. - Определить, пересекаются ли линии
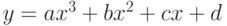 и
и 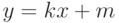 . Если пересекаются, найти точки пересечения.
. Если пересекаются, найти точки пересечения. - Определить, пересекаются ли линии
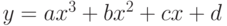 и
и  . Если пересекаются, найти точки пересечения.
. Если пересекаются, найти точки пересечения. - Определить, пересекаются ли линии
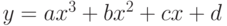 и
и 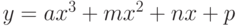 . Если пересекаются, найти точки пересечения.
. Если пересекаются, найти точки пересечения. - Определить, пересекаются ли линии
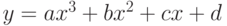 и
и 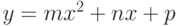 .Если пересекаются, найти точку пересечения.
.Если пересекаются, найти точку пересечения. - Определить, пересекает ли линия
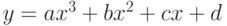 ось абсцисс. Если пересекает, найти точку пересечения.
ось абсцисс. Если пересекает, найти точку пересечения. - Определить, пересекаются ли параболы
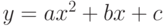 и
и  . Если пересекаются, то найти точки пересечения.
. Если пересекаются, то найти точки пересечения. - Определить, пересекаются ли линии
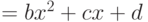 и
и 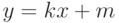 . Если пересекаются, найти точки пересечения.
. Если пересекаются, найти точки пересечения. - Найти точки пересечения линии
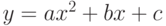 с осью абсцисс. Если линии не пересекаются выдать соответствующее сообщение.
с осью абсцисс. Если линии не пересекаются выдать соответствующее сообщение. - Определить, пересекаются ли линии
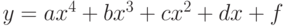 и
и 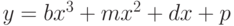 . Если пересекаются, найти точки пересечения.
. Если пересекаются, найти точки пересечения. - Определить, пересекаются ли линии
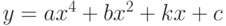 и
и 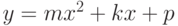 . Если пересекаются, найти точки пересечения.
. Если пересекаются, найти точки пересечения. - Определить, пересекает ли линия
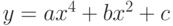 ось абсцисс. Если пересекает, найти точки пересечения.
ось абсцисс. Если пересекает, найти точки пересечения. - Найти комплексные корни уравнения
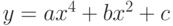 . Если в уравнении нет комплексных корней, вывести соответствующее сообщение.
. Если в уравнении нет комплексных корней, вывести соответствующее сообщение. - Найти комплексные корни уравнения
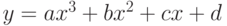 . Если в уравнении нет комплексных корней, вывести соответствующее сообщение.
. Если в уравнении нет комплексных корней, вывести соответствующее сообщение. - Найти комплексные корни уравнения
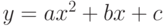 . Если в уравнении нет комплексных корней, вывести соответствующее сообщение.
. Если в уравнении нет комплексных корней, вывести соответствующее сообщение. - Заданы точки
 . Определить, какая из точек наименее удалена от начала координат.
. Определить, какая из точек наименее удалена от начала координат. - Даны координаты точки, не лежащей на координатных осях
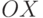 и
и 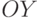 . Определить номер координатной четверти, в которой находится данная точка.
. Определить номер координатной четверти, в которой находится данная точка.
3.6.4 Циклический процесс. Вычисление значений функции
Разработать программу на языке С++. Для решения задачи использовать операторы for, while, do. Варианты заданий:
- Вывести на экран таблицу значений функции синус в диапазоне от
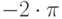 до
до 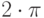 с шагом
с шагом  .
. - Вывести на экран таблицу квадратов первых десяти целых положительных чисел.
- Вывести на экран таблицу значений функции косинус в диапазоне от
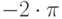 до
до 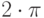 с шагом
с шагом  .
. - Вывести на экран таблицу кубов первых десяти целых положительных чисел.
- Вывести на экран таблицу значений квадратов синусов в диапазоне от
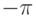 до
до 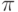 с шагом
с шагом  .
. - Вывести на экран таблицу значений квадратов косинусов в диапазоне от 0 до
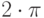 с шагом
с шагом  .
. - Вывести на экран таблицу квадратов первых десяти целых чётных положительных чисел.
- Вывести на экран таблицу квадратов первых десяти целых нечётных положительных чисел.
- Вывести на экран таблицу значений удвоенных синусов в диапазоне от
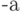 до
до  с шагом
с шагом  . Значения
. Значения  и
и  вводятся с клавиатуры.
вводятся с клавиатуры. - Вывести на экран таблицу значений удвоенных косинусов в диапазоне от
 до
до  с шагом
с шагом  . Значения
. Значения 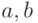 и
и  вводятся с клавиатуры.
вводятся с клавиатуры. - Вывести на экран таблицу кубов первых десяти целых нечётных положительных чисел.
- Вывести на экран таблицу кубов первых десяти целых чётных положительных чисел.
- Вывести на экран таблицу значений функции
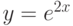 в диапазоне от
в диапазоне от 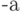 до
до  шагом
шагом  . Значения
. Значения  и
и  вводятся с клавиатуры.
вводятся с клавиатуры. - Вывести на экран таблицу значений функции
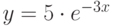 в диапазоне от
в диапазоне от  до
до  с шагом
с шагом  . Значения
. Значения 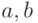 и
и  вводятся с клавиатуры.
вводятся с клавиатуры. - Вывести на экран таблицу квадратов первых десяти целых отрицательных чисел.
- Вывести на экран таблицу кубов первых десяти целых отрицательных чисел.
- Вывести на экран таблицу квадратных корней первых десяти целых положительных чисел.
- Вывести на экран таблицу кубических корней первых десяти целых положительных чисел.
- Вывести на экран таблицу значений функции
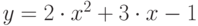 в диапазоне от
в диапазоне от 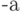 до
до  с шагом
с шагом  . Значения
. Значения 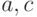 и
и  вводятся с клавиатуры.
вводятся с клавиатуры. - Вывести на экран таблицу значений функции
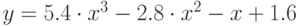 в диапазоне от
в диапазоне от  до
до  с шагом
с шагом  . Значения
. Значения 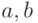 и
и  вводятся с клавиатуры.
вводятся с клавиатуры. - Вывести на экран таблицу квадратных корней первых десяти целых положительных чётных чисел.
- Вывести на экран таблицу квадратных корней первых десяти целых положительных нечётных чисел.
- Вывести на экран таблицу значений функции
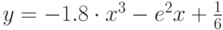 в диапазоне от -3 до 4 с шагом
в диапазоне от -3 до 4 с шагом  .
. - Вывести на экран таблицу значений функции y
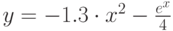 в диапазоне от -2 до 2 с шагом
в диапазоне от -2 до 2 с шагом  .
. - Вывести на экран таблицу степеней двойки в диапазоне от 0 до 10 с шагом 1.
3.6.5 Циклический процесс. Последовательности натуральных чисел
Разработать программу на языке С++ для следующих заданий:
- Дано целое положительное число
 . Вычислить сумму натуральных нечётных чисел не превышающих это число.
. Вычислить сумму натуральных нечётных чисел не превышающих это число. - Дано целое положительное число
 . Вычислить произведение натуральных чётных чисел не превышающих это число.
. Вычислить произведение натуральных чётных чисел не превышающих это число. - Дано целое положительное число
 . Вычислить количество натуральных чисел кратных трём и не превышающих число
. Вычислить количество натуральных чисел кратных трём и не превышающих число  .
. - Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 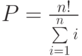 .
. - Вычислить количество натуральных двузначных чётных чисел не делящихся на 10.
- Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 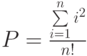 .
. - Вычислить сумму натуральных удвоенных чисел не превышающих 25.
- Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 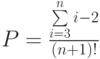 .
. - Дано целое положительное число
 . Вычислить сумму квадратов натуральных чётных чисел не превышающих это число.
. Вычислить сумму квадратов натуральных чётных чисел не превышающих это число. - Дано целое положительное число
 . Вычислить количество натуральных чисел кратных пяти и не превышающих число
. Вычислить количество натуральных чисел кратных пяти и не превышающих число  .
. - Определить значение выражения:
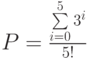 .
. - Дано целое положительное число
 . Вычислить сумму удвоенных натуральных нечётных чисел не превышающих это число.
. Вычислить сумму удвоенных натуральных нечётных чисел не превышающих это число. - Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 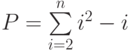 .
. - Найти сумму нечётных степеней двойки. Значение степени изменяется от 1 до 9.
- Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 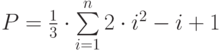 .
. - Дано целое положительное число
 . Вычислить произведение натуральных чисел кратных трём и не превышающих число
. Вычислить произведение натуральных чисел кратных трём и не превышающих число  .
. - Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 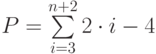 .
. - Вычислить сумму натуральных трёхзначных чисел кратных пяти и не делящихся на десять.
- Определить значение выражения:
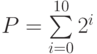 .
. - Вычислить количество натуральных двузначных нечётных чисел не делящихся на 5.
- Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 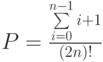 .
. - Задано целое положительное число
 . Определить значение выражения:
. Определить значение выражения: 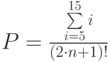 .
. - Найти произведение чётных степеней двойки. Значение степени изменяется от 0 до 8.
- Вычислить произведение натуральных чисел не превышающих 15.
- Вычислить произведение натуральных двузначных чисел кратных трём и не делящихся на 10.
3.6.6 Циклический процесс. Последовательности произвольных чисел
Разработать программу на языке С++ для следующих заданий:
- Вводится последовательность ненулевых чисел, 0 — конец последовательности. Определить сумму положительных элементов последовательности.
- Вычислить сумму отрицательных элементов последовательности из
 произвольных чисел.
произвольных чисел. - Вводится последовательность ненулевых чисел, 0 — конец последовательности. Определить, сколько раз последовательность поменяет знак.
- В последовательности из
 произвольных чисел подсчитать количество нулей.
произвольных чисел подсчитать количество нулей. - Вводится последовательность ненулевых чисел, 0 — конец последовательности. Определить наибольшее число в последовательности.
- Вводится последовательность из
 произвольных чисел найти наименьшее число в последовательности.
произвольных чисел найти наименьшее число в последовательности. - Вводится последовательность ненулевых чисел, 0 — конец последовательности. Определить среднее значение элементов последовательности.
- Вводится последовательность из
 произвольных чисел, найти среднее значение положительных элементов последовательности.
произвольных чисел, найти среднее значение положительных элементов последовательности. - Вводится последовательность ненулевых чисел, 0 — конец последовательности. Подсчитать процент положительных и отрицательных чисел.
- Вводится последовательность из
 произвольных чисел. Определить процент положительных, отрицательных и нулевых элементов.
произвольных чисел. Определить процент положительных, отрицательных и нулевых элементов. - Вводится последовательность из
 произвольных чисел. Вычислить разность между наименьшим и наибольшим значениями последовательности.
произвольных чисел. Вычислить разность между наименьшим и наибольшим значениями последовательности. - Вводится последовательность из
 положительных целых чисел. Найти наименьшее число среди чётных элементов последовательности.
положительных целых чисел. Найти наименьшее число среди чётных элементов последовательности. - Вводится последовательность из
 целых чисел. Определить, является ли эта последовательность знакочередующейся.
целых чисел. Определить, является ли эта последовательность знакочередующейся. - Определить, является ли последовательность из
 произвольных чисел строго возрастающей (каждый следующий элемент больше предыдущего).
произвольных чисел строго возрастающей (каждый следующий элемент больше предыдущего). - Вводится последовательность произвольных чисел, 0 — конец последовательности. Определить, является ли эта последовательность строго убывающей (каждый следующий элемент меньше предыдущего).
- Вводится последовательность ненулевых целых чисел, 0 — конец последовательности. Определить среднее значение чётных элементов последовательности.
- Вводится последовательность из
 произвольных чисел, найти среднее значение отрицательных элементов последовательности.
произвольных чисел, найти среднее значение отрицательных элементов последовательности. - В последовательности из
 целых чисел подсчитать количество чётных и нечётных чисел.
целых чисел подсчитать количество чётных и нечётных чисел. - Вводится последовательность целых чисел, 0 — конец последовательности. Определить процент чётных и нечётных чисел в последовательности.
- Вводится последовательность из
 целых чисел. Определить, содержит ли последовательность хотя бы два соседних одинаковых числа.
целых чисел. Определить, содержит ли последовательность хотя бы два соседних одинаковых числа. - Вводится последовательность целых чисел, 0 — конец последовательности. Определить наибольшее число среди нечётных элементов последовательности.
- Вводится последовательность произвольных чисел, 0 — конец последовательности. Определить сумму и количество чисел в последовательности.
- Вводится последовательность из
 произвольных чисел. Найти сумму положительных и сумму отрицательных элементов последовательности.
произвольных чисел. Найти сумму положительных и сумму отрицательных элементов последовательности. - Вводится последовательность произвольных чисел, 0 — конец последовательности. Определить отношение минимального и максимального элементов друг к другу.
- Вводится последовательность из
 целых чисел. Определить количество одинаковых рядом стоящих чисел.
целых чисел. Определить количество одинаковых рядом стоящих чисел.
3.6.7 Циклический процесс. Работа с цифрами в числе
Разработать программу на языке С++ для следующих заданий:
- Определить, является ли целое положительное число совершённым. Совершённое число равно сумме всех своих делителей, не превосходящих это число. Например, 6=1+2+3 или 28=1+2+4+7+14.
- Проверить, является ли пара целых положительных чисел дружественными. Два различных натуральных числа являются дружественными, если сумма всех делителей первого числа (кроме самого числа) равна второму числу. Например, 220 и 284, 1184 и 1210, 2620 и 2924, 5020 и 5564.
- Определить, является ли целое положительное число недостаточным. Недостаточное число всегда больше суммы всех своих делителей за исключением самого числа.
- Вводится целое положительное число. Определить количество чётных и нечётных цифр в числе.
- Вводится целое положительное число. Найти число, которое равно сумме кубов цифр исходного числа.
- Вводится целое положительное число. Определить, совпадает ли сумма цифр, расположенных до середины числа, с суммой цифр расположенных после. Например, задано число из восьми цифр 12112021. Здесь, сумма первых четырёх цифр, равна сумме следующих четырёх цифр 1 + 2 + 1 + 1 = 2+0+2+1 = 5. Или, задано число из семи цифр 3456444, тогда 3+4+5 = 4 + 4 + 4 = 12. Здесь цифра 6 не учитывается.
- Вводится целое положительное число. Найти суммы чётных и нечётных цифр заданного числа.
- Задано целое положительное число. Определить количество его чётных и нечётных делителей.
- Проверить, являются ли два целых положительных числа взаимно простыми. Два различных натуральных числа являются взаимно простыми, если их наибольший общий делитель равен единице.
- Определить, является ли целое положительное число составным. Составное число имеет более двух делителей, то есть не является простым.
- Вводится целое положительное число. Найти наименьшую цифру числа.
- Задано целое положительное число. Определить, является ли оно числом Армстронга. Число Армстронга — натуральное число, которое равно сумме своих цифр, возведённых в степень, равную количеству его цифр. Например, десятичное число 153 — число Армстронга, потому что: 13 + 33 + 53 = 1 + 27 + 125 = 153.
- Вводится целое положительное число. Найти произведение всех ненулевых цифр числа.
- Вводится целое положительное число. Найти наибольшую цифру числа.
- Вводится целое положительное число. Определить позицию наибольшей цифры в числе.
- Вводится целое положительное число. Найти число, которое равно сумме удвоенных цифр исходного числа.
- Вводится целое положительное число. Найти число, которое равно сумме квадратов цифр исходного числа.
- Задано целое положительное число. Определить сумму его делителей.
- Вводится целое положительное число. Определить позицию наименьшей цифры в числе.
- Проверить, что два целых положительных числа не являются взаимно простыми. Различные натуральные числа не являются взаимно простыми, если их наибольший общий делитель отличен от единицы.
- Убедиться, что заданное целое положительное число не является палиндромом. Числа-палиндромы симметричны относительно своей середины, например, 12021 или 454.
- Убедиться, что заданное целое положительное число не является совершённым. Совершённое число равно сумме всех своих делителей, не превосходящих это число. Например, 6=1+2+3 или 28=1+2+4+7+14.
- Проверить, что два целых положительных числа не являются дружественными. Два различных натуральных числа являются дружественными, если сумма всех делителей первого числа (кроме самого числа) равна второму числу. Например, 220 и 284, 1184 и 1210, 2620 и 2924, 5020 и 5564.
- Вводится целое положительное число. Найти число, которое равно сумме утроенных цифр исходного числа.
- Вводятся два целых положительных числа. Найти сумму их цифр.
3.6.8 Вложенные циклы
Разработать программу на языке С++ для следующих заданий:
- Дано натуральное число
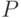 . Вывести все простые числа не превосходящие
. Вывести все простые числа не превосходящие
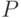 .
. - Дано натуральное число
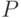 . Вывести все совершённые числа не превосходящие
. Вывести все совершённые числа не превосходящие 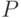 .
. - Вводится последовательность положительных целых чисел, 0 — конец последовательности. Определить количество совершённых чисел в последовательности.
- Вводится последовательность положительных целых чисел, 0 — конец последовательности. Определить количество простых чисел в последовательности.
- Вводится последовательность из
 положительных целых чисел. Для каждого элемента последовательности вычислить факториал.
положительных целых чисел. Для каждого элемента последовательности вычислить факториал. - Вводится последовательность из
 положительных целых чисел. Вывести на экран все числа — палиндромы. Если таких чисел нет, выдать соответствующее сообщение.
положительных целых чисел. Вывести на экран все числа — палиндромы. Если таких чисел нет, выдать соответствующее сообщение. - Вводится последовательность из
 положительных целых чисел. Определить разрядность каждого числа.
положительных целых чисел. Определить разрядность каждого числа. - Вводится последовательность из
 положительных целых чисел. Вывести на экран количество делителей каждого числа.
положительных целых чисел. Вывести на экран количество делителей каждого числа. - Вводится последовательность положительных целых чисел, 0 — конец последовательности. Определить сумму цифр каждого элемента последовательности.
- Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Для каждого набора вывести количество его элементов. Вычислить общее количество элементов.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Для каждого набора вывести количество его элементов. Вычислить общее количество элементов. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Для каждого набора вычислить среднее арифметическое его элементов.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Для каждого набора вычислить среднее арифметическое его элементов. - Даны
 наборов целых чисел по
наборов целых чисел по  элементов в каждом наборе. Для каждого набора найти наибольшее значение его элементов.
элементов в каждом наборе. Для каждого набора найти наибольшее значение его элементов. - Даны
 наборов целых чисел по
наборов целых чисел по  элементов в каждом наборе. Определить, есть ли среди наборов данных знакочередующиеся последовательности.
элементов в каждом наборе. Определить, есть ли среди наборов данных знакочередующиеся последовательности. - Даны
 наборов целых чисел по
наборов целых чисел по  элементов в каждом наборе. Определить, есть ли среди наборов данных строго возрастающие последовательности.
элементов в каждом наборе. Определить, есть ли среди наборов данных строго возрастающие последовательности. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Для каждого набора найти наименьшее значение его элементов.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Для каждого набора найти наименьшее значение его элементов. - Даны
 наборов целых чисел по
наборов целых чисел по  элементов в каждом наборе. Для каждого набора вычислить произведение ненулевых элементов.
элементов в каждом наборе. Для каждого набора вычислить произведение ненулевых элементов. - Даны
 наборов целых чисел по
наборов целых чисел по  элементов в каждом наборе. Найти наибольшее число для всех наборов.
элементов в каждом наборе. Найти наибольшее число для всех наборов. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Вычислить среднее арифметическое всех элементов во всех наборах.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Вычислить среднее арифметическое всех элементов во всех наборах. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество возрастающих наборов.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество возрастающих наборов. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество убывающих наборов.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество убывающих наборов. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество наборов не являющихся знакочередующимися.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество наборов не являющихся знакочередующимися. - Дано
 наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество наборов элементы которых не возрастают и не убывают.
наборов ненулевых целых чисел. Признаком завершения каждого набора является число 0. Найти количество наборов элементы которых не возрастают и не убывают. - Даны целые положительные числа
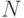 и
и 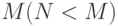 . Вывести все целые числа от
. Вывести все целые числа от  до
до  включительно; при этом каждое число должно выводиться столько раз, каково его значение (например, число 5 выводится 5 раз).
включительно; при этом каждое число должно выводиться столько раз, каково его значение (например, число 5 выводится 5 раз). - Дано целое число
 . Найти сумму
. Найти сумму 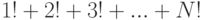
- Даны целые числа
 и
и 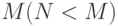 . Вывести все целые числа от
. Вывести все целые числа от  до
до  включительно; при этом число
включительно; при этом число  должно выводиться 1 раз, число
должно выводиться 1 раз, число 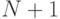 должно выводиться 2 раза и т. д.
должно выводиться 2 раза и т. д.
