НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 11: Компьютерное моделирование при обработке опытных данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 6169 / 2301 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Необходимым условием существования минимума функции S является равенство нулю ее частных производных по каждой a_j.

$\left\{ \begin{array}{l} \frac{\delta s}{\delta a_0} \to 2\sum \limits_{i=0}^{n}((a_0 x_i^0 + a_1 x_i^1 + \ldots + a_m x_i^m - y_i)x_i^0) = 0\\ \frac{\delta s}{\delta a_1} \to 2\sum \limits_{i=0}^{n}((a_0 x_i^0 + a_1 x_i^1 + \ldots + a_m x_i^m - y_i)x_i^1) = 0\\ \frac{\delta s}{\delta a_2} \to 2\sum \limits_{i=0}^{n}((a_0 x_i^0 + a_1 x_i^1 + \ldots + a_m x_i^m - y_i)x_i^2) = 0\\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots\\ \frac{\delta s}{\delta a_m} \to 2\sum \limits_{i=0}^{n}((a_0 x_i^0 + a_1 x_i^1 + \ldots + a_m x_i^m - y_i)x_i^m) = 0 \end{array} \right.$

В результате получили систему линейных уравнений. Раскрывая скобки и перенося свободные члены в правой части уравнений, получим в нормальной форме систему линейных уравнений:

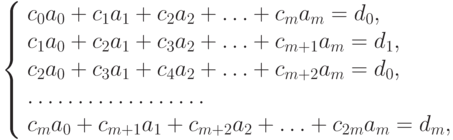$\left\{ \begin{array}{l} c_0 a_0 + c_1 a_1 + c_2 a_2 + \ldots + c_m a_m =d_0,\\ c_1 a_0 + c_2 a_1 + c_3 a_2 + \ldots + c_{m+1} a_m =d_1,\\ c_2 a_0 + c_3 a_1 + c_4 a_2 + \ldots + c_{m+2} a_m =d_0,\\ \ldots \ldots \ldots \ldots \ldots \ldots\\ c_m a_0 + c_{m+1} a_1 + c_{m+2} a_2 + \ldots + c_{2m} a_m =d_m, \end{array} \right.$

( 11.12)

где

a_j - неизвестные системы линейных уравнений (11.12),

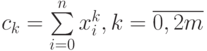$c_k = \sum \limits_{i=0}^{n} x_i^k, k=\overline{0,2m}$ - коэффициенты системы линейных уравнений (11.12),

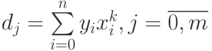$d_j = \sum \limits_{i=0}^{n} y_i x_i^k, j=\overline{0,m}$ - свободные члены системы линейных уравнений (11.12),

Порядок системы равен m+1.

При ручном счете коэффициенты c_k и свободные члены d_j удобно определять, пользуясь таблицей 11.2:

Таблица 11.2.
i	x_i⁰	x_i¹	x_i²	...	x_i^2m	x_i⁰ y_i	x_i¹ y_i	...	x_i^m
0	1
1	1
2	1
...	...
N	1
$\sum_{i=o}^n$	c₀	c₁	c₂	...	c_2m	d₀	d₁	...	d_m

Программирование метода наименьших квадратов (МНК)

Изменим индексацию в системе (11.12). В результате получим:

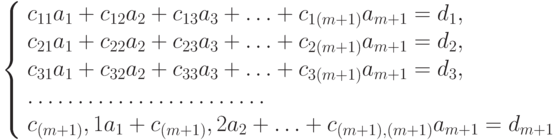$\left\{ \begin{array}{l} c_{11}a_1 + c_{12}a_2 + c_{13}a_3 + \ldots + c_{1(m+1)} a_{m+1} = d_1,\\ c_{21}a_1 + c_{22}a_2 + c_{23}a_3 + \ldots + c_{2(m+1)} a_{m+1} = d_2,\\ c_{31}a_1 + c_{32}a_2 + c_{33}a_3 + \ldots + c_{3(m+1)} a_{m+1} = d_3,\\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots\\ c_{(m+1)},1a_1 + c_{(m+1)},2a_2 + \ldots + c_{(m+1),(m+1)} a_{m+1} = d_{m+1} \end{array} \right.$

( 11.13)

где

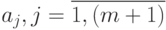$a_j, j=\overline{1,(m+1)}$ - неизвестные системы линейных уравнений (11.13),

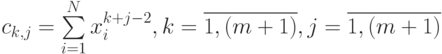$c_{k,j} = \sum \limits_{i=1}^{N} x_i^{k+j-2}, k = \overline{1,(m+1)}, j = \overline{1,(m+1)}$ - коэффициенты системы линейных уравнений (11.13),

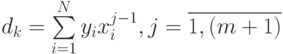$d_k = \sum \limits_{i=1}^{N} y_i x_i^{j-1}, j = \overline{1,(m+1)}$ - свободные члены системы линейных уравнений (11.13),

(x_i, y_i) - координаты узловых точек табличной функции, 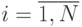$i=\overline{1,N}$ ,

N - количество узловых точек,

m - степень аппроксимирующего многочлена вида:

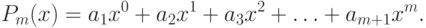$P_m(x) = a_1 x^0 + a_2 x^1 + a_3 x^2 + \ldots + a_{m+1} x^m.$

( 11.14)

Алгоритм задачи:

Строим систему линейных уравнений (11.13). Определяем коэффициенты c_k,j и свободные члены d_k. Т.к. система (11.13) симметрична относительно главной диагонали, то достаточно определить только наддиагональные элементы системы.
Решаем систему (11.13) методом Гаусса. Находим коэффициенты aj многочлена (11.14).
Строим аппроксимирующий многочлен (11.14) и определяем его значение в каждой узловой точке P_i = P_m(x_i).
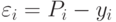Находим уклонение каждой узловой точки $\varepsilon_i = P_i - y_i$ .
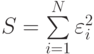Находим сумму квадратов уклонений по всем узловым точкам $S = \sum \limits_{i=1}^{N} \varepsilon_i^2$ .
Находим остаточную дисперсию $D=\frac{S}{N-(m+1)}$ .

Для построения аппроксимирующего многочлена (11.11) и вычисления его значения в каждой узловой точке используем рациональную форму многочлена:

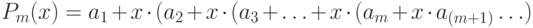$P_m(x) = a_1 + x \cdot (a_2 + x \cdot (a_3 + \ldots + x \cdot (a_m + x \cdot a_{(m+1)} \ldots)$

( 11.15)

Тогда для вычисления значения многочлена (11.15) удобно пользоваться схемой Горнера. Рекуррентная формула по схеме Горнера имеет вид:

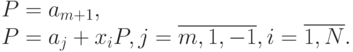
$P = a_{m+1},\\ P = a_j + x_i P, j=\overline{m,1,-1}, i=\overline{1,N}.$

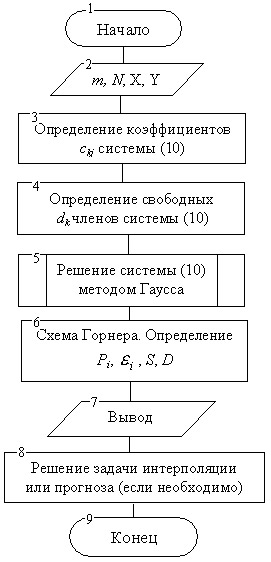
Укрупненная схема алгоритма МНК представлена на рис.11.7. Схемы алгоритмов основных блоков представлены на рисунках 11.8-11.10.

Рис. 11.7. Укрупненная схема алгоритма аппроксимации методом наименьших квадратов

Дальше >>

Авторизоваться

Введение в математическое моделирование

Компьютерное моделирование при обработке опытных данных

Программирование метода наименьших квадратов (МНК)

Алгоритм задачи:

Вопросы и ответы