Игры. Клеточные автоматы
Теорема Бутона
Пусть 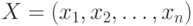 - позиция в игре Ним с n кучками. Ним-суммой позиции X называется число
- позиция в игре Ним с n кучками. Ним-суммой позиции X называется число 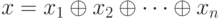 .
.
Теорема (Бутона). Позиция  является проигрышной в игре "Ним" тогда и только тогда, когда ее ним-сумма равна нулю.
является проигрышной в игре "Ним" тогда и только тогда, когда ее ним-сумма равна нулю.
Доказательство. Пусть  - ненулевая позиция с нулевой ним-суммой, т. е.
- ненулевая позиция с нулевой ним-суммой, т. е. 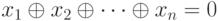 . Будем считать, что
. Будем считать, что 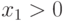 .
.
Возьмем из кучки  произвольное ненулевое число камней k, так что
произвольное ненулевое число камней k, так что 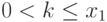 . Заметим, что
. Заметим, что 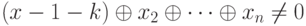 . В самом деле, если
. В самом деле, если  , то из свойства 2 утверждения 2 следует, что
, то из свойства 2 утверждения 2 следует, что 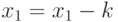 , что невозможно, так как k > 0. Аналогично для остальных кучек. Таким образом, произвольный ход из позиции с нулевой ним-суммой приводит к позиции с ненулевой ним-суммой.
, что невозможно, так как k > 0. Аналогично для остальных кучек. Таким образом, произвольный ход из позиции с нулевой ним-суммой приводит к позиции с ненулевой ним-суммой.
Покажем теперь, что из позиции с ненулевой ним-суммой существует хотя бы один ход в позицию с нулевой ним-суммой.
Пусть 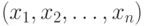 - позиция с ненулевой ним-суммой. Положим
- позиция с ненулевой ним-суммой. Положим 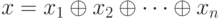 . Пусть двоичное представление числа x содержит i разрядов. Возьмем кучку j, такую, что в двоичном представлении числа
. Пусть двоичное представление числа x содержит i разрядов. Возьмем кучку j, такую, что в двоичном представлении числа 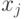 в i-м разряде стоит 1.
в i-м разряде стоит 1.
Покажем, что  . В самом деле, в i-м разряде двоичного представления числа
. В самом деле, в i-м разряде двоичного представления числа 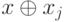 стоит 0, а значения, стоящие в старших разрядах, совпадают со значениями числа
стоит 0, а значения, стоящие в старших разрядах, совпадают со значениями числа 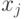 , стоящими в тех же разрядах.
, стоящими в тех же разрядах.
Далее, заменим в выражении  элемент
элемент 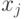 на элемент
на элемент 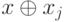 . В результате получим:
. В результате получим:

Таким образом, если из кучки j забрать 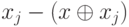 камней, то получится позиция с нулевой ним-суммой.
камней, то получится позиция с нулевой ним-суммой.
Следовательно, позиции с нулевой ним-суммой являются проигрышными, а остальные позиции - выигрышными. Выигрышная стратегия - ходить так, чтобы привести противника в позицию с нулевой ним-суммой, что всегда возможно сделать из позиции с ненулевой ним-суммой.
Пример 2. Для игры "Ним" с тремя кучками, содержащими 3, 5 и 7 камней, имеем: 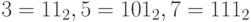 .
.
Найдем ним-сумму начальной позиции.
В нулевом разряде каждого числа стоит 1. Поэтому следует либо оставить  , или 2 камня в первой кучке, либо
, или 2 камня в первой кучке, либо  , или 4 камня во второй, либо
, или 4 камня во второй, либо  , или 6 камней в третьей кучке.
, или 6 камней в третьей кучке.
Пример 3. Рассмотрим игру "Ним" с 4 кучками, которые содержат 17, 24, 7 и 11 камней. Имеем: 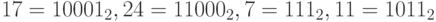 .
.
Найдем ним-сумму x начальной позиции:
Таким образом, 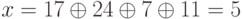 . Старший ненулевой разряд ним-суммы отличен от 0 только у числа 7. По теореме Бутона, в третьей кучке должно остаться
. Старший ненулевой разряд ним-суммы отличен от 0 только у числа 7. По теореме Бутона, в третьей кучке должно остаться  , или 2 камня. Соответственно, взять из нее следует 5 камней. В результате противнику достанется проигрышная позиция с 4 кучками, содержащими 17, 24, 2 и 11 камней.
, или 2 камня. Соответственно, взять из нее следует 5 камней. В результате противнику достанется проигрышная позиция с 4 кучками, содержащими 17, 24, 2 и 11 камней.
Функция Шпрага-Гранди. Сумма игр
Рассмотрим функцию Шпрага-Гранди. Областью определения этой функции является множество позиций игры, а областью значений - множество неотрицательных целых чисел.
Функция Шпрага-Гранди определяется индуктивно. Если из позиции нельзя сделать ход, то значение функции в ней полагается равным 0. В противном случае значение функции в позиции S полагается равным наименьшему неотрицательному числу, которое отсутствует среди значений функции в позициях, в которые можно за один ход попасть из S.
Утверждение 3. Позиция является проигрышной тогда и только тогда, когда значение функции Шпрага-Гранди в этой позиции равно 0.
Доказательство. Пусть значение функции Шпрага-Гранди в позиции S равно 0. Тогда либо из позиции S нельзя сделать ход, либо все ходы из нее приводят к таким позициям, для которых значение функции Шпрага-Гранди положительно. Обратно, пусть значение функции Шпрага-Гранди в позиции S положительно. Тогда среди позиций, в которые можно из нее перейти, существует позиция, значение функции Шпрага-Гранди которой равно нулю.
Рассмотрим игру "Ним" с одной кучкой. Пусть P - множество позиций игры и  - множество неотрицательных целых чисел. Обозначим через
- множество неотрицательных целых чисел. Обозначим через 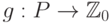 функцию Шпрага-Гранди.
функцию Шпрага-Гранди.
Утверждение 4. Функция Шпрага-Гранди на множестве позиций игры "Ним" с одной кучкой имеет вид: g(m) = m.
Доказательство. В позиции (m) существует m ходов: из кучки можно взять от 1 до m камней. Используем индукцию по m.
При m = 0 утверждение верно. Предположим, что утверждение верно для всех кучек, содержащих не более k камней. Пусть кучка содержит k + 1 камень. Из этой кучки можно взять от 1 до k + 1 камней и перейти при этом в позиции 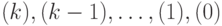 . По предположению индукции, значение функции Шпрага-Гранди в этих позициях соответственно равно
. По предположению индукции, значение функции Шпрага-Гранди в этих позициях соответственно равно 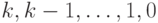 . Наименьшее целое неотрицательное число, которое не входит во множество полученных значений, равно k + 1. Следовательно, g(k + 1) = k + 1.
. Наименьшее целое неотрицательное число, которое не входит во множество полученных значений, равно k + 1. Следовательно, g(k + 1) = k + 1.
Для доказательства теоремы Шпрага-Гранди понадобится еще одно свойство операции  .
.
Утверждение 5. Если  , то
, то 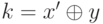 для некоторого x', такого что x' < x, или
для некоторого x', такого что x' < x, или 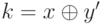 для некоторого
для некоторого 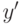 , такого что
, такого что 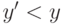 .
.
Доказательство. Пусть i - самый старший разряд двоичного представления, в котором число  отличается от k. В этом разряде у числа k стоит 0, а у числа
отличается от k. В этом разряде у числа k стоит 0, а у числа  . Поэтому в i-ом разряде одного из чисел x и y стоит 1, а другого - 0. Пусть в i-ом разряде числа x стоит 0
. Поэтому в i-ом разряде одного из чисел x и y стоит 1, а другого - 0. Пусть в i-ом разряде числа x стоит 0
Покажем, что  . Действительно, пусть разряд j старше разряда i. Тогда значения j-го разряда чисел
. Действительно, пусть разряд j старше разряда i. Тогда значения j-го разряда чисел  и k совпадают. Поэтому в j-ом разряде числа
и k совпадают. Поэтому в j-ом разряде числа  стоит то же значение, что и в j-ом разряде числа
стоит то же значение, что и в j-ом разряде числа 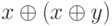 , равного y. Следовательно, i - это самый старший разряд двоичного представления числа
, равного y. Следовательно, i - это самый старший разряд двоичного представления числа  , в котором оно отличается от y. Но в i-м разряде числа
, в котором оно отличается от y. Но в i-м разряде числа  стоит 0, а в том же разряде числа y стоит 1. Таким образом,
стоит 0, а в том же разряде числа y стоит 1. Таким образом,  . Положим
. Положим 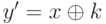 . Имеем:
. Имеем:
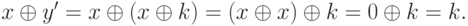
Пусть P - множество позиций игры G, а F - бинарное отношение на P, такое что F = {(p, q) | существует ход, который переводит p в q}.
Пусть  и
и 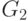 - игры,
- игры, 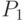 и
и 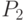 - множества позиций игр
- множества позиций игр  и
и 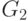 , а
, а 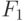 и
и  - определенные выше бинарные отношения на множествах
- определенные выше бинарные отношения на множествах 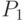 и
и 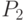 , соответственно
, соответственно
Суммой игр  и
и 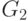 называется игра G с множеством позиций P, таким что
называется игра G с множеством позиций P, таким что 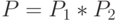 , а отношение F на множестве P имеет вид:
, а отношение F на множестве P имеет вид:
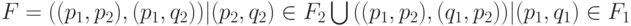
Пример 4. Игра "Ним" с двумя кучками является суммой двух игр "Ним" с одной кучкой.
Обозначим через 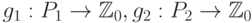 и
и  функции Шпрага-Гранди игр
функции Шпрага-Гранди игр 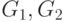 и
и 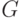 , соответственно.
, соответственно.
Теорема (Шпрага-Гранди). Для любой позиции  игры
игры 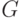 является верным следующее равенство:
является верным следующее равенство:

Доказательство. Используем индукцию по максимальному числу оставшихся ходов.
Из позиции  игры G нельзя сделать ход тогда и только тогда, когда его нельзя сделать ни из позиции
игры G нельзя сделать ход тогда и только тогда, когда его нельзя сделать ни из позиции 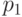 в игре
в игре 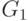 , ни из позиции
, ни из позиции  в игре
в игре  . Поэтому
. Поэтому 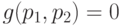 , тогда и только тогда, когда
, тогда и только тогда, когда 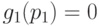 и
и 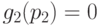 , а, следовательно,
, а, следовательно, 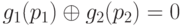 .
.
Пусть  - позиция, в которую существует ход из позиции
- позиция, в которую существует ход из позиции  . Тогда, по определению, либо
. Тогда, по определению, либо 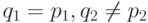 , либо
, либо 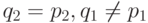 .
.
Покажем, что 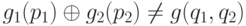 . От противного. Предположим, что
. От противного. Предположим, что 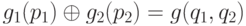 . Пусть
. Пусть  . Тогда, по предположению индукции,
. Тогда, по предположению индукции,  . Следовательно, выполняется условие
. Следовательно, выполняется условие  , из которого по свойству 2 утверждения 2 следует, что
, из которого по свойству 2 утверждения 2 следует, что  . Но в позицию
. Но в позицию 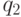 существует ход из позиции
существует ход из позиции 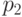 в игре
в игре 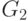 , поэтому данное равенство невозможно по определению функции Шпрага-Гранди. Случай
, поэтому данное равенство невозможно по определению функции Шпрага-Гранди. Случай  рассматривается аналогично.
рассматривается аналогично.
Итак, число  не совпадает ни с одним из значений функции Шпрага-Гранди в позициях, которые получаются с помощью некоторого хода из позиции
не совпадает ни с одним из значений функции Шпрага-Гранди в позициях, которые получаются с помощью некоторого хода из позиции  .
.
Покажем, что число  является наименьшим целым неотрицательным числом, которое не принадлежит множеству
является наименьшим целым неотрицательным числом, которое не принадлежит множеству  .
.
Пусть 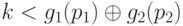 , где
, где  . Из утверждения 5 следует, что либо
. Из утверждения 5 следует, что либо  для некоторого числа
для некоторого числа 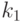 из
из  , такого что
, такого что 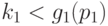 , либо
, либо 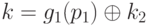 для некоторого
для некоторого 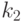 из
из  , такого что
, такого что  .
.
Пусть  . Поскольку
. Поскольку 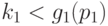 , то, по определению функции Шпрага-Гранди, в игре
, то, по определению функции Шпрага-Гранди, в игре  найдется позиция
найдется позиция 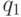 , в которую существует ход из позиции
, в которую существует ход из позиции 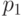 , такая, что
, такая, что  . Следовательно, выполняется соотношение
. Следовательно, выполняется соотношение 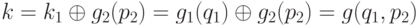 .
.
Последнее равенство верно по предположению индукции.
Заметим, что 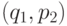 - это позиция, в которую существует ход из позиции
- это позиция, в которую существует ход из позиции  . Таким образом, среди значений функции Шпрага-Гранди в позициях, в которые существует ход из позиции
. Таким образом, среди значений функции Шпрага-Гранди в позициях, в которые существует ход из позиции  , найдется любое неотрицательное целое число, меньшее, чем
, найдется любое неотрицательное целое число, меньшее, чем  . Поэтому
. Поэтому

Следствие. Функция Шпрага-Гранди игры "Ним" с n кучками имеет вид:
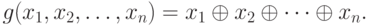
В самом деле, игра "Ним" с n кучками является суммой n игр с одной кучкой. Пусть 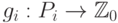 - функция Шпрага-Гранди i-ой игры, определенная на множестве ее позиций
- функция Шпрага-Гранди i-ой игры, определенная на множестве ее позиций 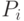 , для
, для 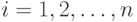 . Из утверждения 3 следует, что
. Из утверждения 3 следует, что 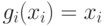 . По методу математической индукции получаем указанную выше формулу.
. По методу математической индукции получаем указанную выше формулу.
Таким образом, теорема Бутона является следствием теоремы Шпрага-Гранди.
Пример 5. Рассмотрим следующую игру. В кучке имеется 9 камней. Два игрока ходят по очереди. За один ход игрок может взять от 1 до 3 камней. Выигрывает тот, кто берет последний камень. Построим функцию Шпрага-Гранди.
Пусть позицией является число камней в кучке. Тогда множество позиций игры описывается целыми числами от 0 до 9. Последовательно находим:
g(0) = 0; g(1) = 1; g(2) = 2; g(3) = 3; g(4) = 0; g(5) = 1; g(6) = 2; g(7) = 3; g(8) = 0; g(9) = 1.
Покажем, что в общем случае, g(m) = m mod 4, для 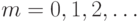 В самом деле, значение функции Шпрага-Гранди в позиции m определяется значениями этой функции в позициях m - 1, m - 2 и m - 3, для
В самом деле, значение функции Шпрага-Гранди в позиции m определяется значениями этой функции в позициях m - 1, m - 2 и m - 3, для  . Применим индукцию по m. При
. Применим индукцию по m. При  утверждение верно. Предположим, что оно верно при m = k, где
утверждение верно. Предположим, что оно верно при m = k, где 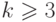 . Пусть m = k + 1. По предположению индукции, в позициях k, k - 1 и k - 2 значение функции Шпрага-Гранди равно трем последовательным остаткам от деления на 4. Поэтому значение функции Шпрага-Гранди в позиции k + 1 равно недостающему остатку от деления на 4, так что g(m) = m mod 4 при
. Пусть m = k + 1. По предположению индукции, в позициях k, k - 1 и k - 2 значение функции Шпрага-Гранди равно трем последовательным остаткам от деления на 4. Поэтому значение функции Шпрага-Гранди в позиции k + 1 равно недостающему остатку от деления на 4, так что g(m) = m mod 4 при  .
.
Таким образом, проигрышными являются позиции, кратные 4. В частности, позиция 9 является выигрышной. Выигрышная стратегия игры - оставлять другому игроку число камней, кратное 4.


