НОУ ИНТУИТ | Введение в теорию автоматов. Лекция 5: Синтез структурного автомата

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Вятский государственный университет

Опубликован: 24.04.2008 | Доступ: свободный | Студентов: 2132 / 435 | Оценка: 3.44 / 3.17 | Длительность: 06:01:00

Теги: d-триггер, RS, абстрактный автомат, автомат, автомат мили, автомат мура, автоматы, алгоритмы, граф, дуга, история, ЛСА, микропрограмма, проектирование, теория, топология, электронная почта, элементы

|

Вам нравится? Нравится 30 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

5.4.Этапы синтеза

Находим количество элементов памяти , ( - число состояний абстрактного автомата) и кодируем состояния абстрактного автомата (табл.5.1).

Таблица 5.1.
a_m\ $\tau_1 \tau_2 \dots \tau_R$ $\tau_1 \tau_2 \dots \tau_R$

a₁

a₂

…

a_M
Кодируем входные и выходные сигналы, то есть
- находим количество входов структурного автомата , ( - число входных сигналов абстрактного автомата);
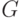- количество выходов 1 типа ; ( - число выходных сигналов 1 типа);
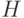- количество выходов 2 типа , ( - число выходных сигналов 2 типа) и кодируем входные (табл.5.2) и выходные сигналы (табл.5.3) и (табл.5.4) абстрактного автомата.
  
  Таблица 5.2.
  z _f / x₁ x_L x₁x₂…x₁
  
  z
  
  z
  
  …
  
  z
  
  Таблица 5.3.
  w_f/y₁y₂…y_N y₁y₂…y_N
  
  w₁
  
  w₂
  
  …
  
  w_G
  
  Таблица 5.4.
  u_h/r₁ r₂…r_D r₁ r₂…r_D
  
  u₁
  
  u₂
  
  …
  
  u_H
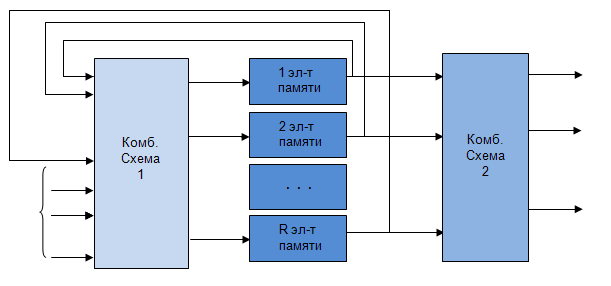
Структурный автомат представляем обобщенной схемой (рис.5.6).

Рис. 5.6.
Составляем закодированную таблицу выходов автомата и по ней записываем уравнения выходов.
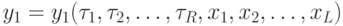- $y_1= y_1(\tau_1, \tau_2, \dots, \tau_R, x_1, x_2, \dots, x_L)$ ;
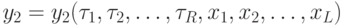- $y_2= y_2(\tau_1, \tau_2, \dots, \tau_R, x_1, x_2, \dots, x_L)$ ;
- . . .
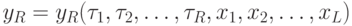- $y_R= y_R(\tau_1, \tau_2, \dots, \tau_R, x_1, x_2, \dots, x_L)$ ;
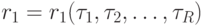- $r_1= r_1(\tau_1, \tau_2, \dots, \tau_R)$ ;
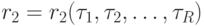- $r_2= r_2(\tau_1, \tau_2, \dots, \tau_R)$ ;
- . . .
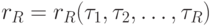- $r_R= r_R(\tau_1, \tau_2, \dots, \tau_R)$ ;
- . . .
Составляем закодированную таблицу переходов автомата и по ней записываем уравнения для функций возбуждения, используя таблицы переходов соответсвующих элементов памяти.
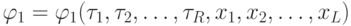- $\varphi_1= \varphi_1(\tau_1, \tau_2, \dots, \tau_R, x_1, x_2, \dots, x_L)$ ;
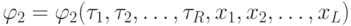- $\varphi_2= \varphi_2(\tau_1, \tau_2, \dots, \tau_R, x_1, x_2, \dots, x_L)$ ;
- . . .
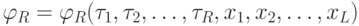- $\varphi_R= \varphi_R(\tau_1, \tau_2, \dots, \tau_R, x_1, x_2, \dots, x_L)$ ;
Уравнения функций возбуждения и выходов минимизируются (по картам Карно, например) и по ним строится схема в заданном функционально - логическом базисе ({И, ИЛИ, НЕ}, {И-НЕ}, {ИЛИ-НЕ}).