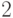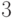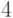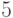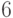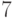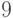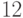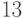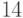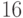|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Введем необходимые обозначения. Пусть  — непустое слово
в некотором алфавите, а
— непустое слово
в некотором алфавите, а 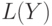 — наибольший собственный префикс
слова
— наибольший собственный префикс
слова  ,
являющийся его суффиксом. Тогда справедливы следующие утверждения:
,
являющийся его суффиксом. Тогда справедливы следующие утверждения:
- Слова
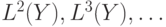 являются собственными
префиксами и суффиксами слова
являются собственными
префиксами и суффиксами слова  .
. - Последовательность
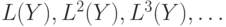 обрывается на пустом слове.
обрывается на пустом слове. - Любой префикс слова
 , являющийся его суффиксом, находится
в последовательности
, являющийся его суффиксом, находится
в последовательности 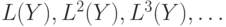
Пример.
Пусть 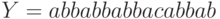 . Тогда
. Тогда
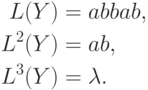
Определение.
Функцией откатов для слова  называют
функцию
называют
функцию  ,
определяемую соотношением
,
определяемую соотношением 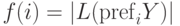 , где
, где  — префикс длины
— префикс длины  слова
слова  .
.
В нашем примере функция 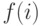 задается следующей таблицей:
задается следующей таблицей:
Алгоритм
Кнута-Морриса-Пратта построения функции откатов для слова  :
:
![\formula{
f(1) := 0;\\
\t for\ i :=1\ \t to\ n - 1\ \t do\\
\mbox{}\q \t begin\ j := f(i);\\
\mbox{}\q\q \t while\ (Y[j + 1] \ne
Y[i + 1]) \& (j > 0)\
\t do\ j := f[j];\\
\mbox{}\q\q \t if\ Y[j + 1] = Y[i + 1]\
\t then\ f[i + 1] := j + 1\
\t else\ f[i +1] := 0;\\
\mbox{}\q\t end
}](/sites/default/files/tex_cache/7596c395fc93452c16152aae67965f73.png)
Для разъяснения работы алгоритма рассмотрим ситуацию, возникшую при
обработке слова  на шаге
на шаге 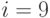 . К этому моменту
вычислены значения
. К этому моменту
вычислены значения 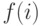 при
при  :
:
Выполняем ![j:= f[i]](/sites/default/files/tex_cache/2028f7b6fffbf647331ad41c928204e9.png)
![(f[i] = 6)](/sites/default/files/tex_cache/8c360c25347ecace006038505af6785b.png) . Видим, что
условие во внутреннем цикле не выполняется из-за первого сомножителя, так
как
. Видим, что
условие во внутреннем цикле не выполняется из-за первого сомножителя, так
как ![Y[i + 1] = Y [j + 1]](/sites/default/files/tex_cache/af1f85609e7593062132fc5614517935.png) , поэтому тело
внутреннего цикла не выполняется, и далее в соответствии с алгоритмом
вычисляем
, поэтому тело
внутреннего цикла не выполняется, и далее в соответствии с алгоритмом
вычисляем ![f[i + 1] := j + 1 (j + 1 = 7)](/sites/default/files/tex_cache/6c38988a0b1244f09ebb4ffc2bc54e1c.png) и
и 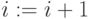 .
.
Пришли к следующей ситуации 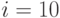 :
:
Вычисляем ![j:= f [i]](/sites/default/files/tex_cache/981f370157ac1313794775498ed52363.png)
![(f[i] = 7)](/sites/default/files/tex_cache/b838cd6fd1d72765d76327715e3a2fab.png) . Видим, что
условие
. Видим, что
условие ![(Y[i + 1] \ne Y[j + 1] \& j > 0](/sites/default/files/tex_cache/d8b1be2b5d52c8f44e9c5af2d88d7410.png) )
во внутреннем цикле выполняется. Следовательно,
вычисляется новое значение
)
во внутреннем цикле выполняется. Следовательно,
вычисляется новое значение ![j := f[j] (= 4)](/sites/default/files/tex_cache/03142bc1014e057d8bee1effa1a90f79.png) ; условие
опять выполнено, вычисляем новое
; условие
опять выполнено, вычисляем новое ![j := f[j] = 1](/sites/default/files/tex_cache/c3e482a0031a2b19521b91d06e005145.png) и на
этот раз условие выполняется, снова вычисляем
и на
этот раз условие выполняется, снова вычисляем ![j := f[j] (= 0)](/sites/default/files/tex_cache/0bfbacc3fd9588c77686d662c6b52c53.png) .
Наконец внутренний цикл завершается, причиной завершения является
невыполнение условия
.
Наконец внутренний цикл завершается, причиной завершения является
невыполнение условия  и поэтому
и поэтому ![f[i + 1] :=
0](/sites/default/files/tex_cache/2eb5492c0a672115c005e843d664e300.png) . Итак, вычислено
. Итак, вычислено ![f[11] = 0](/sites/default/files/tex_cache/3c5dfef49b889b3bf13b58f7f51b2a0c.png) .
.
Оценим трудоемкость алгоритма.
Обработка очередной буквы ![Y[i + 1]](/sites/default/files/tex_cache/251b3072d2be7d35b6bdb986e8912c68.png) может потребовать многих
итераций во внутреннем цикле. Обозначим их число через
может потребовать многих
итераций во внутреннем цикле. Обозначим их число через 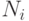 .
Заметим, что каждая итерация внутреннего цикла уменьшает
.
Заметим, что каждая итерация внутреннего цикла уменьшает 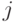 по
крайней мере на
по
крайней мере на  . С другой стороны, переход к следующему
значению
. С другой стороны, переход к следующему
значению  увеличивает
увеличивает 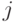 не более чем на
не более чем на  . Таким образом,
имеем неравенства
. Таким образом,
имеем неравенства
![\eq*{
f[i + 1] \le f[i] - N_i + 1
}](/sites/default/files/tex_cache/89aff233374aea6a54b5c8270731409a.png)
или
![\eq*{
N_i \le f[i] - f[i + 1] + 1.
}](/sites/default/files/tex_cache/caca25107fdb0074ca515d8eb0b2a569.png)
Суммируя последнее неравенство по  от
от  до
до 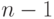 , получим
, получим
![\eq*{
\suml_{i=1}^{n-1}N_{i} = f[1]-f[n] + n - 1\le n.\vspace{-1mm}
}](/sites/default/files/tex_cache/a11de2f7ddb6a6836fd71c787035e203.png)
 .
.Построение детерминированного конечного
автомата по функции откатов. Задача заключается
в том, чтобы построить конечный автомат,
который, читая произвольный текст, приходил бы в финальное состояние,
обнаружив фрагмент, совпадающий с заданным словом  .
.
Изложенный ниже алгоритм строит переходную функцию 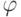 автомата
автомата
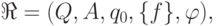
 ,
,  ,
,  .
Предполагаем, что функция откатов
.
Предполагаем, что функция откатов  уже построена.
уже построена.![\formula{
\t for\ j := 1\ \t to\ n\ \t do\
\varphi[j - 1, Y_j]:=j;\\
\t for\ a \in A,\ a \ne Y_1\
\t do\ \varphi[0, a]:= 0;\\
\t for\ j :=1\ \t to\ n\ \t do
for\ a \in A,\
a \ne Y_{j+1}\ \t do\ \varphi[j, a] :=
\varphi [f[j], a];
}](/sites/default/files/tex_cache/17f6b649fb76a32cca767d274960a5a6.png)
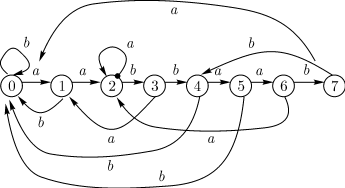
Для слова  получим автомат, заданный диаграммой,
изображенной на рис. 13.4.
получим автомат, заданный диаграммой,
изображенной на рис. 13.4.