Управляющие конструкции языка Си. Представление программ в виде функций. Работа с памятью. Структуры
Пример: решение квадратного уравнения
Рассмотрим простой пример, в котором применяется конструкция "если...иначе": требуется решить квадратное уравнение
ax2+bx+c = 0
Программа должна ввести с клавиатуры терминала числа a, b, c и затем напечатать ответ. После ввода надо проверить корректность введенных чисел - коэффициент a должен быть отличен от нуля (иначе уравнение перестает быть квадратным, тогда формула решения квадратного уравнения неприменима). В зависимости от знака дискриминанта уравнение может не иметь решений. Программа должна напечатать либо сообщение об отсутствии решений, либо два корня уравнения (возможно, совпадающие в случае нулевого дискриминанта).
Для печати на экран терминала и ввода информации с клавиатуры используются функции ввода-вывода из стандартной библиотеки Си. Отметим, что функции стандартного ввода-вывода не являются частью языка Си: Си не содержит средств ввода-вывода. Однако любой компилятор обычно предоставляет набор библиотек, в который входит стандартный ввод-вывод. Описания функций ввода-вывода содержатся в заголовочном файле stdio.h, который подключается с помощью строки
#include <stdio.h>
Мы используем две функции: функцию printf вывода по формату и функцию scanf ввода по формату. У обеих этих функций число аргументов переменное, первым аргументом всегда является форматная строка. В случае функции printf обычные символы форматной строки просто выводятся на экран терминала. Например, в рассмотренном ранее примере "Hello, World!" текст выводился на экран с помощью строки прoграммы
printf("Hello, World!\n");(Здесь ' \n ' - символ конца строки, т.е. перевода курсора в начало следующей строки.) Единственным аргументом функции printf в данном случае служит форматная строка.
Кроме обычных символов, форматная строка может включать символы формата, которые при выводе заменяются значениями остальных аргументов функции printf, начиная со второго аргумента. Для каждого типа данных Си имеются свои форматы. Формат начинается с символа процента ' % '. После процента идет необязательный числовой аргумент, управляющий представлением данных. Наконец, далее идет одна или несколько букв, задающих тип выводимых на печать данных. Для вывода чисел можно использовать следующие форматы:
%d вывод целого числа типа int (d - от decimal) %lf вывод вещ. числа типа double (lf - от long float)
Например, для печати целого числа n можно использовать строку
printf("n = %d\n", n);Здесь формат " %d " будет заменен на значение переменной n. Пусть, к примеру, n = 15. Тогда при выполнении функции printf будет напечатана строка
n = 15
При печати вещественного числа компьютер сам решает, сколько знаков после десятичной точки следует напечатать. Если нужно повлиять на представление числа, следует использовать необязательную часть формата. Например, формат
%.3lf
применяется для печати значения вещественного числа в форме с тремя цифрами после десятичной точки. Пусть значение вещественной переменной x равно единице. Тогда при выполнении функции
printf("ответ = %.3lf\n", x);будет напечатана строка
ответ = 1.000
При вызове функции форматного ввода scanf форматная строка должна содержать только форматы. Этим функция scanf отличается от printf. Вместо значений печатаемых переменных или выражений, как в функции printf, функция scanf должна содержать указатели на вводимые переменные! Для начинающих это постоянный источник ошибок. Необходимо запомнить: функции scanf нужно передавать адреса переменных, в которые надо записать введенные значения. Если вместо адресов переменных передать их значения, то функция scanf все равно проинтерпретирует полученные значения как адреса, что при выполнении вызовет попытку записи по некорректным адресам памяти и, скорее всего, приведет к ошибке типа Segmentation fault. Пример: пусть нужно ввести значения трех вещественных переменных a, b, c. Тогда следует использовать фрагмент
scanf("%lf%lf%lf", &a, &b, &c);Ошибка, которую часто совершают начинающие: передача функции scanf значений переменных вместо адресов:
scanf("%lf%lf%lf", a, b, c); // Ошибка! Передаются
// значения вместо указателейПомимо стандартной библиотеки ввода-вывода, в Си-программах широко используется стандартная библиотека математических функций. Ее описания содержатся в стандартном заголовочном файле math.h, который подключается строкой
#include <math.h>
Стандартная математическая библиотека содержит математические функции sin, cos, exp, log (натуральный логарифм), fabs (абсолютная величина вещ. числа) и многие другие. Нам необходима функция sqrt, вычисляющая квадратный корень вещественного числа.
Итак, приведем полный текст программы, решающей квадратное уравнение; он содержится в файле " squareEq.cpp ".
#include <stdio.h> // Описания стандартного ввода-вывода
#include <math.h> // Описания математической библиотеки
int main() {
double a, b, c; // Коэффициенты уравнения
double d; // Дискриминант
double x1, x2; // Корни уравнения
printf("Введите коэффициенты a, b, c:\n");
scanf("%lf%lf%lf", &a, &b, &c);
if (a == 0.0) {
printf("Коэффициент a должен быть ненулевым.\n");
return 1; // Возвращаем код некорректного
} // завершения
d = b*b - 4.0*a*c; // Вычисляем дискриминант
if (d < 0.0) {
printf("Решений нет.\n");
}
else {
d = sqrt(d); // Квадр. корень из дискриминанта
x1 = (-b + d) / (2.0 * a); // Первый корень ур-я
x2 = (-b - d) / (2.0 * a); // Второй корень ур-я
// Печатаем ответ
printf(
"Решения уравнения: x1 = %lf, x2 = %lf\n",
x1, x2
);
}
return 0; // Возвращаем код успешного завершения
}Приведем пример выполнения программы:
Введите коэффициенты a, b, c: 1 2 -3 Решения уравнения: x1 = 1.000000, x2 = -3.000000
Здесь первая и третья строчки напечатаны компьютером, вторая строчка напечатана человеком (ввод чисел заканчивается клавишей перевода строки Enter ).
Цикл while
Конструкция цикла "пока" соответствует циклу while в Си:
while (условие)
действие;Цикл while называют циклом с предусловием, поскольку условие проверяется перед выполнением тела цикла.
Цикл while выполняется следующим образом: сначала проверяется условие. Если оно истинно, то выполняется действие. Затем снова проверяется условие ; если оно истинно, то снова повторяется действие, и так до бесконечности. Цикл завершается, когда условие становится ложным. Пример:
int n, p;
. . .
p = 1;
while (2*p <= n)
p *= 2;В результате выполнения этого фрагмента в переменной p будет вычислена максимальная степень двойки, не превосходящая целого положительного числа n.
Если условие ложно с самого начала, то действие не выполняется ни разу. Это очень облегчает программирование и делает программу более надежной, поскольку исключительные ситуации автоматически правильно обрабатываются. Так, приведенный выше фрагмент работает корректно при n = 1 (цикл не выполняется ни разу).
При ошибке программирования цикл может никогда не кончиться. Чтобы избежать этого, следует составлять программу таким образом, чтобы некоторая ограниченная величина, от которой прямо или косвенно зависит условие в заголовке цикла, монотонно убывала или возрастала после каждого выполнения тела цикла. Это обеспечивает завершение цикла. В приведенном выше фрагменте такой величиной является значение p, которое возрастает вдвое после каждого выполнения тела цикла.
Тело цикла может состоять из одного или нескольких операторов. В последнем случае их надо заключить в фигурные скобки. Советуем заключать тело цикла в фигурные скобки даже в том случае, когда оно состоит всего из одного оператора, - это делает текст программы более наглядным и облегчает его возможную модификацию. Например, приведенный выше фрагмент лучше было бы записать так:
int n, p;
. . .
p = 1;
while (2*p <= n) {
p *= 2;
}Сознательное применение цикла "пока" всегда связано с явной формулировкой инварианта цикла, см. раздел 1.5.2.
Рассмотрим построение цикла "пока" на примере программы вычисления квадратного корня методом деления отрезка пополам.
Пример: вычисление квадратного корня методом деления отрезка пополам
Метод вычисления корня функции с помощью деления отрезка пополам в общем случае уже был рассмотрен в разделе 1.5.2. Пусть надо найти квадратный корень из неотрицательного вещественного числа a с заданной точностью 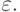 Задача сводится к нахождению корня функции
Задача сводится к нахождению корня функции
y = x2-a
на отрезке [0,b], где b = max(1,a). На этом отрезке функция имеет ровно один корень, поcкольку она монотонно возрастает и на концах отрезка принимает значения разных знаков (или нулевое значение при a = 0 или a = 1 ).
Идея алгоритма состоит в том, что отрезок делится пополам и выбирается та половина, на которой функция принимает значения разных знаков. Эта операция повторяется до тех пор, пока длина отрезка не станет меньше, чем 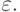 Концы текущего отрезка содержатся в переменных x0, x1. В данном случае функция монотонно возрастает при x >= 0. Инвариантом цикла является утверждение о том, что функция принимает отрицательное или нулевое значение в точке x0 и положительное или нулевое значение в точке x1. Цикл рано или поздно завершается, поскольку после каждого выполнения тела цикла длина отрезка [x0,x1] уменьшается в два раза.
Концы текущего отрезка содержатся в переменных x0, x1. В данном случае функция монотонно возрастает при x >= 0. Инвариантом цикла является утверждение о том, что функция принимает отрицательное или нулевое значение в точке x0 и положительное или нулевое значение в точке x1. Цикл рано или поздно завершается, поскольку после каждого выполнения тела цикла длина отрезка [x0,x1] уменьшается в два раза.
Приведем полный текст программы:
#include <stdio.h> // Описания стандартного ввода-вывода
int main() {
double a; // Число, из которого извлекается корень
double x, x0, x1; // [x0, x1] - текущий отрезок
double y; // Значение ф-ции в точке x
double eps = 0.000001; // Точность вычисления корня
printf("Введите число a:\n");
scanf("%lf", &a);
if (a < 0.0) {
printf("Число должно быть неотрицательным.\n");
return 1; // Возвращаем код
} // некорректного завершения
// Задаем концы отрезка
x0 = 0.0;
x1 = a;
if (a < 1.0) {
x1 = 1.0;
}
// Утверждение: x0 * x0 - a <= 0,
// x1 * x1 - a >= 0
while (x1 - x0 > eps) {
// Инвариант: x0 * x0 - a <= 0,
// x1 * x1 - a >= 0
x = (x0 + x1) / 2.0; // середина отрезка [x0,x1]
y = x * x - a; // значение ф-ции в точке x
if (y >= 0.0) {
x1 = x; // выбираем левую половину отрезка
}
else {
x0 = x; // выбираем правую половину отрезка
}
}
// Утверждение: x0 * x0 - a <= 0,
// x1 * x1 - a >= 0,
// x1 - x0 <= eps
x = (x0 + x1) / 2.0; // Корень := середина отрезка
// Печатаем ответ
printf("Квадратный корень = %lf\n", x);
return 0; // Возвращаем код успешного завершения
}Отметим, что существует более быстрый способ вычисления квадратного корня числа - метод итераций Ньютона, или метод касательных к графику функции, но здесь мы его не рассматриваем.

