|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие числа и операции над ними
Четкие арифметики нечетких треугольных чисел
Вернемся к рассмотрению нечетких треугольных чисел как частного случая
нечетких чисел  -типа, т.е. имеющих вид
-типа, т.е. имеющих вид 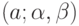 .
.
Мы будем строить арифметику  , где
, где 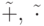 — операции сложения
и умножения, определенные на нечетких треугольных числах. В построенной
арифметике для каждого элемента будут существовать противоположные и обратные
элементы.
Поэтому нет никакой необходимости в определении операций вычитания и
деления.
— операции сложения
и умножения, определенные на нечетких треугольных числах. В построенной
арифметике для каждого элемента будут существовать противоположные и обратные
элементы.
Поэтому нет никакой необходимости в определении операций вычитания и
деления.
Определяя операции сложения и умножения, мы можем вычислять размытость суммы и произведения нечетких треугольных чисел либо по одному алгоритму, либо по разным. Сперва рассмотрим случай, когда размытость суммы и произведения нечетких треугольных чисел вычисляется по одному алгоритму. Определим операции сложения и умножения нечетких треугольных чисел следующим образом:
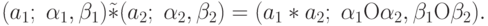
 — либо сложение, либо умножение,
— либо сложение, либо умножение,  — некоторая бинарная операция,
определенная на множестве неотрицательных действительных чисел.
— некоторая бинарная операция,
определенная на множестве неотрицательных действительных чисел.Опишем, какими свойствами должна обладать операция  для того,
чтобы сложение и умножение были коммутативны, ассоциативны, дистрибутивны, а также
существовали противоположные и обратные элементы.
для того,
чтобы сложение и умножение были коммутативны, ассоциативны, дистрибутивны, а также
существовали противоположные и обратные элементы.
Очевидно, что для того, чтобы операция  была коммутативной и
ассоциативной,
была коммутативной и
ассоциативной,  также должна быть коммутативной и ассоциативной, т.е. удовлетворять следующим
условиям:
также должна быть коммутативной и ассоциативной, т.е. удовлетворять следующим
условиям:
 |
( 1) |
Пусть 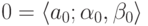 — нечеткий
ноль. Очевидно, что его мода
— нечеткий
ноль. Очевидно, что его мода 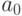 равна нулю, а коэффициенты
размытости
равна нулю, а коэффициенты
размытости 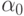 ,
и
,
и 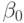 фиксированные значения. Тогда для любого
фиксированные значения. Тогда для любого 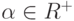 имеем
имеем

Для того, чтобы каждое нечеткое число обладало противоположным,
необходимо, чтобы для любого 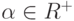 существовали
существовали 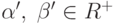 , такие,
что
, такие,
что

Аналогично, если  —
нечеткая единица, то для любого
—
нечеткая единица, то для любого 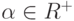 имеем
имеем

И для любого 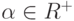 существуют
существуют  ,
такие, что
,
такие, что
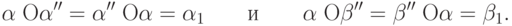
Легко заметить, что алгебраическая система 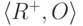 образует абелеву группу. Следовательно,
образует абелеву группу. Следовательно,  и для любого
и для любого 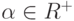 имеем
имеем  .
.
Для того, чтобы операции 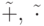 удовлетворяли
условию
дистрибутивности, необходимо и достаточно, чтобы для любых
удовлетворяли
условию
дистрибутивности, необходимо и достаточно, чтобы для любых 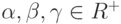 операция
операция  удовлетворяла следующему условию:
удовлетворяла следующему условию:
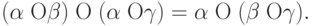 |
( 2) |
Если  коммутативна и ассоциативна, то получим
коммутативна и ассоциативна, то получим

Следовательно, для того, чтобы условие (2) выполнялось, достаточно,
чтобы  была коммутативна, ассоциативна и идемпотентна, т.е.
удовлетворяла условиям (1) и для любого
была коммутативна, ассоциативна и идемпотентна, т.е.
удовлетворяла условиям (1) и для любого 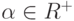
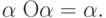
Нетрудно показать, что никакая группа не обладает свойством идемпотентности.
Вывод
Невозможно построить арифметику нечетких треугольных чисел, изоморфную арифметике действительных (четких) чисел, если размытость суммы и произведения нечетких треугольных чисел вычисляется по одному алгоритму.
Теперь рассмотрим случай, когда размытость суммы и произведения определяются по разным алгоритмам. Пусть

Очевидно, что если алгебраическая система  удовлетворяет свойствам коммутативности, ассоциативности, дистрибутивности,
существования нейтрального и единичного элементов, существования
противоположного и обратного
элементов, то она образует ассоциативное, коммутативное кольцо с единицей и с
делением (т.е. почти поле).
удовлетворяет свойствам коммутативности, ассоциативности, дистрибутивности,
существования нейтрального и единичного элементов, существования
противоположного и обратного
элементов, то она образует ассоциативное, коммутативное кольцо с единицей и с
делением (т.е. почти поле).
Пример.
Рассмотрим поле 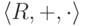 действительных
чисел. Функция
действительных
чисел. Функция  является взаимно однозначным
отображением
является взаимно однозначным
отображением 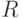 на
на  .
Определим операции
.
Определим операции  и
и  таким образом,
чтобы
таким образом,
чтобы  являлось
изоморфизмом соответствующих систем. Очевидно, что должны выполняться
следующие равенства:
являлось
изоморфизмом соответствующих систем. Очевидно, что должны выполняться
следующие равенства:

Таким образом, мы получим
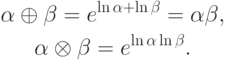
Нетрудно убедиться, что при таком задании операций размытости арифметика  будет коммутативной, ассоциативной и дистрибутивной. Роль нулевого элемента
будет выполнять нечеткое треугольное число
будет коммутативной, ассоциативной и дистрибутивной. Роль нулевого элемента
будет выполнять нечеткое треугольное число 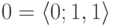 ;
роль единичного элемента — нечеткое треугольное число
;
роль единичного элемента — нечеткое треугольное число 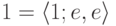 .
Для произвольного нечеткого треугольного числа
.
Для произвольного нечеткого треугольного числа 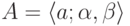 противоположным числом будет
противоположным числом будет  и обратным элементом будет
и обратным элементом будет  .
.
Недостатком этой арифметики является то, что в нее не входят четкие и "получеткие" числа, т.е. числа, у которых хотя бы один из коэффициентов размытости равен нулю. Но этого легко избежать, если доопределить ее, например, следующим образом:
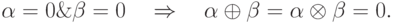
Заметим, что, варьируя мощность изоморфного поля, мы тем самым варьируем и мощность множества коэффициентов размытости, используемых в данной арифметике.

