| Казахстан, Алматы |
Рекурсивные функции
Примитивно рекурсивные множества
Будем называть множество примитивно рекурсивным, если его
характеристическая функция примитивно рекурсивна. (Вариант: если
оно является множеством нулей примитивно рекурсивной функции;
это то же самое, так как можно сделать подстановку в
функцию  .)
.)
Пересечение и объединение примитивно рекурсивных множеств примитивно рекурсивны (сложим или перемножим функции, множествами нулей которых они являются). Дополнение примитивно рекурсивного множества примитивно рекурсивно. Отождествляя множества со свойствами, можно сказать, что конъюнкции, дизъюнкции и отрицания примитивно рекурсивных свойств будут примитивно рекурсивны.
Свойства x=y и  примитивно рекурсивны
( x=y тогда и
только тогда, когда
примитивно рекурсивны
( x=y тогда и
только тогда, когда  ).
).
Функция f(x), заданная соотношением
f(x) = [ if R(x) then g(x) else h(x) fi ],
будет примитивно рекурсивной, если таковы функции g
и h и
свойство R. В самом деле, f(x) можно записать как  ,
где r
характеристическая
функция свойства R.
,
где r
характеристическая
функция свойства R.
Теперь можно записать формулу для прибавления единицы по модулю n (для чисел, меньших n ):
x+1 mod n = [ if x+1 = n then 0 else x+1 fi ]
После этого функцию x mod n (остаток от деления на n ) можно определить рекурсивно:
0 mod n = 0; (x+1) mod n = (x mod n) + 1 mod n.
Покажем, что ограниченные кванторы, примененные к примитивно рекурсивным свойствам (множествам), дают снова примитивно рекурсивные свойства. Это означает, например, что если свойство R(x,y) примитивно рекурсивно, то свойства
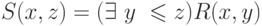
и
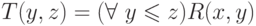
также примитивно рекурсивны. Чтобы убедиться в этом, заметим, что для функций ограниченный квантор соответствует перемножению или суммированию: если свойство R(x,y) равносильно r(x,y)=0, то
![S(x,z)\Leftrightarrow\left[\prod\limits_{y=0}^{z} r(x,y) = 0\right].](/sites/default/files/tex_cache/4719fa2c0d36deb0403b77792fbe9630.png)
А произведение легко определить рекурсивно:
![\begin{align*}
%
\prod\limits_{y=0}^{0} r(x,y)&= r(x,0);\\
\prod\limits_{y=0}^{t+1} r(x,y)&=
\left[\prod\limits_{y=0}^{t}r(x,y)\right]\cdot r(x,t+1);
%
\end{align*}](/sites/default/files/tex_cache/855e9237032d725c2e0192a3bb7a2fe1.png)
с суммированием можно поступить аналогичным образом.
После этого легко заметить, что свойство " быть простым" примитивно рекурсивно (число больше единицы, и любое меньшее число или меньше 2, или не является делителем).
Покажем теперь, что если график некоторой функции f примитивно
рекурсивен и ее значения ограничены сверху некоторой примитивно
рекурсивной функцией g, то сама функция f примитивно
рекурсивна. В самом деле, если r характеристическая
функция графика, то есть r(x,y)=1 при y=f(x)
и r(x,y)=0
при  (для простоты мы рассматриваем случай функций
одного аргумента), то
(для простоты мы рассматриваем случай функций
одного аргумента), то
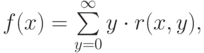
а суммирование можно ограничить сверху выражением g(x) и воспользоваться примитивной рекурсивностью ограниченной суммы.
Отсюда легко вывести следующее утверждение: если функция g и свойство R(x,y) примитивно рекурсивны, то функция x 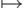 f(x) = наименьшее y <= g(x), для которого R(x,y) (если для некоторого x такого y нет, то полагаем значение функции равным, скажем, g(x)+1 ) будет примитивно рекурсивной. В самом деле, график функции f легко описать с помощью ограниченных кванторов.
f(x) = наименьшее y <= g(x), для которого R(x,y) (если для некоторого x такого y нет, то полагаем значение функции равным, скажем, g(x)+1 ) будет примитивно рекурсивной. В самом деле, график функции f легко описать с помощью ограниченных кванторов.
Такой способ определения функции называют ограниченным оператором минимизации в отличие от неограниченного, где нет заранее известной границы g(x). Как мы увидим, в неограниченном случае получающаяся функция не обязана быть примитивно рекурсивной.
Ограниченный оператор минимизации можно использовать, чтобы
убедиться, что функция x 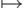 (минимальное
простое
число, большее x ) примитивно рекурсивна (рассуждение Евклида
о бесконечности множества простых чисел устанавливает, что это число не превосходит x!+1, а факториал
примитивно рекурсивен). После этого функция n
(минимальное
простое
число, большее x ) примитивно рекурсивна (рассуждение Евклида
о бесконечности множества простых чисел устанавливает, что это число не превосходит x!+1, а факториал
примитивно рекурсивен). После этого функция n 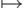 ( n -е простое число) легко определяется с помощью
рекурсии.
( n -е простое число) легко определяется с помощью
рекурсии.
Другие виды рекурсии
Слова " рекурсивное определение функции" можно понимать и в более широком смысле, нежели мы это делали (см. выше определение рекурсии, или примитивной рекурсии) как любой способ задания функции, который связывает значение функции в данной точке с другими ее значениями. Как мы увидим ниже при обсуждении функции Аккермана, есть такие схемы рекурсивных определений, которые выводят из класса примитивно рекурсивных функций. Но есть и такие, которые можно свести к рассмотренной нами схеме.
Мы приведем два примера последнего типа: совместное определение нескольких функций и использование произвольных меньших значений аргумента.
Совместная рекурсия. Пусть две одноместные функции f и g заданы соотношениями:
f(0) = a, g(0) = b, f(n+1) = F(n,f(n),g(n)), g(n+1) = G(n,f(n),g(n)),
где a и b некоторые числа, а функции F и G примитивно рекурсивные функции трех аргументов. Покажем, что тогда функции f и g примитивно рекурсивны.
Чтобы доказать это, нам потребуется примитивно рекурсивная
нумерация пар такая функция ![\langle x,y \rangle \hm\to [x,y]](/sites/default/files/tex_cache/f3393c87155db741ba54fd580dae01fa.png) (номер пары мы обозначаем квадратными скобками), которая была бы
примитивно рекурсивна вместе с двумя обратными функциями
(дающими по номеру пары ее первый и второй члены).
Тогда мы сможем написать рекурсивное определение для
функции h(n)=[f(n),g(n)]:
(номер пары мы обозначаем квадратными скобками), которая была бы
примитивно рекурсивна вместе с двумя обратными функциями
(дающими по номеру пары ее первый и второй члены).
Тогда мы сможем написать рекурсивное определение для
функции h(n)=[f(n),g(n)]:
h(0) = [a,b], h(n+1) = [F(n,p1(h(n)),p2(h(n))),G(n,p1(h(n)),p2(h(n)))],
где функции p1 и p2 дают по номеру пары первый и второй ее члены. Если функция h примитивно рекурсивна, то и функции f и g (композиции h с функциями p1 и p2 ) также примитивно рекурсивны.
Осталось объяснить, как найти примитивно рекурсивную нумерацию пар. Можно заметить, что есть многочлен второго порядка с двумя переменными, задающий взаимно однозначное соответствие N x N -> N. Это соответствие видно из таблицы:
6 3 7 1 4 8 0 2 5 9
Примитивную рекурсивность обратных отображений p1 и p2 можно установить, воспользовавшись ограниченной минимизацией, так как p1(n) есть минимальное x <= n, для которого найдется y <= n, при котором [x,y]=n.
Менее симметричная нумерация пар может быть задана формулой [a,b]=(2a+1)2b-1. Можно также заметить, что нам не нужно, чтобы все числа были номерами каких-то пар, и воспользоваться нумерацией [a,b]=2a3b.
Заметим в заключение, что аналогичная конструкция применима для большего числа одновременно определяемых функций и для функций от большего числа аргументов.
Возвратная рекурсия. Следующее утверждение показывает, что при рекурсивном определении можно использовать не только значение в предыдущей точке, но и любое предшествующее значение.
Теорема 74. Пусть функция g одного аргумента примитивно рекурсивна, причем g(x)<x при x>0 ; пусть F примитивно рекурсивная функция двух аргументов; пусть c произвольная константа. Тогда функция h, определенная соотношениями
h(0) = c, h(x) = F(x,h(g(x))) при x>0
примитивно рекурсивна.
Чтобы доказать эту теорему, используем следующую нумерацию конечных последовательностей натуральных чисел: номером пустой
последовательности считаем число 1, номером одноэлементной
последовательности  считаем
число 2a+1,
последовательность
считаем
число 2a+1,
последовательность 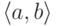 имеет
номер 2a+13b+1, последовательность
имеет
номер 2a+13b+1, последовательность  имеет номер 2a+13b+15c+1 и так далее (основания
степеней простые числа). Будем обозначать номер
последовательности
имеет номер 2a+13b+15c+1 и так далее (основания
степеней простые числа). Будем обозначать номер
последовательности  через [a,b,...,z]. Эта нумерация в некотором смысле примитивно
рекурсивна. Конечно, буквально это понимать нельзя, так как
нумерация представляет собой " функцию с переменным числом
аргументов". Но разные связанные с ней функции примитивно
рекурсивны. В частности, таковы функции
через [a,b,...,z]. Эта нумерация в некотором смысле примитивно
рекурсивна. Конечно, буквально это понимать нельзя, так как
нумерация представляет собой " функцию с переменным числом
аргументов". Но разные связанные с ней функции примитивно
рекурсивны. В частности, таковы функции
- Length(x) = длина последовательности с номером x ;
- Select(i,x)=i -ый член последовательности с номером x ;
- Append(x,y)= номер последовательности, которая получается приписыванием числа y к последовательности с номером x.
Все эти функции (и другие аналогичные) сводятся к различным операциям с простыми числами и множителями, которые мы в сущности уже разбирали.
Теперь мы докажем, что функция
![x \mapsto H(x)=[h(0),h(1),...,h(x)]](/sites/default/files/tex_cache/cdac2c0682f380b79e06050371ff8fa5.png)
примитивно рекурсивна. В самом деле, H(0)=[c], а
H(k+1)= Append(H(k),F(k+1,Select(g(k+1),H(k)))).

