| Россия |
Нейронные сети и ...
Нейронные сети и нечеткая логика
Системы нечеткой логики (fuzzy logics systems) могут оперировать с неточной качественной информацией и объяснять принятые решения, но не способны автоматически усваивать правила их вывода. Вследствие этого, весьма желательна их кооперация с другими системами обработки информации для преодоления этого недостатка. Подобные системы сейчас активно используются в различных областях, таких как контроль технологических процессов, конструирование, финансовые операции, оценка кредитоспособности, медицинская диагностика и др. Нейронные сети используются здесь для настройки функций принадлежности нечетких систем принятия решений. Такая их способность особенно важна при решении экономических и финансовых задач, поскольку вследствие их динамической природы функции принадлежности неизбежно должны адаптироваться к изменяющимся условиям.
Хотя нечеткая логика может явно использоваться для представления знаний эксперта с помощью правил для лингвистических переменных, обычно требуется очень много времени для конструирования и настройки функций принадлежности, которые количественно определяют эти переменные. Нейросетевые методы обучения автоматизируют этот процесс и существенно сокращают время разработки и затраты на нее, улучшая при этом параметры системы. Системы, использующие нейронные сети для определения параметров нечетких моделей, называются нейронными нечеткими системами. Важнейшим свойством этих систем является их интерпретируемость в терминах нечетких правил if-then.
Кроме них имеются также нечеткие нейронные системы. Так называются нейронные сети, использующие методы нечеткости для ускорения обучения и улучшения своих характеристик. Это может достигаться, например, использованием нечетких правил для изменения темпа обучения или же рассмотрением нейронных сетей с нечеткими значениями входов.
Предыдущий градиент  |
Текущий градиент | ||||
|---|---|---|---|---|---|
| NB | NS | Z | PS | PB | |
| NB | PB | PS | Z | NS | NB |
| NS | NS | PS | Z | NS | NB |
| Z | NB | NS | Z | NS | NB |
| PS | NB | NS | Z | PS | NS |
| PB | NB | NS | Z | PS | PB |
Лингвистические переменные Темп Обучения и Градиент принимают в иллюстрируемом таблицей нечетком правиле адаптации следующие значения: NB - большой отрицательный; NS - малый отрицательный; Z - близок к нулю; PS - малый положительный; PB - большой положительный.
Наконец, в современных гибридных нейронных нечетких системах нейронные сети и нечеткие модели комбинируются в единую гомогенную архитектуру. Такие системы могут интерпретироваться либо как нейронные сети с нечеткими параметрами, либо как параллельные распределенные нечеткие системы.
Элементы нечеткой логики
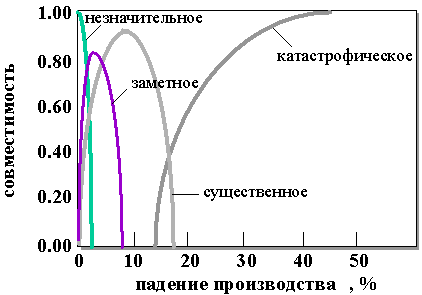
Центральным понятием нечеткой логики является понятие лингвистической переменной. Согласно Лотфи Заде лингвистической называется переменная, значениями которой являются слова или предложения естественного или искусственного языка. Примером лингвистической переменной является, например, падение производства, если она принимает не числовые, а лингвистические значения, такие как, например, незначительное, заметное, существенное, и катастрофическое. Очевидно, что лингвистические значения нечетко характеризуют имеющуюся ситуацию. Например, падение производства на 3% можно рассматривать и как в какой-то мере незначительное, и как в какой-то мере заметное. Интуитивно ясно, что мера того, что данное падение является катастрофическим должна быть весьма мала.
Смысл лингвистического значения X и характеризуется выбранной мерой - так называемой функций принадлежности (membership
function) ![\mu:\rightarrow[0,1]](/sites/default/files/tex_cache/6c50c485609f9d2a2a40233721c3e315.png) , которая каждому элементу u универсального множества U ставит в соответствие значение совместимости этого элемента с X .
В нашем случае универсальным множеством является множество всех возможных величин падения производства (от 0 до 100%).
, которая каждому элементу u универсального множества U ставит в соответствие значение совместимости этого элемента с X .
В нашем случае универсальным множеством является множество всех возможных величин падения производства (от 0 до 100%).
Нечеткое правило связывает значения лингвистических переменных. Примером такого правила может быть, например, следующее.
Если (падение производства - катастрофическое), то (доходы от экспорта энергоресурсов - значительные).
Нечеткое подмножество универсального множества U характеризуется функцией принадлежности ![mu_A:U\rightarrow[0,1]](/sites/default/files/tex_cache/98ee069172d82d8ca4ae47565dec6049.png) , которая ставит в соответствие
каждому элементу
, которая ставит в соответствие
каждому элементу 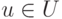 число
число 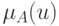 из интервала [0, 1], характеризующее степень принадлежности элемента u подмножеству A.
из интервала [0, 1], характеризующее степень принадлежности элемента u подмножеству A.
Носителем множества A называется множество таких точек в U, для которых величина 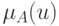 положительна.
положительна.