| Россия |
Нейросетевая оптимизация
Имитация отжига
В предыдущем разделе мы заметили, что переход от бинарных нейронов к аналоговым значительно улучшил свойства решения. Аналогичного
эффекта можно добиться используя по-прежнему бинарные нейроны, но заменив детерминистскую динамику стохастической, характеризуемой
некоторой эффективной температурой  . При этом среднее значение состояния нейрона также будет лежать в допустимом интервале
. При этом среднее значение состояния нейрона также будет лежать в допустимом интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
Положительная роль температуры заключается в том, что шум позволяет системе покидать локальные минимумы энергии и двигаться в сторону более глубоких энергетических минимумов. Соответствующий (не нейросетевой) алгоритм оптимизации был предложен в 1953 г. и получил название имитации отжига (Metropolis et al., 1953). Этот термин происходит от названия способа выжигания дефектов в кристаллической решетке. Атомы, занимающие в ней неправильное место, при низкой температуре не могут сместиться в нужное положение - им не хватает кинетической энергии для преодоления потенциального барьера. При этом система в целом находится в состоянии локального энергетического минимума. Для выхода из него металл нагревают до высокой температуры, а затем медленно охлаждают, позволяя атомам занять правильные положения в решетке, соответствующее глобальному минимуму энергии.
Субоптимальное решение некоторой задачи оптимизации, например, задачи коммивояжера, также может рассматриваться как решение в
котором имеются дефекты - неправильные части маршрута. Лин и Кернигэн (Lin & Kernigan, 1973) ввели элементарные операции изменения
текущего решения, такие как перенос (часть маршрута вырезается и вставляется в другое место) и обращение (выбирается фрагмент маршрута
и порядок прохождения городов в нем меняется на обратный). При применении одной из этих операций происходит изменение маршрута с  на
на 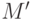 ,
и значение минимизируемого функционала меняется на
,
и значение минимизируемого функционала меняется на 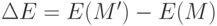 . В соответствии с принципами термодинамики, это изменение принимается с
вероятностью
. В соответствии с принципами термодинамики, это изменение принимается с
вероятностью
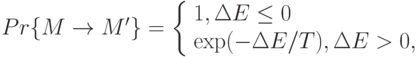
 - эффективная температура. Таким образом в методе отжига с некоторой вероятностью допускается переход системы в состояния с более
высокой энергией. Эта вероятность тем выше, чем выше эффективная температура. Поиск минимума начинается с некоторого начального маршрута
при высоком значении температуры. По мере эволюции состояния системы эта температура медленно снижается (для примера - на 5% после
осуществления
- эффективная температура. Таким образом в методе отжига с некоторой вероятностью допускается переход системы в состояния с более
высокой энергией. Эта вероятность тем выше, чем выше эффективная температура. Поиск минимума начинается с некоторого начального маршрута
при высоком значении температуры. По мере эволюции состояния системы эта температура медленно снижается (для примера - на 5% после
осуществления  элементарных операций изменения маршрута). Поиск продолжается до тех пор, пока система не захватывается энергетическим
минимумом, из которого она уже не может выйти за счет тепловых флуктуаций. Многочисленные исследования показали, что метод имитации
отжига является очень эффективным способом получения решений близких к оптимальному и часто служит эталоном сравнения для нейросетевых
подходов. Заметим, однако, что при реализации "в железе" нейросетевой подход все равно оказывается вне конкуренции по
скорости получения решения.
элементарных операций изменения маршрута). Поиск продолжается до тех пор, пока система не захватывается энергетическим
минимумом, из которого она уже не может выйти за счет тепловых флуктуаций. Многочисленные исследования показали, что метод имитации
отжига является очень эффективным способом получения решений близких к оптимальному и часто служит эталоном сравнения для нейросетевых
подходов. Заметим, однако, что при реализации "в железе" нейросетевой подход все равно оказывается вне конкуренции по
скорости получения решения.Метод эластичной сети
Иной подход к решению задачи коммивояжера использовали в 1987 году Дурбин и Уиллшоу (Durbin & Willshaw, 1987). Хотя они явно и не использовали в своей работе понятия искусственной нейронной сети, но в качестве отправной точки упоминали об аналогии с механизмами установления упорядоченных нейронных связей. Исследователи предложили рассматривать каждый из маршрутов коммивояжера как отображение окружности на плоскость, так что в каждый город на плоскости отображается некоторая точка этой окружности. При этом требуется, чтобы соседние точки на окружности отображались в точки, по возможности ближайшие и на плоскости. Алгоритм стартует с помещения на плоскость небольшой окружности (кольца), которая неравномерно расширяясь проходит практически около всех городов и, в конечном итоге, определяет искомый маршрут. Каждая точка расширяющегося кольца движется под действием двух сил: первая перемещает ее в сторону ближайшего города, а вторая смещает в сторону ее соседей на кольце так, чтобы уменьшить его длину. По мере расширения такой эластичной сети, каждый город оказывается ассоциирован с определенным участком кольца.
Вначале все города оказывают приблизительно одинаковое влияние на каждую точку маршрута. В последующем, большие расстояния
становятся менее влиятельными и каждый город становится более специфичным для ближайших к нему точек кольца. Такое постепенное
увеличение специфичности, которое, конечно, напоминает уже знакомый нам метод обучения сети Кохонена, контролируется значением
некоторого эффективного радиуса 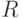 . Если обозначить через
. Если обозначить через 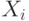 вектор, определяющий положение
вектор, определяющий положение  -го города на плоскости, а
-го города на плоскости, а 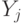 -координату
-координату 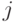 -й
точки на кольце, то закон изменения последней имеет вид
-й
точки на кольце, то закон изменения последней имеет вид
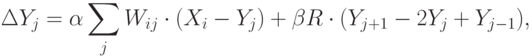
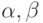 определяют относительное воздействие на точку
определяют относительное воздействие на точку 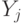 описанных выше двух сил. Коэффициенты
описанных выше двух сил. Коэффициенты 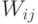 , определяющие воздействие
, определяющие воздействие  -го
города на
-го
города на 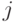 -ю точку кольца, являются функцией расстояния
-ю точку кольца, являются функцией расстояния 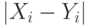 и параметра
и параметра 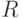 . Эти коэффициенты нормированы так, что полное воздействие
каждого из городов оказывается одинаковым:
. Эти коэффициенты нормированы так, что полное воздействие
каждого из городов оказывается одинаковым: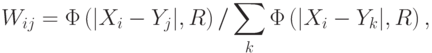
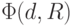 - положительная, ограниченная и убывающая функция d, приближающаяся к нулю при
- положительная, ограниченная и убывающая функция d, приближающаяся к нулю при  Если в качестве этой функции выбрать
распределение Гаусса
Если в качестве этой функции выбрать
распределение Гаусса 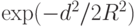 , то можно определить функцию Ляпунова
, то можно определить функцию Ляпунова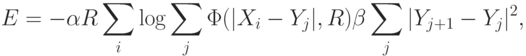
Дурбин и Уиллшоу показали, что для задачи с 30 городами, рассмотренной Хопфилдом и Танком, метод эластичной сети генерирует наикратчайший маршрут примерно за 1000 итераций. Для 100 городов найденный этим методом маршрут лишь на 1% превосходил оптимальный.

