Реализация булевых функций с помощью логических схем

Схемы и линейные программы

Указанное выше свойство характерно и для программ, в которых один раз вычисленное значение выражения можно использовать неоднократно. Рассмотрим один из простейших классов программ - линейные или неветвящиеся программы. Такие программы представляют последовательности присваиваний вида:

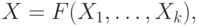
где X, X₁, ... , X_k - переменные, F - имя k -местной базисной функции.

В случае нашего базиса линейная программа состоит из присваиваний вида: 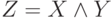, 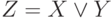и .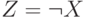

Линейная программа P с выделенными входными переменными X₁, ... , X_n порождает для каждого набора значений входных переменных естественный процесс вычисления: вначале переменным X₁, ... , X_n присваиваются значения , соответственно, а каждой из остальных переменных присваивается значение 0. Затем последовательно выполняются присваивания программы P, в результате чего каждая из переменных Z программы получит заключительное значение .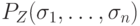

Определение 2.6. Скажем, что программа P со входными переменными X₁, ... , X_n вычисляет в выходной переменной Z функцию F(X₁, ..., X_n), если для любого набора значений входов после завершения работы .

Между схемами и линейными программами имеется тесная связь.

Теорема 2.1.

1. По каждой логической схеме S со входами x₁, ... , x_n и функциональными элементами v₁, ..., v_m можно эффективно построить линейную программу P_S со входными переменными x₁, ... , x_n и рабочими переменными v₁, ..., v_m, которая в любой переменной v_i, i=1,...,m, вычисляет функцию .
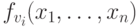2. По каждой линейной программе P со входными переменными X₁, ... , X_n, вычисляющей в выходной переменной Z некоторую функцию F(X₁, ..., X_n) можно эффективно построить логическую схему S_P со входами X₁, ... , X_n, в которой имеется вершина v такая, что f_v((X₁, ..., X_n) = F(X₁, ..., X_n).

Доказательство. (1) Пусть S - схема со входами x₁, ... , x_n и функциональными элементами v₁, ..., v_m. Построим по ней линейную программу P_S со входными переменными x₁, ... , x_n следующим образом. Упорядочим все входные и функциональные вершины S по глубине (вершины одной глубины в любом порядке): u₁, ..., u_n+m. Программа P_S будет последовательностью m присваиваний.

• Пусть вершина u_n+i помечена и в нее входит
• ребро из u_j. Тогда в качестве i -ой команды поместим в P_S присваивание .
• Пусть вершина u_n+i помечена и в нее входят ребра из u_j и u_k. Тогда в качестве i -ой команды поместим в P_S присваивание .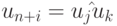

Упорядочение вершин по глубине гарантирует, что j <n+ i и k <n+ i. Поэтому при вычислении u_{n+i} значения аргументов уже получены и индукцией по глубине легко показать, что для каждого i=1,...,m программа P_S вычисляет в переменной v_i функцию .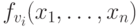

Доказательство пункта (2) проведите самостоятельно (см. задачу 2.1).

Пример 2.1. Применим конструкцию теоремы к схеме S₁, представленной на рис.2.1. Ее вершины можно упорядочить по глубине так: x, y, z, a, b, c, d, e, f. Порождая команды по описанным выше правилам, получим следующую линейную программу P_{S₁}:

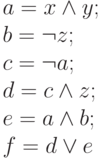
Замечание. Число команд в линейной программе P_S, т.е. время ее выполнения, совпадает со сложностью L(S) схемы S. Глубина схемы D(S) также имеет смысл с точки зрения времени вычисления. Именно, D(S) - это время выполнения P_S на многопроцессорной системе. Действительно, все команды, соответствующие вершинам одинаковой глубины, можно выполнять параллельно на разных процессорах, так как результаты любой из них не используются в качестве аргументов другой.