Работа со списками

3.2. Выявление структуры списков

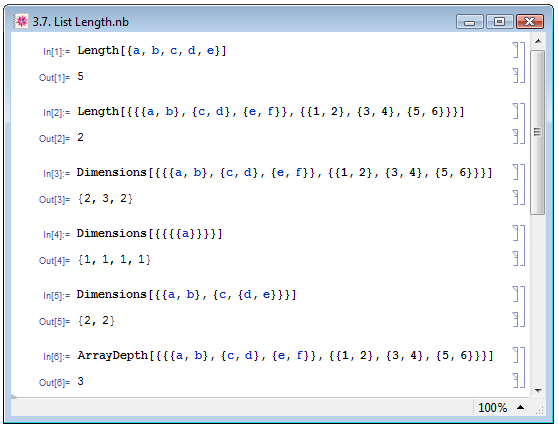
Списки относятся к данным сложной структуры. Поэтому при работе с ними возникает необходимость контроля над структурой, иначе применение списков может привести к грубым ошибкам, как явным, сопровождаемым выдачей сообщения об ошибке, так и неявным, на наличие которых Mathematica никаким образом не реагирует, но результаты расчётов оказываются неверными. Для выявления структуры списков в программе имеется ряд функций. Одна из них — Length. Она возвращает длину списка — число элементов списка. Если мы применим эту функцию к линейному (невложенному, не содержащему в качестве элементов других списков) списку, то мы получим число элементов, которое в нём содержится; для вложенных списков мы получим число внутренних списков в нём, при этом количество элементов в этих внутренних списках приниматься в расчёт не будет — см., соответственно, примеры In[1] и In[2] на рис. 3.7.

Если вложенный список полностью состоит из внутренних списков одинаковой длины, то всё-таки существует возможность получить информацию о длине внутренних списков: для этого следует воспользоваться функцией Dimensions. При помощи этой функции в примере In[3] на рис. 3.7 мы узнаём о том, что заданный список содержит два внутренних списка, каждый из которых сам состоит из трёх списков, содержащих по два элемента. Помогает нам функция Dimensions и в экзотическом случае, когда на каждом уровне вложенного списка содержится всего один элемент — пример In[4].

Если вложенный список list состоит из внутренних списков одинаковой длины только до определённого уровня n, то функция Dimensions поможет узнать структуру list только до этого уровня n включительно. Например, в трёхуровневом списке {{a,b},{c,{d,e}} на первом уровне находится два элемента, представляющих собой списки {a,b} и {c,{d,e}}. Каждый элемент-список также содержит по два элемента, которые являются элементами второго уровня: в первом случае — это символы a и b, а во втором — символ c и список {d,e}. На третьем уровне находятся только элементы списка {d,e}, очевидно, что символы a, b и c никаких элементов не содержат. Таким образом, для исходного списка количество элементов внутренних списков совпадает только до второго уровня включительно, и также до второго уровня этот список может быть описан функцией Dimensions. Таким образом, вычисление выражения Dimensions[{{a,b},{c,{d,e}}] вернёт в выходной ячейке Out выражение {2,2}. Справедливость наших рассуждений подтверждается примером In[5] на рис. 3.7.

Если вложенный список состоит из списков одинаковой длины, то для того, чтобы определить глубину этого вложенного списка, то есть, число уровней, на которое необходимо спуститься, чтобы добраться до выражения, не являющегося списком, используется функция ArrayDepth — пример In[6] на рис. 3.7.

Подробней о получении информации о длине и глубине списков см. книгу П. Веллина и др. [14, с. 58–59].

Рис. 3.7. Определение структуры линейных и вложенных списков

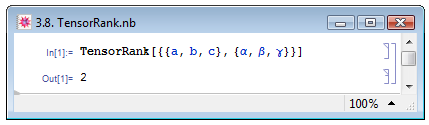
Если список expr является тензором, то функция TensorRank[expr] позволяет определить ранг этого тензора — рис. 3.8.

Рис. 3.8. Определение ранга тензора

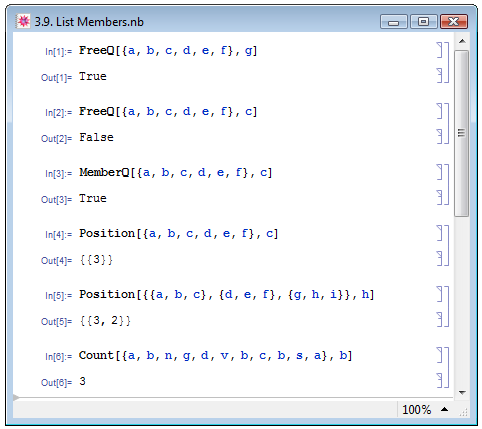
Крайне полезной в Mathematica является возможность проверять списки на содержание тех или иных выражений. Так функция FreeQ[list,form] возвращает True, если список list НЕ содержит выражения form; также в пакете имеется в некоторой мере дублирующая функция MemberQ[list,form], которая напротив возвращает True, если список list содержит выражение form (см. примеры In[1], In[2] и In[3] на рис. 3.9). А функция Position[list,form] возвращает позицию искомого элемента form в списке list. В нашем примере In[4] буква c занимает позицию с номером 3. Если список list не содержит выражения form, то возвращается пустой список {}.

Эта же функция поможет нам, если мы хотим узнать позицию того или иного выражения во вложенном списке. Отличие будет лишь в представлении результата. В примере In[5] на рис. 3.9 буква h занимает позицию под номером 2 в третьем элементе вложенного списка.

Узнать, сколько раз некоторый элемент elem встречается в списке list, можно с помощью функции Count[list,elem]. Если список list не содержит выражения elem, то Count возвращает 0. Так в примере In[6] на рис. 3.9 мы выяснили, что символ b содержится в заданном списке 3 раза.

Рис. 3.9. Проверка списка на содержание в нём заданных выражений

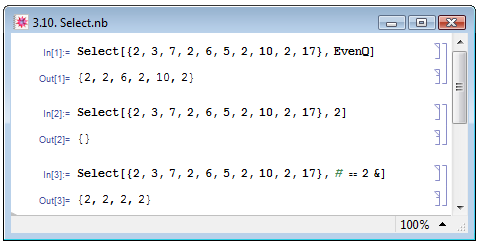
Ещё одна функция Select[list,cond] позволяет выбирать элементы списка list, возвращающие True при применении к ним предиката cond. В примере In[1] на рис. 3.10 из списка выбираются только чётные числа.

Для того чтобы выбрать из списка list только одинаковые элементы elem, недостаточно просто указать elem вместо условия cond: в этом случае будет просто сгенерирован пустой список (см. пример In[2] на рис. 3.10). Для этого следует задать условие с использованием анонимной функции в виде #==elem&. Так в примере In[3] мы выбираем из исходного списка только двойки. С анонимными функциями мы подробней познакомимся в лекции 9 настоящего курса, посвящённой функциональному программированию.

Если условию cond не соответствует ни один элемент списка list, то Select[list,cond] генерирует пустой список.

Подробней о функциях проверки содержания списка см. книгу П. Веллина и др. [14, с. 60–61].

Рис. 3.10. Выбор элементов списка по условию