|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Информационная безопасность. Стандарты и алгоритмы шифрования
Эффективность системы шифрования определяется числом кодовых комбинаций или ключей, которое необходимо перебрать, чтобы прочесть зашифрованный текст. Существует две системы ключей шифрования/дешифрования. Для симметричных алгоритмов предполагается, что ключ дешифрования может быть вычислен по известному ключу шифрования. Оба ключа при этом должны быть секретными (например, система DES). Отправитель и получатель должны знать ключи до начала обмена (эти ключи могут и совпадать). Набор таких ключей может быть достаточно большим и в процессе инициализации осуществляется выбор пары ключей, которые будут использованы в данной сессии. В общем случае могут использоваться довольно большие кодовые таблицы, но такая схема неудобна для многоточечного обмена.
Шифры бывают поточными и блочными. В первом случае обработка исходного текста производится побитно или побайтно. Во втором — текст перед обработкой разбивается на блоки.
Асимметричные схемы шифрования/дешифрования предполагают существование независимых ключей для шифрования и дешифрования, причем один не может быть получен из другого и наоборот. В идеале ключ дешифровки не может быть получен из шифрующего ключа за любое разумное время. В этом случае ключ шифрования может быть сделан общедоступным (например, алгоритм RSA ). Партнеры до начала коммуникаций должны послать друг другу ключи шифрования КШО и КШП (ключи шифрования отправителя и получателя). Возможность перехвата таких ключей опасности не представляет. Дешифрование выполняется с помощью ключей КДО и КДП, которые образуют пары с КШО и КШП соответственно и формируются совместно. Ключи КШО и КШП обычно пересылаются на фазе инициализации сессии информационного обмена.
Шифрование может осуществляться по определенным правилам с помощью таблиц шифрования или ключей. При этом могут использоваться самые разные алгоритмы, в том числе, например, перемещение символов текста определенным образом. За свою историю люди придумали достаточно большое число способов шифрования. Новейшие из них базируются на методиках, заимствованных из теории чисел.
Наиболее современные системы шифрования используют асимметричные алгоритмы с открытым и секретным ключами, где нет проблемы безопасной транспортировки ключа. К числу таких систем относится алгоритм RSA (Rivest-Shamir-Adleman — разработчики этой системы — Рональд Ривест, Ади Шамир и Леонард Адлеман, 1977 год), базирующийся на сложности разложения больших чисел на множители.
Другие сходные алгоритмы применяют целочисленные логарифмы и вычисление корней уравнений. В отличие от других систем, эти позволяют кроме шифрования эффективно идентифицировать отправителя (электронная подпись). К системам с открытым ключом предъявляются следующие требования:
- зашифрованный текст трудно (практически невозможно) расшифровать с использованием открытого ключа;
- восстановление закрытого ключа на основе известного открытого должно быть не реализуемой на современных ЭВМ задачей. При этом должна существовать объективная оценка нижнего предела числа операций, необходимых для решения такой задачи.
К сожалению, эти алгоритмы достаточно медленно работают. По этой причине они могут использоваться для транспортировки секретных ключей при одном из традиционных методов шифрования-дешифрования.
Но следует помнить, что не существует абсолютных мер защиты. На рис. 14.1 показан способ нарушения конфиденциальности в системах с двухключевой схемой шифрования.
Если хакер умудрится вставить свою ЭВМ в разрыв канала, соединяющего субъектов А и В, у него появляется возможность перехватывать в том числе и шифрованные сообщения. Пусть субъект А сформировал пару ключей К1А и К2А (ключ с индексом 2 является секретным), аналогичную пару ключей сгенерировал субъект В ( К1В и К2В ). Хакер же тем временем подготовил две пары ключей ( К1ХА: К2ХА и К1ХВ: К2ХВ ). Когда субъект А пошлет открытый ключ К1А субъекту В, хакер его подменит ключом К1ХА. Аналогичную процедуру он проделает с ключом К1В, посланным от В к А. Теперь сообщение А к В, зашифрованное с помощью ключа К1ХА, будет послано В. Хакер его перехватывает, дешифрует с помощью ключа К2ХА, шифрует с помощью ключа К1В и посылает В. Субъект В, получив послание, дешифрует его с помощью своего секретного ключа К2В. Аналогичная процедура будет проведена и при посылки сообщения от В к А. В сущности, единственным параметром, который изменится существенным образом, будет время доставки сообщения, так как это время будет включать дешифровку и повторную шифровку сообщения. Но при использовании быстродействующей ЭВМ и при работе с традиционной электронной почтой это может оказаться незаметным. Понятно, что между А и В появится дополнительный шаг (hop). Но и это может быть легко замаскировано под прокси сервер или Firewall.
Решить проблему подмены ключей можно путем пересылки открытого ключа своему партнеру по какому-то альтернативному каналу или сверки его по телефону. Для контроля достоверности ключа можно использовать сертификаты.
Начиная с 1997 года NIST (National Institute for Standards and Technology) совместно с промышленностью и криптографическим сообществом разрабатывал преемника для алгоритма DES (длина ключа 56 бит). В результате был создан алгоритм AES (Advanced Encryption Standard), который был опубликован в 2001 году (FIPS 197). AES представляет собой блочный, симметричный алгоритм шифрования с длиной блока 128 бит. Длина ключа может принимать значения 128, 192 или 256 бит (AES-128, AES-192 и AES-256, соответственно). Если предположить, что ключ DES можно подобрать за секунду, то для подбора ключа AES-128 потребуется около 149 триллионов лет (кстати, возраст нашей вселенной всего 20 миллиардов лет). Кроме AES ISO/IEC 18033 (см. http://www.ni.dm.de, http://csrc.nist.gov и http://www.x9.org) специфицирует еще шесть различных блочных шифров (см. таблицу 14.2.)
Базовые характеристики блочных алгоритмов шифрования представлены в таблице 14.3 (смотри http://book.itep.ru/6/idea_647.htm, ~6/des_641.htm и ~6/safr_648.htm).
| Название алгоритма | Размер блока данных | Длина ключа |
|---|---|---|
| DES | 64 | 56 |
| ГОСТ 28147-89 | 64 | 256 |
| SAFER+ | 128 | 128/192/256 |
| IDEA | 64 | 52*16 |
Относительные уровни безопасности разных алгоритмов представлены в таблице 14.4.
Стандарт на хэш функции задает документ ISO/IEC 10118. Эти хэш функции (см. табл. 14.5) используются практически во всех видах электронных подписей (ISO/IEC 14888). К сожалению, не существует международного стандарта для управления информационными системами безопасности.
В настоящее время имеется три семейства криптосистем с открытым ключом.
- Системы IF (Integer Factorization — целочисленная факторизация), такие, как система цифровой подписи, базирующаяся на RSA, использует сложность факторизации при работе с большими целыми числами.
- Системы DL (Discrete Logarithm — целочисленный логарифм), такие, как алгоритм цифровой подписи NIST (DSA, FIPS 186), базируются на вычислительной сложности оперирования с целочисленными логарифмами.
- Системы EC (Elliptic Curve эллиптические кривые) являются сходными с DL-примитивами. Они основываются на вычислительной сложности проблемы расчета целочисленных логарифмов через эллиптические кривые. Преимуществом этой системы является относительная ее сила по отношению к длине параметра. Другими словами, эллиптические кривые предоставляют большую секретность на бит.
Прочность всех этих алгоритмов основывается на трудностях, например, разложения больших чисел на сомножители или работы с целочисленными логарифмами. До сих пор не доказано, что не существует алгоритмов быстрого решения указанных проблем. Если такие алгоритмы будут найдены, придется придумывать другие системы шифрования.
Согласно закону Мура, плотность компонентов на чип удваивается каждые 18 месяцев. Это можно интерпретировать как удвоение вычислительной мощности ЭВМ каждые 18 месяцев.
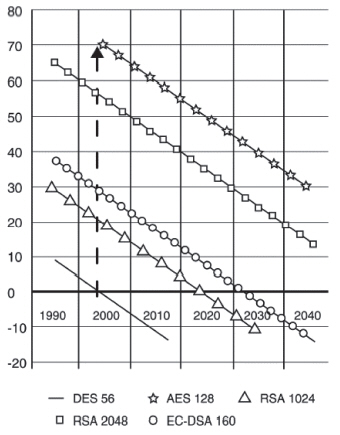
Развитие методов программирования и повышение быстродействия ЭВМ приводит к понижению надежности систем шифрования. Симметричные шифры теряют один бит безопасности в год. Хэш-функции и схемы, основанные на эллиптических кривых (ISO/IEC 15946-2), теряют два бит безопасности в год. RSA -схемы теряют 30 бит безопасности в год. На рис. 14.2 показана временная зависимость деградации безопасности шифров (см. Network Security, V2004, Issue 12, декабрь 2004, стр. 6-11).
Полезную информацию по системам шифрования можно получить на следующих серверах:
- http://www.cs.hut.fi/crypto/
- http://www.subject.com/crypto/crypto.html
- http://www.rsa.com/
- http://www.netscape.com/newsref/ref/rsa.html
- http://www.microsoft.com/workshop/prog/security/pkcb/crypt.htm
- http://www.semper.org/sirene/people/gerrit/secprod.html
- http://www.fri.com/~rcv/deschall.htm
- http://www.cl.cam.ac.uk/brute/
Но прежде чем использовать тот или иной метод криптографии, следует понять:
- Полная безопасность невозможна, и обычно приходится находить компромисс между безопасностью и удобством работы.
- Информационная безопасность должна быть встроена в документооборот предприятия и соответствовать общей политике безопасности.
Из числа широко используемых приложений можно выделить безопасную электронную почту PGP (Pretty Good Privacy, см. http://book.itep.ru/6/pgp_644.htm), которая базируется на двух ключевой системе шифрования RSA и алгоритме IDEA (International Data Encryption Algorithm).
Но наиболее важным приложением современной криптографии являются электронные платежные системы (например, протокол SET, см. http://book.itep.ru/4/6/set_66.htm) и кредитные smart-карты. Несколько особняком стоят электронные монеты, формирование которых базируется формировании кодов с кратными хэш-совпадениями. Современный документооборот немыслим без электронных подписей.