Основные алгебраические структуры и операции
Характеризация инъективных, сюръективных и биективных отображений (в терминах произведений отображений)
Теорема 1.8.1.
Пусть 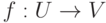 - отображение непустых множеств. Тогда:
- отображение непустых множеств. Тогда:
-
f - инъективное отображение тогда и только тогда, когда существует отображение
 такое, что gf=1U (т. е. существует левый обратный элемент для отображения f ),
такое, что gf=1U (т. е. существует левый обратный элемент для отображения f ), -
f - сюръективное отображение тогда и только тогда, когда существует отображение
 такое, что fg=1V (т. е. существует правый обратный элемент для отображения f ),
такое, что fg=1V (т. е. существует правый обратный элемент для отображения f ), -
f - биективное отображение тогда и только тогда, когда существует отображение
 такое, что gf=1U и fg=1V (т. е. существует левый и правый обратные для отображения f ).
такое, что gf=1U и fg=1V (т. е. существует левый и правый обратные для отображения f ).
Доказательство.
1а) Пусть 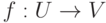 - инъективное отображение. Построим отображение
- инъективное отображение. Построим отображение  следующим образом. Если
следующим образом. Если 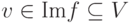 и v=f(u),
и v=f(u), 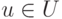 , то этот элемент u определен единственным образом (в силу инъективности отображения f ). В этом случае положим g(v)=u.
Для всех элементов
, то этот элемент u определен единственным образом (в силу инъективности отображения f ). В этом случае положим g(v)=u.
Для всех элементов  положим
положим  , где u0 - некоторый фиксированный элемент в U. Тогда для всякого элемента
, где u0 - некоторый фиксированный элемент в U. Тогда для всякого элемента 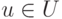 имеем (gf)(u)=g(f(u))=u=1U(u),
т. е. gf=1U.
имеем (gf)(u)=g(f(u))=u=1U(u),
т. е. gf=1U.
1б) Если существует отображение  такое, что gf=1U, и f(u1)=f(u2) для
такое, что gf=1U, и f(u1)=f(u2) для 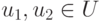 , то u1=1U(u1)=(gf)(u1)=g(f(u1))=g(f(u2))=(gf)(u2)=1U(u2)=u2.
Итак, f - инъективное отображение.
, то u1=1U(u1)=(gf)(u1)=g(f(u1))=g(f(u2))=(gf)(u2)=1U(u2)=u2.
Итак, f - инъективное отображение.
2а) Пусть 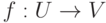 - сюръективное отображение. Для каждого элемента
- сюръективное отображение. Для каждого элемента 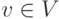 множество
множество  не является пустым. Выберем в нем один элемент uv (для интересующихся аксиоматикой теории множеств: это можно сделать в силу аксиомы выбора). Определим отображение
не является пустым. Выберем в нем один элемент uv (для интересующихся аксиоматикой теории множеств: это можно сделать в силу аксиомы выбора). Определим отображение  , полагая g(v)=uv. Тогда (fg)(v)=f(g(v))=f(uv)=v=1V(v).
Таким образом, fg=1V.
, полагая g(v)=uv. Тогда (fg)(v)=f(g(v))=f(uv)=v=1V(v).
Таким образом, fg=1V.
2б) Если fg=1V для некоторого отображения  , то для всякого
, то для всякого 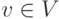 имеем v=1V(v)=(fg)(v)=f(g(v)),
т. е. v=f(u) для u=g(v), следовательно,
имеем v=1V(v)=(fg)(v)=f(g(v)),
т. е. v=f(u) для u=g(v), следовательно, 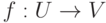 - сюръективное отображение.
- сюръективное отображение.
3а) Если 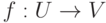 - биекция, то для всякого элемента
- биекция, то для всякого элемента 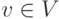 существует, и единственный, элемент
существует, и единственный, элемент 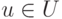 такой, что v=f(u). В этом случае положим g(v)=u. Получим отображение
такой, что v=f(u). В этом случае положим g(v)=u. Получим отображение  , для которого: (gf)(u)=g(f(u))=u
для всякого
, для которого: (gf)(u)=g(f(u))=u
для всякого 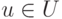 , т. е. gf=1U ; (fg)(v)=f(g(v))=f(g(f(u)))=f(u)=v
для всякого
, т. е. gf=1U ; (fg)(v)=f(g(v))=f(g(f(u)))=f(u)=v
для всякого 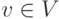 , т. е. fg=1V.
, т. е. fg=1V.
Замечание 1.8.2. Можно было воспользоваться уже доказанными утверждениями 1а), 2а): из инъективности отображения 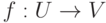 следует существование отображения
следует существование отображения  , для которого gf=1U ; из сюръективности отображения
, для которого gf=1U ; из сюръективности отображения 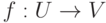 следует существование отображения
следует существование отображения 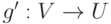 , для которого fg'=1V ; но тогда g'=1Ug'=(gf)g'=g(fg')=g1V=g; таким образом, gf=1U, fg=1V.
, для которого fg'=1V ; но тогда g'=1Ug'=(gf)g'=g(fg')=g1V=g; таким образом, gf=1U, fg=1V.
3б) Если существует отображение  , для которого gf=1U и fg=1V, то в силу 1б), f - инъекция, а в силу 2б), f - сюръекция, т. е. f - биекция.
, для которого gf=1U и fg=1V, то в силу 1б), f - инъекция, а в силу 2б), f - сюръекция, т. е. f - биекция.
Замечание 1.8.3. Отображение g, для которого gf=1U, fg =1V, как мы показали, определено однозначно. Оно будет обозначаться  .
.
Лемма 1.8.4. Пусть 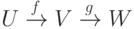 .
.
- Если f, g - инъекции, то gf - инъекция.
- Если f, g - сюръекции, то gf - сюръекция.
- Если f, g - биекции, то gf - биекция.
- Если f - биекция, то отображение
 - биекция.
- биекция.
Доказательство.


 , то
, то 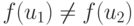 , и
, и  , т. е.
, т. е. 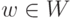 , то
, то  , и поэтому
, и поэтому