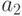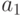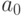|
Не очень понятно про оболочечные Данные,ячейки памяти могут наверно размер менять,какое это значение те же операции только ячейки больше,по скорости тоже самое |
Работа с числами в языке Java
4.2. Побитовые маски и сдвиги
| Оператор | Название | Пример | Примечание |
|---|---|---|---|
| ~ | Оператор побитового дополнения (побитовое "не", побитовое отрицание) | ~i | |
| ^ | Оператор " побитовое исключающее или" (XOR) | i^j | |
| & | Оператор "побитовое и" (AND) | i&j | |
| | | Оператор "побитовое или" (OR) | i|j |
| << | Оператор левого побитового сдвига |
| >>> | Оператор беззнакового правого побитового сдвига |
| >> | Оператор правого побитового сдвига с сохранением знака отрицательного числа |
| &= | y&=x эквивалентно y=y&x |
| |= | y|=x эквивалентно y=y|x |
| ^= | y^=x эквивалентно y=y^x |
| >>= | y>>=x эквивалентно y= y>>x |
| >>>= | y>>>=x эквивалентно y= y>>>x |
| <<= | y<<=x эквивалентно y= y<<x |
Побитовые операции – когда целые числа рассматриваются как наборы бит, где 0 и 1 играют роли логического нуля и логической единицы. При этом все логические операции для двух чисел осуществляются поразрядно – k-тый разряд первого числа с k-тым разрядом второго. Для простоты мы будем рассматривать четырехбитовые ячейки, хотя реально самая малая по размеру ячейка восьмибитовая и соответствует типу byte.
- а) установка в числе a нужных бит в 1 с помощью маски m операцией a|m (арифметический, или, что то же, побитовый оператор OR ).
Пусть число
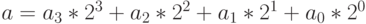 , где значения
, где значения 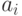 – содержание соответствующих бит числа (то есть либо нули , либо единицы).
– содержание соответствующих бит числа (то есть либо нули , либо единицы).Видно, что независимо от начального значения в числе a в результате нулевой и второй бит установились в единицу. Таким образом, операцию OR с маской можно использовать для установки нужных бит переменной в единицу, если нужные биты маски установлены в единицу, а остальные – нули.
- б) установка в числе a нужных бит в 0 с помощью маски m операцией a&m (арифметический, или, что то же, побитовый оператор AND ):
Видно, что независимо от начального значения в числе a в результате первый и третий бит установились в нуль. Таким образом, операцию AND с маской можно использовать для установки нужных бит переменной в ноль, если нужные биты маски установлены в ноль, а остальные – единицы.
-
в) инверсия (замена единиц на нули, а нулей на единицы) в битах числа a, стоящих на задаваемых маской m местах, операцией a^m (арифметический, или, что то же, побитовый оператор XOR ):
Видно, что если в бите, где маска m имеет единицу, у числа a происходит инверсия: если стоит 1, в результате будет 0, а если 0 – в результате будет 1. В остальных битах значение не меняется.
Восстановление первоначального значения после операции XOR – повторное XOR с той же битовой маской:
Видно, что содержание ячейки приняло то же значение, что было первоначально в ячейке a. Очевидно, что всегда (a ^ m) ^ m = a, так как повторная инверсия возвращает первоначальные значения в битах числа. Операция XOR часто используется в программировании для инверсии цветов частей экрана с сохранением в памяти только информации о маске. Повторное XOR с той же маской восстанавливает первоначальное изображение. - Имеется команда перевода вывода графики в режим XOR при рисовании, для этого используется команда graphics.setXORMode(цвет).
Еще одна область, где часто используется эта операция - криптография.
Инверсия всех битов числа осуществляется с помощью побитового отрицания ~a.
Побитовые сдвиги "<<", ">>" и ">>>" приводят к перемещению всех бит ячейки, к которой применяется оператор, на указанное число бит влево или вправо. Сначала рассмотрим действие операторов на положительные целые числа.
Побитовый сдвиг на n бит влево m<<n эквивалентен быстрому целочисленному умножению числа m на 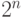 . Младшие биты (находящиеся справа), освобождающиеся после сдвигов, заполняются нулями. Следует учитывать, что старшие биты (находящиеся слева), выходящие за пределы ячейки, теряются, как и при обычном целочисленном переполнении.
. Младшие биты (находящиеся справа), освобождающиеся после сдвигов, заполняются нулями. Следует учитывать, что старшие биты (находящиеся слева), выходящие за пределы ячейки, теряются, как и при обычном целочисленном переполнении.
Побитовые сдвиги на n бит вправо m>>n или m>>>n эквивалентны быстрому целочисленному делению числа m на 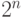 . При этом для положительных m разницы между операторами ">>" и ">>>" нет.
. При этом для положительных m разницы между операторами ">>" и ">>>" нет.
Рассмотрим теперь операции побитовых сдвигов для отрицательных чисел m. Поскольку они хранятся в дополнительном коде, их действие нетривиально. Как и раньше, для простоты будем считать, что ячейки четырехбитовые, хотя на деле побитовые операции проводятся только для ячеек типа int или long, то есть для 32-битных или 64-битных чисел.
Пусть m равно -1. В этом случае 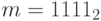 . Оператор
. Оператор  даст
даст 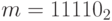 , но из-за четырехбитности ячейки старший бит теряется, и мы получаем
, но из-за четырехбитности ячейки старший бит теряется, и мы получаем 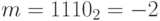 . То есть также получается полная эквивалентность умножению m на
. То есть также получается полная эквивалентность умножению m на 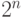 .
.
Иная ситуация возникает при побитовых сдвигах вправо. Оператор правого сдвига ">>" для положительных чисел заполняет освободившиеся биты нулями, а для отрицательных - единицами. Легко заметить, что этот оператор эквивалентен быстрому целочисленному делению числа m на 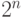 как для положительных, так и для отрицательных чисел. Оператор m>>>n, заполняющий нулями освободившиеся после сдвигов биты, переводит отрицательные числа в положительные. Поэтому он не может быть эквивалентен быстрому делению числа на
как для положительных, так и для отрицательных чисел. Оператор m>>>n, заполняющий нулями освободившиеся после сдвигов биты, переводит отрицательные числа в положительные. Поэтому он не может быть эквивалентен быстрому делению числа на 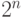 . Но иногда такой оператор бывает нужен для манипуляции с наборами бит, хранящихся в числовой ячейке. Само значение числа в этом случае значения не имеет, а ячейка используется как буфер соответствующего размера.
. Но иногда такой оператор бывает нужен для манипуляции с наборами бит, хранящихся в числовой ячейке. Само значение числа в этом случае значения не имеет, а ячейка используется как буфер соответствующего размера.
Например, можно преобразовать последовательность бит, образующее некое целое значение, в число типа float методом Float.intBitsToFloat(целое значение) или типа double методом Double.intBitsToDouble (целое значение). Так, Float.intBitsToFloat(0x7F7FFFFF) даст максимальное значение типа float.