Оценка производительности кластерных систем

4.2. Стандартные тесты производительности

4.2.1. Linpack benchmark

Первым тестом, о котором пойдет речь в этом разделе, является тест Linpack. Этот тест в настоящее время является практически стандартом де-факто в тестировании вычислительных систем - по крайней мере, список 500 наиболее высокопроизводительных систем мира (www.top500.org) составляется именно по результатам этого теста.

4.2.1.1. История теста

Тест Linpack, впервые был опубликован в 1979 г. и первоначально являлся дополнением к одноименной библиотеке численных методов, содержащей набор процедур для решения систем линейных алгебраических уравнений (СЛАУ) и предназначался для оценки времени решения той или иной системы с помощью этой библиотеки. Linpack является классическим примером теста-ядра (причем, поскольку к решению тех или иных СЛАУ сводятся очень многие реальные расчетные задачи - измеренные им характеристики являются в высокой степени репрезентативными).

Автором теста является Джек Донгарра (J. Jack Dongarra) из Университета штата Теннесси (до этого он сотрудничал с Аргоннской национальной лабораторией, где и была сформирована концепция тестов Linpack).

Тест состоит в решении системы линейных арифметических уравнений вида

Ax=f

методом LU-факторизации c выбором ведущего элемента столбца, где A - плотно заполненная матрица размерности N (первоначальный, "классический" вариант Linpack решал задачу размерности 100). Производительность в тесте Linpack измеряется в количестве производимых операций с плавающей запятой в секунду. Единицей измерения является 1 флопс, то есть одна такая операция в секунду. Поскольку количество операций, необходимое для решения задачи Linpack, известно с самого начала и зависит от ее размерности, измеряемая характеристика производительности получается как простое частное от деления этого известного числа операций на время, затраченное на решение задачи.

С течением времени и увеличении вычислительной мощности компьютеров, размерность теста Linpack была увеличена до 1000. Однако с появлением все более мощных вычислительных систем и эта размерность стала чересчур малой, более того, для тестирования кластерных систем была создана отдельная версия теста (доступная на сайте http://www.netlib.org/benchmark/hpl/) в которой размерность матрицы (и некоторые другие параметры) не являются фиксированными, а задаются пользователем теста.

Дело в том, что при увеличении размерности матрицы решаемой задачи, растет степень параллелизма, что может привести к увеличению производительности. Другим важным параметром, влияющим на производительность, является размер блока, с которым матрица распределяется между узлами кластерной системы. Особую значимость этот параметр имеет для компьютеров с векторной архитектурой (в этом случае он характеризует длину обрабатываемых векторов), и было бы большой ошибкой не считаться с ним при тестировании систем других классов. Дело в том, что практически все современные компьютеры широко используют средства параллельной обработки (конвейеризованная и/или суперскалярная арифметика, MPP-организация системы и т. д.), поэтому оценка производительности при разной глубине программного параллелизма весьма показательна для любой современной системы. Таким образом, в отличие от классического теста Linpack, Linpack в его "кластерном" варианте требует подбора указанных (и ряда других) параметр ов с целью достижения максимальной производительности.

Возвращаясь к истории, следует отметить, что первоначально тест был написан на языке Fortran (и сейчас часто используется эта версия теста), однако для тестирования кластерных систем существует версия на языке C. Основное время теста (свыше 75% времени выполнения) занимает внутренний цикл, выполняющий типичную для действий с матрицами операцию

y(i) = y(i) + a x(i),

представленный тестовой процедурой SAXPY/DAXPY. Поскольку тест LINPACK достаточно хорошо векторизуется и распараллеливается на большинстве систем, имеет смысл компилировать его компиляторами поддерживающими векторизацию.

Как уже говорилось ранее, для тестирования кластерных систем используется версия теста, называемая HPL ( High-Performance Linpack Benchmark, http://www.netlib.org/benchmark/hpl/). В этой версии пользователь имеет возможность задать все значимые параметры алгоритма, подбирая их для достижения наилучшей производительности.

4.2.1.2. Решаемая задача

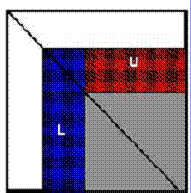
Документация по алгоритму, используемому в Linpack, доступна по адресу http://www.netlib.org/benchmark/hpl/algorithm.html. Как уже упоминалось, тест состоит в решении системы линейных алгебраических уравнений методом LU-факторизации c выбором ведущего элемента столбца.

Рис. 4.1. Схема решения системы линейных уравнений в тесте Linpack

При параллельном процессе на вычислительном кластере исходная матрица разделяется на логические блоки размерностью NB x NB ( NB - параметр алгоритма, задаваемый пользователем, обычно при расчетах лежит в интервале от 32 - 256). Эти блоки в свою очередь разбиваются сеткой P x Q на более мелкие. Каждый из таких блоков "достанется" отдельному процессору системы.

Рис. 4.2. Схема распределения данных при решении системы линейных уравнений в тесте Linpack

Коэффициенты P и Q берутся в зависимости от структуры кластера, а их произведение не может быть больше доступного числа узлов. Если в кластере 8 узлов, то допустимыми значениями P x Q будут: 1x8, 2x4, 3x2, 2x2, 1x4…. При этом в расчетах будут участвовать P x Q процессоров. Именно процессоров, а не узлов (что важно, при использовании в кластере SMP-узлов). Конкретные значения P и Q следует выбирать в зависимости от структуры кластера и коммуникационной среды.

За одну итерацию главного цикла факторизации подвергаются NB столбцов с последующим обновлением оставшейся части матрицы. Результаты разложения пересылаются всем узлам одним из шести алгоритмов распространения (broadcast algorithm):

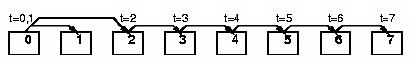
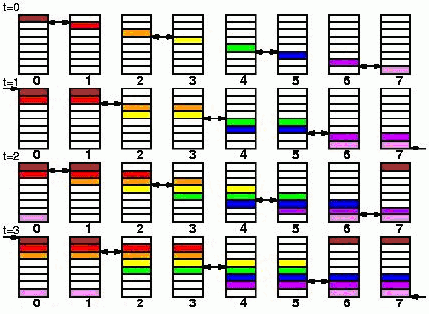
Increasing-ring: Данные пересылаются последовательно 0 -> 1 ; 1 -> 2 ; 2 -> 3 и так далее. Этот алгоритм один из классических:

Increasing-ring (modified): Данные пересылаются в соответствии с правилом 0 -> 1 ; 0 -> 2 ; 2 -> 3 и так далее. Процесс с номером 0 отправляет 2 сообщения и процесс 1 принимает только одно сообщение. Этот алгоритм лучше предыдущего, но не является самым лучшим:

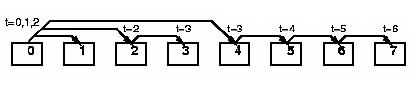
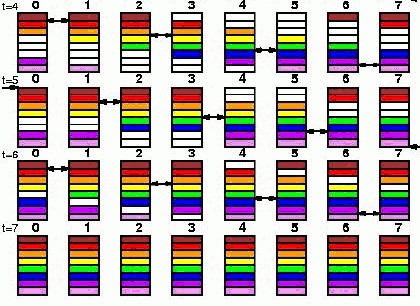
Increasing-2-ring: Q процессов подразделяются на две части: 0 -> 1 и 0 -> Q/2. Далее 1 и Q/2 процессы действуют как источники двух сообщений 1 -> 2, Q/2 -> Q/2+1 ; 2 -> 3, Q/2+1 -> Q/2+2 и так далее:

Increasing-2-ring (modified): Данные пересылаются по схеме: 0 -> 1 ; 0->2 ; 2->3 ( 0->4 ); 2->3 ( 0->4 ) и так далее:

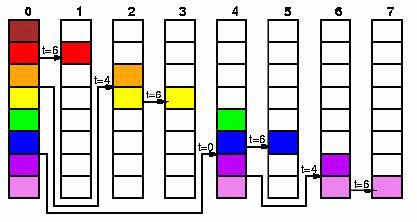
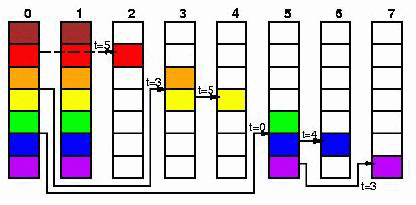
Long (bandwidth reducing): В отличие от предыдущих вариантов, требует синхронизации всех процессов, участвующих в вычислении, для выполнения операции обмена. Передаваемый блок данных разделяется на Q частей, после чего "разбрасывается" по всем процессам, причем обмен разными частями сообщения происходит в разные моменты времени (фаза распределения). После этого, происходят попарные обмены полученными частями сообщений между процессорами (фаза обмена):

Рис. 4.3. Фаза распределения в схеме Long алгоритма рассылки данных

Фаза распределения использует бинарные деревья, фаза обмена- только взаимные обмены сообщениями:

Рис. 4.4. Фаза обмена в схеме Long алгоритма рассылки данных

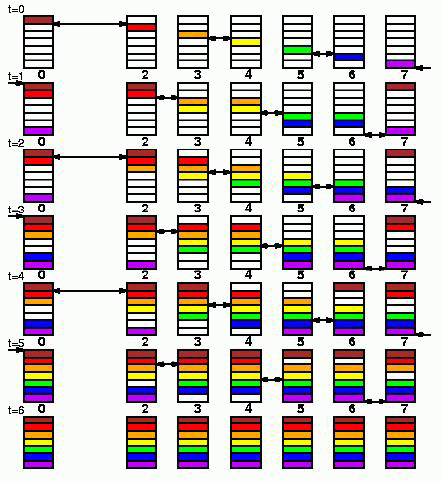
Long (bandwidth reducing modified): похож на выше изложенный вариант, исключая первый шаг от 0 -> 1, затем используется предыдущий Long вариант 0, 2, 3, 4 … Q-1.

Рис. 4.5. Схема обменов данными для алгоритма Long (bandwidth reducing modified)

После того, как разложение закончено, последовательно решается две системы уравнений:

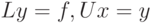
Задача считается успешно решенной, а тест считается выполненным, если выполнены следующие условия:

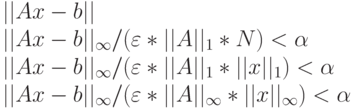
где:

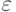• - точность представления чисел с плавающей точкой,
• - константа, задаваемая в конфигурационном файле,
• 
• ,
• ,
• .

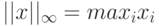4.2.1.3. Использование теста

Для того чтобы воспользоваться тестом необходимо загрузить его дистрибутив (включающий в себя исходный код и makefile-ы, предназначенные для компиляции под различные платформы). Для компиляции также потребуется наличие какой-либо реализации MPI, а также любая реализация библиотеки BLAS (Basic Linear Algebra Subroutines) или библиотеки VSIPL (Vector Signal Image Processing Library).

После сборки получившийся исполняемый модуль использует файл HPL.dat, в котором могут быть указаны существенные параметры алгоритма. Для облегчения проведения тестирования в файле HPL.dat может быть задана последовательность параметров, при этом будет выполнена серия тестов со всеми перечисленными значениями параметров.

Ниже приведен пример конфигурационного файла HPL.dat для теста Linpack, строки которого для удобства пронумерованы

1. HPLinpack benchmark input file
2. Innovative Computing Laboratory, University of Tennessee
3. HPL.out output file name (if any)
4. 0 device out (6=stdout,7=stderr,file)
5. 3 # of problems sizes (N)
6. 1000 2000 3000 Ns
7. 2 # of NBs
8. 112 120 128 NBs
9. 0 PMAP process mapping (0=Row-,1=Column-major)
10. 4 # of process grids (P x Q)
11. 1 2 1 4 Ps
12. 1 2 4 1 Qs
13. 16.0 threshold
14. 1 # of panel fact
15. 0 1 2 PFACTs (0=left, 1=Crout, 2=Right)
16. 2 # of recursive stopping criterium
17. 4 2 NBMINs (>= 1)
18. 1 # of panels in recursion
19. 2 NDIVs
20. 1 # of recursive panel fact.
21. 1 0 2 RFACTs (0=left, 1=Crout, 2=Right)
22. 1 # of broadcast
23. 0 BCASTs (0=1rg,1=1rM,2=2rg,3=2rM,4=Lng,5=LnM)
24. 1 # of lookahead depth
25. 0 DEPTHs (>=0)
26. 2 SWAP (0=bin-exch,1=long,2=mix)
27. 256 swapping threshold
28. 1 L1 in (0=transposed,1=no-transposed) form
29. 1 U in (0=transposed,1=no-transposed) form
30. 0 Equilibration (0=no,1=yes)
31. 8 memory alignment in double (> 0)

В приведенном файле строки 1,2 служат для идентификации файла и более никакой роли не играют (нужно заметить, что они переносятся в файл результата HPL.out). Строки 3,4 определяют, каким образом будет осуществляться вывод результатов теста. Строки 5,6 содержат перечисление размерностей задач, которые будут решаться в ходе теста. Строки 7,8 определяют различные варианты параметра NB. Следует отметить, что тест устроен таким образом, что перебирает всевозможные варианты заданных параметров, таким образом для трех различных размерностей и двух вариантов NB тест будет выполнен шесть раз. Поскольку число различных параметров в конфигурационном файле велико, следует быть осторожным и не забывать об этой особенности. Строки 10,11,12 определяют различные варианты сетки P x Q, для которых будет выполнен тест. Строка 13 задает константу . Остальные строки (14-31) задают другие параметры алгоритма, которые в данном разделе не р ассматривались (обратим лишь внимание на строку 23, задающую один из вариантов алгоритма обмена, о которых речь шла выше)

Результатом работы теста является достаточно объемный файл, в котором для каждого набора параметров, определенном в конфигурационном файле указана достигнутая производительность на тесте, а также имеющаяся погрешность решения.

Ниже приведен фрагмент этого файла (в приведенном примере запуск был осуществлен на одном узле):

====================================================================
HPLinpack 1.0a  --  High-Performance Linpack benchmark  --   January 20, 2004
Written by A. Petitet and R. Clint Whaley,  Innovative Computing Labs.,  UTK
====================================================================

An explanation of the input/output parameters follows:
T/V    : Wall time / encoded variant.
N      : The order of the coefficient matrix A.
NB     : The partitioning blocking factor.
P      : The number of process rows.
Q      : The number of process columns.
Time   : Time in seconds to solve the linear system.
Gflops : Rate of execution for solving the linear system.

The following parameter values will be used:

N      :    1000     2000     3000 
NB     :     112      120 
PMAP   : Row-major process mapping
P      :       1        2        1        4 
Q      :       1        2        4        1 
PFACT  :    Left 
NBMIN  :       4        2 
NDIV   :       2 
RFACT  :   Crout 
BCAST  :   1ring 
DEPTH  :       0 
SWAP   : Mix (threshold = 256)
L1     : no-transposed form
U      : no-transposed form
EQUIL  : no
ALIGN  : 8 double precision words

--------------------------------------------------------------------

- The matrix A is randomly generated for each test.
- The following scaled residual checks will be computed:
   1) ||Ax-b||_oo / ( eps * ||A||_1  * N        )
   2) ||Ax-b||_oo / ( eps * ||A||_1  * ||x||_1  )
   3) ||Ax-b||_oo / ( eps * ||A||_oo * ||x||_oo )
- The relative machine precision (eps) is taken to be         1.110223e-016
- Computational tests pass if scaled residuals are less than           16.0

====================================================================
T/V                N    NB     P     Q      Time             Gflops
--------------------------------------------------------------------
W00C2L4         1000   112     1     1      0.99         6.731e-001
--------------------------------------------------------------------
||Ax-b||_oo /( eps * ||A||_1  * N ) =        1.4543523 ...... PASSED
||Ax-b||_oo /( eps * ||A||_1  * ||x||_1 ) =  0.0352991 ...... PASSED
||Ax-b||_oo /( eps * ||A||_oo * ||x||_oo ) = 0.0085280 ...... PASSED
====================================================================
T/V                N    NB     P     Q      Time             Gflops
--------------------------------------------------------------------
W00C2L2         1000   112     1     1      0.79         8.467e-001
--------------------------------------------------------------------
||Ax-b||_oo /( eps * ||A||_1  * N) =         1.3432175 ...... PASSED
||Ax-b||_oo /( eps * ||A||_1  * ||x||_1 ) =  0.0326017 ...... PASSED
||Ax-b||_oo /( eps * ||A||_oo * ||x||_oo ) = 0.0078763 ...... PASSED
====================================================================