Теорема Робертса
Первое доказательство
Чтобы показать, что функция — это аффинный максимизатор, на самом деле нужно изучать разности. Это потому, что аффинная максимизация на самом деле эквивалентна системе неравенств

где  (рекомендуем читателю не лениться и проверить эту эквивалентность). Мы будем изучать структуру этих самых разностей.
(рекомендуем читателю не лениться и проверить эту эквивалентность). Мы будем изучать структуру этих самых разностей.
Главное множество, которое мы будем изучать, — это
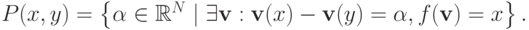
Проще говоря, если 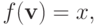 то
то  .
.
В течение доказательства мы увидим, какова структура множеств 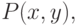 и в конце концов покажем, что
и в конце концов покажем, что 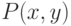 — это полупространство. В частности, мы сделаем два важных замечания о структуре
— это полупространство. В частности, мы сделаем два важных замечания о структуре 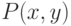 . Во-первых,
. Во-первых,
 |
( 8.1) |
причем внутренности 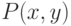 и
и  не пересекаются.
не пересекаются.
А во-вторых, для внутренних точек упомянутых множеств
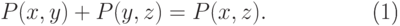 |
( 8.2) |
Для чего нужны эти свойства? Предположим, что  для всех
для всех  (на самом деле это не обязательно так, и нам позже придется сместить множества
(на самом деле это не обязательно так, и нам позже придется сместить множества 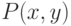 ). Тогда по второму условию все
). Тогда по второму условию все 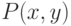 равны. Введем новое обозначение – пусть они равны
равны. Введем новое обозначение – пусть они равны 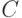 . По первому условию
. По первому условию  : если
: если 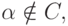 то
то  . Также из первого условия следует, что
. Также из первого условия следует, что 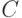 — выпуклое множество: если
— выпуклое множество: если  то
то 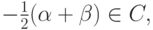 и тогда, используя второе условие, получаем, что
и тогда, используя второе условие, получаем, что 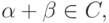 а значит,
а значит, 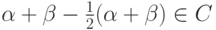 . Противоречие.
. Противоречие.
Таким образом, 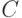 и
и  покрывают все пространство, выпуклы, и их внутренности не пересекаются. Это в точности означает, что они являются подпространствами.
покрывают все пространство, выпуклы, и их внутренности не пересекаются. Это в точности означает, что они являются подпространствами.
Теперь, объяснив идею будущего доказательства, перейдем к нему самому. Начнем с простейших свойств 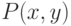 . Так как
. Так как  — сюръекция, то
— сюръекция, то 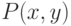 непусто для любых
непусто для любых 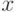 и
и 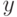 . Также,
. Также,
 |
( 8.3) |
Чтобы это доказать, рассмотрим 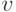 :
: 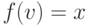 и
и  . Увеличим
. Увеличим 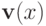 на
на 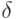 (мы можем это сделать, так как множества типов
(мы можем это сделать, так как множества типов  у нас неограниченные), и получится, что
у нас неограниченные), и получится, что  тоже будет лежать в
тоже будет лежать в 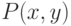 .
.
Следующая лемма докажет нам свойство 8.1 для внутренних точек множества 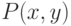 .
.
Лемма 8.4. Рассмотрим произвольные векторы 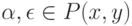 . Тогда
. Тогда

Доказательство. Сначала докажем первую часть леммы. Предположим противное: пусть, наоборот,  . Тогда существует такой вектор типов
. Тогда существует такой вектор типов 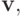 что
что

Но так как  то, значит, существует такой вектор типов
то, значит, существует такой вектор типов 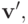 что
что 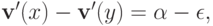 и
и  . Тогда верно, что
. Тогда верно, что
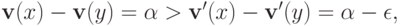
а это противоречит лемме 8.3. Вторая часть леммы доказывается абсолютно аналогично — ее мы оставим читателю.
Пока что мы доказали, что внутренние области 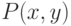 и
и  не пересекаются, и объединение
не пересекаются, и объединение 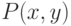 и
и  составляет все пространство.
составляет все пространство.
Отметим еще, что из свойства 8.3 следует, что граница у 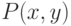 монотонно невозрастающая. Действительно, если граница будет возрастающей, то тогда мы сможем прибавить
монотонно невозрастающая. Действительно, если граница будет возрастающей, то тогда мы сможем прибавить  к
к 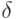 и попасть вне
и попасть вне 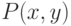 .
.
Осталось только показать, что границы являются гиперплоскостями, и тогда мы докажем все необходимые свойства 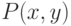 . Также стоит показать, что
. Также стоит показать, что  .
.
Следующая лемма — это доказательство свойства 8.2. В ней понятие "внутренней точки" приобретает исконный смысл, по определению: если  — внутренняя точка, то, значит, для всех достаточно коротких векторов
— внутренняя точка, то, значит, для всех достаточно коротких векторов  верно, что
верно, что  .
.
Лемма 8.5. Рассмотрим некоторые векторы  и некоторые векторы
и некоторые векторы  такие, что
такие, что  . Тогда, если
. Тогда, если
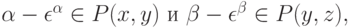
то
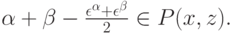
Доказательство. Выберем исход 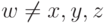 (обратите внимание — мы по делу пользуемся тем, что
(обратите внимание — мы по делу пользуемся тем, что 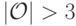 !) и векторы
!) и векторы 
 . Также выберем такой вектор типов
. Также выберем такой вектор типов 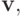 что
что

Значит, они лежат в соответствующих множествах:
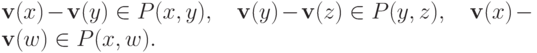
Тогда, по лемме 8.3, 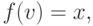 и, следовательно,
и, следовательно,
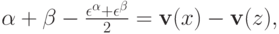
а  несомненно, лежит в
несомненно, лежит в  .
.
Вернемся к доказательству теоремы. Если бы было верно, что 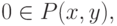 то мы бы уже доказали всю теорему, так как лемма 8.5, примененная к
то мы бы уже доказали всю теорему, так как лемма 8.5, примененная к  доказывала бы, что внутренности всех
доказывала бы, что внутренности всех 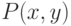 равны. Мы бы доказали, что
равны. Мы бы доказали, что 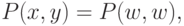 прибавляя к какому-нибудь
прибавляя к какому-нибудь  нулевые векторы. Но нулевой вектор в
нулевые векторы. Но нулевой вектор в 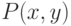 лежать, конечно, не обязан.
лежать, конечно, не обязан.
Чтобы обойти эту досадную трудность, давайте возьмем каждое множество 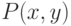 и сдвинем его на
и сдвинем его на

где  — вектор из всех единиц. Число
— вектор из всех единиц. Число  — это нижняя граница множества тех чисел, для которых гиперплоскость
— это нижняя граница множества тех чисел, для которых гиперплоскость 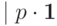 начинает пересекаться с
начинает пересекаться с 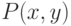 . То есть рассмотрим множество
. То есть рассмотрим множество 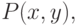 подопрем его гиперплоскостью и начнем эту гиперплоскость понемногу опускать. Когда она наконец-то коснется
подопрем его гиперплоскостью и начнем эту гиперплоскость понемногу опускать. Когда она наконец-то коснется 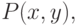 ее коэффициент будет равен
ее коэффициент будет равен  .
.
