Введение в дизайн механизмов
Дизайн механизмов: определения
В этом параграфе мы кратко напомним основные понятия теории игр из прошлой лекции, но приложим их к ситуации дизайна механизмов. Рассмотрим сначала постановку задачи. Что бы мы ни говорили о дизайне, после того самого дизайна начинается собственно игра. В игре участвуют агенты. У игры есть различные исходы. А у каждого агента в этой игре есть некий набор действий, которые он может предпринимать.
Поставим задачу чуть формальнее. Во-первых, введем тип агента 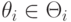 для
для  -го агента (об этом ниже). У игры есть набор исходов
-го агента (об этом ниже). У игры есть набор исходов 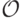 , и для каждого агента каждый исход означает какую-то прибыль (возможно, отрицательную). Так появляется функция полезности (utility function)
, и для каждого агента каждый исход означает какую-то прибыль (возможно, отрицательную). Так появляется функция полезности (utility function)
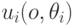
для типа  и исхода
и исхода 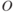 . Агент
. Агент  предпочитает исход
предпочитает исход 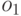 исходу
исходу  , если
, если 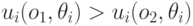 .
.
Стратегия агента — это план, который полностью описывает его поведение во всех возможных состояниях окружающего мира. Через 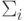 мы будем обозначать множество стратегий агента
мы будем обозначать множество стратегий агента  , через
, через 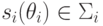 — какую-нибудь конкретную его стратегию. Стратегии бывают чистые и смешанные; чистые стратегии жестко задают поведение в каждом состоянии окружающего мира, смешанные задают распределения вероятностей на множестве возможных действий агента.
— какую-нибудь конкретную его стратегию. Стратегии бывают чистые и смешанные; чистые стратегии жестко задают поведение в каждом состоянии окружающего мира, смешанные задают распределения вероятностей на множестве возможных действий агента.
Например, в аукционе возрастающей цены состояние мира для агента полностью описывается парой 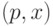 , где
, где  — текущая цена, а бит
— текущая цена, а бит  показывает, является ли агент в текущий момент лидером аукциона. Пусть у агента есть своя (скрытая) оценка лота
показывает, является ли агент в текущий момент лидером аукциона. Пусть у агента есть своя (скрытая) оценка лота 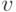 , и он готов заплатить любую сумму, которая была бы меньше
, и он готов заплатить любую сумму, которая была бы меньше 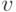 (получив при этом для себя выгоду, равную разности между
(получив при этом для себя выгоду, равную разности между 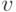 и заплаченной суммой). Тогда так называемая стратегия лучшего ответа (best response strategy)
и заплаченной суммой). Тогда так называемая стратегия лучшего ответа (best response strategy) 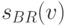 описывается следующим образом:
описывается следующим образом:

Здесь  (от слова bid) — это ставка, которую должен сделать агент. Понятно, что функцию полезности можно с конкретных исходов продолжить на целые стратегии. Если
(от слова bid) — это ставка, которую должен сделать агент. Понятно, что функцию полезности можно с конкретных исходов продолжить на целые стратегии. Если  агентов имеют фиксированные стратегии
агентов имеют фиксированные стратегии 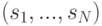 , то функция полезности
, то функция полезности
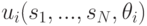
будет просто равна функции полезности 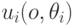 на исходе
на исходе 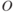 , который однозначно задается этими стратегиями.
, который однозначно задается этими стратегиями.
Рассмотрим тот же аукцион, в котором участвуют два агента и оба исповедуют стратегию лучшего ответа. Для агента 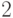 ценность лота
ценность лота 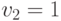 , для агента
, для агента  она равна
она равна  . Тогда функция полезности для первого агента будет равна
. Тогда функция полезности для первого агента будет равна
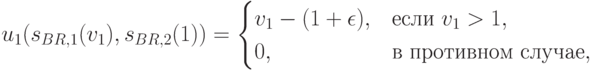
где 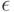 — минимальное увеличение цены в аукционе.
— минимальное увеличение цены в аукционе.
Каждый агент пытается максимизировать свою собственную прибыль. Он решает задачу оптимизации, добиваясь оптимальной стратегии, и в результате система оказывается в каком-нибудь состоянии. Мы будем рассматривать возможные определения равновесного состояния системы, к которому она может прийти после решения каждым агентом своей локальной задачи.
Обозначим через
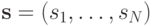
профиль всех стратегий участников. Как и прежде, через
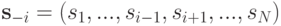
мы будем обозначать стратегии всех участников, кроме  . Введем также аналогичные обозначения
. Введем также аналогичные обозначения  и
и  для типов агентов.
для типов агентов.
Ключевое понятие всей теории игр — равновесие Нэша — мы подробно обсуждали на прошлой лекции. Напомним определение в контексте обозначений теории экономических механизмов.
Определение 2.1. Профиль стратегий 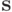 находится в равновесии Нэша, если каждый агент при данных стратегиях других агентов выбирает для себя оптимальную стратегию:
находится в равновесии Нэша, если каждый агент при данных стратегиях других агентов выбирает для себя оптимальную стратегию:
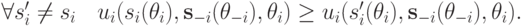
В дилемме заключенного только профиль 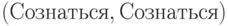 находится в равновесии Нэша — каждому из преступников всегда выгоднее сознаться, чем промолчать. Бывают игры с несколькими равновесиями Нэша.
находится в равновесии Нэша — каждому из преступников всегда выгоднее сознаться, чем промолчать. Бывают игры с несколькими равновесиями Нэша.
Пример 2.1. Приведем пример игры, в которой существуют два равновесия Нэша. Рассмотрим двух игроков, возможные действия каждого из которых — опубликовать один бит. При этом, если биты совпадают, игроки получают по $100, а если не совпадают — платят по $100. Матрица игры выглядит так (доходы игроков совпадают, поэтому мы пишем не пару, а одно значение):
Очевидно, у этой игры два равновесия Нэша: 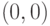 и
и 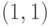 . В каждом из этих состояний ни одному из игроков не выгодно отклоняться от выбранной стратегии.
. В каждом из этих состояний ни одному из игроков не выгодно отклоняться от выбранной стратегии.
Конец примера 2.1.
Равновесие Нэша — фундаментальное понятие, но оно не всегда применимо. Например, оно много чего предполагает о доступной агентам информации. Нужно, чтобы каждый агент знал структуру игры полностью, знал, что другие знают, знал, что все действуют рационально, и, более того, знал, что все выберут одно и то же равновесие Нэша (а их может быть несколько).
На деле агент может и не быть уверен, что все остальные все знают и непременно выберут равновесие Нэша (вообще, редко кто уверен в абсолютной рациональности всех остальных). Но если у агента есть доминантная стратегия, ему все равно.
Определение 2.2. Стратегия 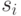 называется доминантной, если она (слабо) максимизирует ожидаемую прибыль агента для всех возможных стратегий других агентов:
называется доминантной, если она (слабо) максимизирует ожидаемую прибыль агента для всех возможных стратегий других агентов:
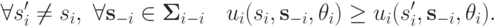
Получается, что в случае, когда у агента есть доминантная стратегия, ему можно вообще ни о чем не беспокоиться: он в любом случае окажется не в проигрыше.
Сейчас мы рассмотрим первый пример нетривиального дизайна механизмов — аукцион Викри (Vickrey auction). Это аукцион, проводящийся по схеме закрытых ставок (sealed-bid): участники подают свои заявки в конвертах, потом их вскрывают, и объект продается тому, кто предложил самую высокую цену. Например, так обычно проводят тендеры.
Что выгодно делать участнику со скрытой ценностью 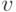 , если ему продадут вещь по той цене, которую он запросит? Это довольно сложная задача: если его скрытая ценность максимальна из всех участников, ему нужно сделать заявку больше, чем у следующего за ним, но желательно только чуть-чуть больше, чтобы максимизировать свою прибыль. Участник, конечно, может решить эту задачу — но ему потребуется масса всяческих предположений, равновесие получится только в ожидании (то есть по Байесу-Нэшу), а не в любом случае (не в доминантных стратегиях), и вообще система будет весьма нестабильной. В результате на самом деле никому не лучше — и продавец не максимизирует доход, и всеобщее благосостояние тоже страдает. Мы потом проанализируем этот случай более подробно.
, если ему продадут вещь по той цене, которую он запросит? Это довольно сложная задача: если его скрытая ценность максимальна из всех участников, ему нужно сделать заявку больше, чем у следующего за ним, но желательно только чуть-чуть больше, чтобы максимизировать свою прибыль. Участник, конечно, может решить эту задачу — но ему потребуется масса всяческих предположений, равновесие получится только в ожидании (то есть по Байесу-Нэшу), а не в любом случае (не в доминантных стратегиях), и вообще система будет весьма нестабильной. В результате на самом деле никому не лучше — и продавец не максимизирует доход, и всеобщее благосостояние тоже страдает. Мы потом проанализируем этот случай более подробно.
Давайте слегка видоизменим аукцион. В новом аукционе (который и называется аукционом Викри) по-прежнему продают тому, кто больше предложил... но продают по цене, которую предложил второй сверху участник! Оказывается, что в таком аукционе участникам выгодно просто говорить правду о своей скрытой ценности, причем это "выгодно" — самое сильное из возможных.
Теорема 2.1. В аукционе Викри правдивая стратегия  является доминантной.
является доминантной.
Доказательство. Ожидаемая полезность стратегии  равна
равна
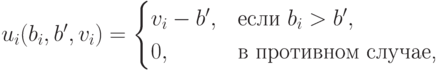
где 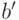 — это наивысшая ставка среди всех остальных агентов. Какие тут могут быть варианты?
— это наивысшая ставка среди всех остальных агентов. Какие тут могут быть варианты?
- Если
 , то оптимальна любая ставка
, то оптимальна любая ставка 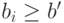 , ведь вещь все равно продадут по цене
, ведь вещь все равно продадут по цене 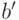 .
. - Если
 , то, опять же, оптимальна любая ставка
, то, опять же, оптимальна любая ставка  (все равно не продадут или продадут с нулевой прибылью).
(все равно не продадут или продадут с нулевой прибылью).
Ставка  подходит для обоих случаев и поэтому является доминантной стратегией. В любом из двух возможных случаев сделать правдивую ставку не хуже, чем любую другую.
подходит для обоих случаев и поэтому является доминантной стратегией. В любом из двух возможных случаев сделать правдивую ставку не хуже, чем любую другую.
Мы только что буквально на пальцах доказали, что в аукционах Викри каждому участнику выгодно сообщать в качестве ставки свою истинную скрытую стоимость. Это очень важное свойство механизмов — правдивость (truthfulness). Позже (в лекции "Принцип выявления предпочтений" ) мы увидим, что на самом деле можно ограничиться только правдивыми механизмами.
Оказывается, что доминантные стратегии гораздо удобнее для агентов: им уже не надо ничего предполагать о других агентах, они могут смело пользоваться доминантной стратегией. Поэтому в дизайне механизмов гораздо приятнее получить механизм с доминантными стратегиями у каждого агента, чем механизм с "обычным" равновесием Нэша.
Но давайте еще раз вернемся к типам агентов; теперь мы предположим, что агент не знает наверняка, каковы типы других агентов, то есть каковы у них функции полезности. Но при этом он знает выплаты для каждого возможного типа, и у него есть некоторое априорное распределение 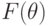 на типах для каждого из других агентов. И, конечно, он пытается максимизировать математическое ожидание своей прибыли в равновесии с такими же оптимизирующими стратегиями других агентов.
на типах для каждого из других агентов. И, конечно, он пытается максимизировать математическое ожидание своей прибыли в равновесии с такими же оптимизирующими стратегиями других агентов.
Определение 2.3. Профиль стратегий 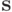 находится в равновесии по Байесу-Нэшу (Bayesian-Nash equilibrium), если каждый агент при известном ему распределении
находится в равновесии по Байесу-Нэшу (Bayesian-Nash equilibrium), если каждый агент при известном ему распределении 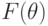 на типах других агентов выбирает для себя оптимальную стратегию:
на типах других агентов выбирает для себя оптимальную стратегию: 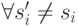

Проще говоря, стратегия агента оптимальна по распределению типов других агентов. В одном конкретном эксперименте вполне возможно, что он будет выбирать неоптимальное поведение, но в среднем при достаточно долгой игре агенту лучше всего выбирать именно эту стратегию.
Равновесие по Байесу-Нэшу обобщает обычное — оно делает более естественные предположения о знаниях агентов. Для каждого фиксированного типа  оно тоже должно быть оптимальным:
оно тоже должно быть оптимальным: 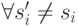
![\mathbf E_{F(\mathbf\theta)}\left[u_i(s_i(\bar\theta_i),\mathbf s_{-i}(\mathbf\theta_{-i}), \theta_i)\mid\bar\theta_i\right] \ge\mathbf E_{F(\mathbf\theta)}\left[u_i(s^\prime_i(\bar\theta_i),\mathbf s_{-i}(\mathbf\theta_{-i}), \theta_i)\mid\bar\theta_i\right].](/sites/default/files/tex_cache/f04efdd1c168bc57b78839513036694c.png)
Но у него есть другие недостатки равновесия Нэша: например, оно в общем случае не единственно. Поэтому хотя равновесие по Байесу-Нэшу получить лучше, чем обычное равновесие Нэша, доминантные стратегии все равно остаются идеальным вариантом.
В итоге мы ввели и рассмотрели три типа равновесий, которые могут возникнуть в наших механизмах. Получается вот такая картинка:
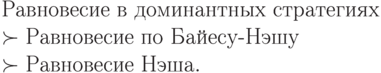
Перейдем теперь собственно к дизайну.
