Возведение в степень
Эффективный алгоритм возведения в целую степень
Представим себе, что нам необходимо возвести число X в целую степень n, полагая, что нам доступна операция умножения. Существует очевидный алгоритм, позволяющий написать собственную реализацию функции Pow.
Работа в классе.
/// <summary>
/// Возведение числа в целую степень
/// </summary>
/// <param name="x">число</param>
/// <param name="n">степень</param>
/// <returns>x в степени n</returns>
static double Pow_Simple(double x, int n)
{
double res = 1;
for (int i = 0; i < n; i++)
res *= x;
return res;
}
А есть ли лучший по сложности алгоритм? Да, такой алгоритм существует. Если наш Simple алгоритм требует n умножений, то эффективный алгоритм требует не более 2 * log n умножений. Нужно понимать, что для больших n логарифм от n значительно меньше n. Например, при n = 220 (n больше миллиона), log n = 20.
Приведу функцию, реализующую эффективный алгоритм. Комментарии позволяют понять идею эффективного алгоритма. Сам по себе алгоритм весьма элегантен. Заодно он демонстрирует способ доказательства корректности алгоритма:
/// <summary>
/// Возведение числа в целую степень
/// эффективный алгоритм
/// </summary>
/// <param name="x">число</param>
/// <param name="n">степень</param>
/// <returns>x в степени n</returns>
static double Pow_Effective(double x, int n)
{
double z = x;
double y = 1;
int m = n;
//выполняется условие (инвариант цикла):
// Invariant: z ^ m * y == x ^ n
while (m != 0)
{
if( m % 2 == 0) //IsEven(m)
{ m /= 2; z *= z; } //инвариант выполняется
else
{ m -= 1; y *= z; }
}
//Invariant && (m == 0) => y == x ^ n
return y;
}
Пример:
n = 33; z = x; y = 1; m = 33; => m = 32; z = x; y = x; => m = 16; z = x ^2; y = x; =>
m = 8; z = x ^ 4; y = x; => m = 4; z = x ^ 8; y = x; => m = 2; z = x ^ 16; y = x; =>
m = 1; z = x ^ 32; y = x; => m = 0; z = x ^ 32; y = x ^ 33; (Всего 6 умножений, а не 33)
Этот алгоритм важен для чисел, но еще в большей степени, когда операции умножения и возведения в степень выполняются для более сложных объектов, чем числа, например, при работе с матрицами или при работе с длинной арифметикой, когда числа могут содержать сотни значащих цифр, что выходит за пределы возможности стандартных типов int и double.
Программа на миллион долларов. Числа "градины" или проблема 3x + 1
Рассмотрим короткую программу в несколько строчек:
/// <summary>
/// Знаменитая программа
/// Пока никому не удалось доказать ее завершаемость
/// для любого целого n
/// Объявлена награда в миллион долларов
/// </summary>
/// <param name="n">целое</param>
/// <returns>число проходов по циклу</returns>
static int Grad(long n)
{
int res = 0;
while (n != 1)
{
if (n % 2 == 0) //IsEven(n)
n /= 2;
else
n = 3 * n + 1;
res++;
}
return res;
}
Доказано, что программа завершается для любых nN, где N – большое число. Но пока никому не удалось доказать ее завершаемость для любого n.
Можно написать программу, проверяющую завершаемость для всех n из заданного интервала. Приведу программу, которая находит максимальную "градину" - число, у которого число колебаний максимально:
/// <summary>
/// Наибольшая "градина"
/// в интервале [3, N]
/// </summary>
/// <param name="N">верхняя граница</param>
/// <param name="Max">наибольшая градина в интервале</param>
/// <param name="K_max">число колебаний градины</param>
public static void MaxGrad(int N, out int Max, out int K_max )
{
K_max = 0;
int n;
Max = 0;
for (int i = 3; i < N; i += 2 )
{
n = Grad(i);
if (n > K_max)
{
K_max = n;
Max = i;
}
}
}
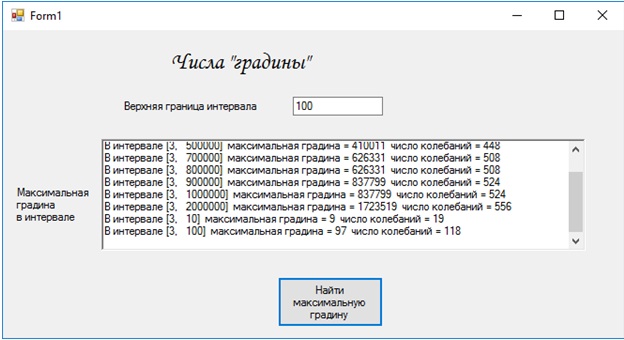
Приведу интерфейс проекта, анализирующего поведение чисел "градин":
Этой замечательной программой мы завершим эту часть нашего курса.
Итоги
На заключительном занятии практически все школьники представили свой вариант игры "Однорукий бандит", что свидетельствует о том, что основами программирования они овладели. Все они продолжили обучение в следующем учебном году. В трейлере, подготовленном для этого курса, можно услышать, как школьники оценивают прослушанный ими курс.