Делители числа
13 классических задач
- (**) Перевод числа N из системы с основанием p в систему с основанием q.
- (*) Расщепление числа N на цифры.
- (*) Является ли число палиндромом?
- () Является ли число четным?
- () Является ли число d делителем числа N?
- (**) Нахождение делителей числа N.
- () Является ли число простым?
- (**) Нахождение простых чисел.
- () Является ли число совершенным?
- (*) Нахождение совершенных чисел.
- (*) Наибольший общий делитель и наименьшее общее кратное чисел N и M.
- (**) Возведение в целую степень.
- (*…*) Числа "градины". Проблема "3*N + 1"
Задача 1. Перевод целых чисел из системы счисления с основанием p в систему счисления с основанием q
Эту задачу мы уже рассматривали. Повторение – мать учения.
Для любой позиционной системы счисления справедливо следующее утверждение:
Целое число N в системе счисления с основанием p представимо в виде:
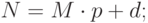 |
( 7.1) |
Здесь d – цифра системы p – младшая цифра записи числа N в системе p,
M – целое число, полученное обрезанием младшей цифры числа N.
Операции % и / позволяют получить d и M.
Выполняя эти операции в цикле, пока число не станет равным нулю, можно перевести число N в систему с основанием p.
Вот соответствующая знакомая нам функция:
/// <summary>
/// Перевод целого положительного десятичного числа
/// в систему с основанием p
/// </summary>
/// <param name="N">десятичное число</param>
/// <param name = "p">основание системы счисления</param>
/// <returns>число N в системе p, представленное как строка текста</returns>
public static string From10ToP(int N, int p)
{
string res = ""; //результат перевода
int digit; //текущая цифра числа в системе p
while( N != 0)
{
digit = N % p; //получаем последнюю цифру
N = N / p; //отрезаем последнюю цифру
res = digit.ToString() + res; //присоединяем цифру слева к результату
}
return res; //возвращаем результат
}
Работа у доски
Также просто решается обратная задача – перевод числа из системы p в десятичную систему. Если дано целое число M и к нему нужно присоединить справа следующую цифру d, то можно непосредственно воспользоваться соотношением (7.1), умножая M на p и прибавляя цифру d.
Выполняя эти операции в цикле по числу цифр числа, можно перевести число из системы p в десятичную систему.
Вот знакомая нам функция перевода:
/// <summary>
/// перевод целого положительного числа из системы с основанием p
/// в десятичное число
/// </summary>
/// <param name="N">число N в системе p, представленное как строка текста</param>
/// <param name="p">основание системы счисления</param>
/// <returns>десятичное число</returns>
public static int FromPTo10(string N, int p)
{
int res = 0; //результат перевода
int digit; //текущая цифра
int n = N.Length; //длина строки - число цифр в записи N
for (int i = 0; i < n; i++) //цикл по числу цифр, начиная со старшей цифры
{
digit = N[i] - '0'; //цифра как разность кода цифры и кода цифры 0
res = res * p + digit; //присоединяем цифру к результату
}
return res; //возвращаем результат
}
Работа у доски
Для перевода числа N из системы p в систему q можно вначале перевести N из p в десятичную систему, а затем выполнить перевод из десятичной системы в систему q.
Вот соответствующая функция:
/// <summary>
/// перевод целого положительного числа из системы с основанием p
/// в систему с основанием q
/// </summary>
/// <param name="N">число N в системе p, представленное как строка текста</param>
/// <param name="p">основание исходной системы счисления</param>
/// <param name="q">основание результирующей системы счисления</param>
/// <returns>число N в системе q, представленное как строка текста</returns>
public static string FromPToQ(string N, int p, int q)
{
int NN = FromPTo10(N, p);
return From10ToP(NN, q);
// return From10ToP(FromPTo10(N, p), q); //короткая запись - вызов в вызове
}
Работа у доски
