НОУ ИНТУИТ | Квантовые вычисления. Лекция 17: Быстрое преобразование Фурье

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.06.2019 | Доступ: свободный | Студентов: 511 / 78 | Длительность: 09:11:00

Темы: Программирование, Математика, Физика, Суперкомпьютерные технологии

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

В качестве упражнения следует вывести формулу для коэффициента 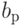b_р .

$b_p=\frac{b_p^g+b_p^h}{\sqrt2}\cos\left(\frac{(2p+1)\pi}{2^{n+1}}\right)+\frac{-a_p^g+a_p^h}{\sqrt2}\sin\left(\frac{(2p+1)\pi}{2^{n+1}}\right)$

Помните, что БПФ - рекурсивный алгоритм, так что коэффициенты последовательностей g и h снова считаются рекурсивно, расщепляя каждую из них на короткие последовательности. Формулы исходного преобразования Фурье применяются только, когда приходим к последовательностям длины 2: 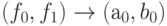$(f_0, f_1)\to (а_0, b_0)$ :

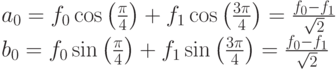
$a_0=f_0\cos\left(\frac{\pi}{4}\right)+f_1\cos\left(\frac{3\pi}{4}\right)=\frac{f_0-f_1}{\sqrt2}\\ b_0=f_0\sin\left(\frac{\pi}{4}\right)+f_1\sin\left(\frac{3\pi}{4}\right)=\frac{f_0-f_1}{\sqrt2}$

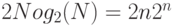Теорема. Сложность алгоритма БПФ для вектора длины N = 2^n г равна $2N \1og_2(N) = 2n2^n$ .

Доказательство. Докажем теорему индукцией по n. Для базиса индукции, n = 1, N = 2, где используются простые формулы, приведенные выше, число умножений равно 2, что лучше, чем 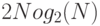$2N \1og_2(N)$ .

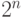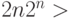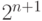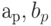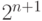Давайте рассмотрим шаг индукции. Наше индукционное предположение - для последовательности длины 2^n сложность БПФ равна 2n2^n> . Оценим сложность БПФ для последовательности длины $2^{n+1}$ . Чтобы вычислить коэффициенты Фурье а_р, b_p мы вначале выполняем БПФ для последовательностей g и h со сложностью 2 * 2n2^n . Тогда для вычисления каждого из $2^{n+1}$ коэффициентов Фурье необходимо выполнить два умножения. Общая сложность тогда:

$2*2n2^n+2*2^{n+1}=2(n+1)2^{n+1}$

Тем самым теорема доказана.

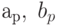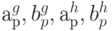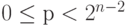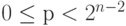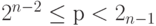Остается одно важное замечание. Когда мы выражаем коэффициенты Фурье $а_р,\; b_p$ через а_р^g, b_p^g, а_р^h, b_p^h , индекс р находится в пределах $0 \le р <2^{n-2}$ . Однако, коэффициенты Фурье для g и h определены только для индексов в пределах $0 \le р < 2^{n-2}$ . Следующая теорема объясняет, как получить коэффициенты Фурье для g и h в пределах $2^{n-2} \le р < 2_{n-1}$ .

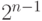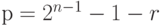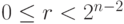Теорема. Пусть g - вектор длины $2^{n-1}$ . Пусть $р = 2^{n-1} - 1 - r$ , где $0 \le r < 2^{n-2}$ . Тогда

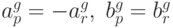
$a_p^g=-a_r^g,\; b_p^g=b_r^g$

Аналогичное отношение имеет место и для коэффициентов Фурье для h.

Доказательство. Напомним, что коэффициенты Фурье а_р^g задаются формулой:

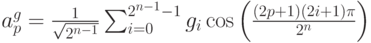
$a_p^g=\frac{1}{\sqrt{2^{n-1}}}\sum_{i=0}^{2^{n-1}-1}g_i\cos\left(\frac{(2p+1)(2i+1)\pi}{2^n}\right)$

Подставляя 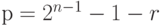$р = 2^{n-1} - 1 - r$ , получим

$a_p^h=\frac{1}{\sqrt{2^{n-2}}}\sum_{i=0}^{2^{n-1}-1}g_i\cos \left( \frac{(2^n-2r-1)(2i+1)\pi}{2^n}\right) =\frac{1}{\sqrt{2^{n-1}}}\sum_{i=0}^{2^{n-1}-1}g_i\cos\left((2i+1)\pi-\frac{(2r+1)(2i+1)\pi}{2^n}\right)$

Используя тождества 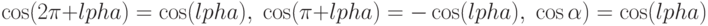$\cos(2\pi + \аlpha) = \cos(\аlpha),\; \cos(\pi + \аlpha) = - \cos(\аlpha),\;\cos{\alpha) = \cos(\аlpha)$ , упростим формулу и получим:

$a_p^g=-\frac{1}{\sqrt{2^{n-2}}}\sum_{i=0}^{2^{n-1}-1}g_i\cos\left(\frac{(2r+1)(2i+1)\pi}{2^n}\right)=-a_r^g$

Доказательство для 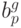b_p^g остается в качестве упражнения.

В случае, когда 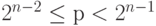$2^{n-2} \le р < 2^{n-1}$ , запишем р как 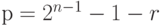$р = 2^{n-1} - 1 - r$ и мы можем вычислить коэффициенты Фурье для f из коэффициентов Фурье для g и h следующим образом:

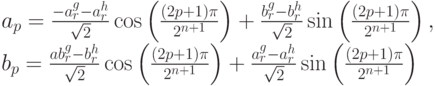
$a_p=\frac{-a_r^g-a_r^h}{\sqrt2}\cos\left(\frac{(2p+1)\pi}{2^{n+1}}\right) +\frac{b_r^g-b_r^h}{\sqrt2}\sin\left(\frac{(2p+1)\pi}{2^{n+1}}\right),\\ b_p=\frac{ab_r^g-b_r^h}{\sqrt2}\cos\left(\frac{(2p+1)\pi}{2^{n+1}}\right) +\frac{a_r^g-a_r^h}{\sqrt2}\sin\left(\frac{(2p+1)\pi}{2^{n+1}}\right)$

Давайте выразим тригонометрические множители в правой части в терминах r:

$\cos\left(\frac{(2p+1)\pi}{2^{n+1}}\right)=\cos\left(\frac{(2^n-2r-1)\pi}{2^{n+1}}\right)=\cos\left(\frac{\pi}{2}-\frac{(2r+1)\pi}{2^{n+1}}\right)=\sin\left(\frac{(2r+1)\pi}{2^{n+1}}\right)$

На последнем шаге мы использовали тождество 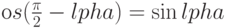$\соs(\frac{\pi}{2} - \аlpha) = \sin \аlpha$ . Аналогично:

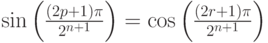
$\sin\left(\frac{(2p+1)\pi}{2^{n+1}}\right)=\cos\left(\frac{(2r+1)\pi}{2^{n+1}}\right)$

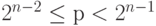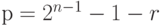Теперь для $2^{n-2} \le р < 2^{n-1}$ , где $р = 2^{n-1} - 1 - r$ , получим:

$a_p=\frac{-a_r^g-a_r^h}{\sqrt2}\sin\left(\frac{(2r+1)\pi}{2^{n+1}}\right)+\frac{b_r^g-b_r^h}{\sqrt2}\cos\left(\frac{(2r+1)\pi}{2^{n+1}}\right),\\ b_p=\frac{b_r^g+b_r^h}{\sqrt2}\sin\left(\frac{(2r+1)\pi}{2^{n+1}}\right)+\frac{a_r^g-a_r^h}{\sqrt2}\cos\left(\frac{(2r+1)\pi}{2^{n+1}}\right)$

Дальше >>

Авторизоваться

Квантовые вычисления

Быстрое преобразование Фурье

Вопросы и ответы