Ортогональные линейные трансформации

1. Т - ортогональная трансформация;
2. Т - сохраняет скалярное произведение;
3. Т - сохраняет длины и углы;
4. Т - сохраняет длины векторов.

В выше приведенном обсуждении мы доказали, что .

В классе линейных трансформаций существует трансформация со свойствами, подобными числовой единице. Тождественная трансформация I, действующая в векторном пространстве V - это трансформация, не изменяющая ни один из векторов: I(v) = v для всех векторов v.

Рассмотрим тождественную трансформацию в 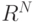. Так как 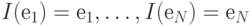, то матрица тождествеиной трансформации является диагональной матрицей с единицами по диагонали и нулями для остальных элементов (матрицу тождественной трансформации называют единичной матрицей по аналогии с единицей). Эту матрицу также будем обозначать как I:

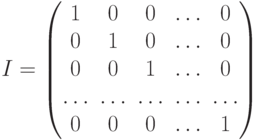
Тождественная трансформация I имеет очевидные свойства относительно композиции трансформаций: 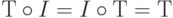для всех трансформаций Т векторного пространства V. Как следствие, те же свойства справедливы для единичной матрицы I относительно умножения матриц: АI = IА = А.

Линейные трансформации можно обобщить, задав для них свойство, подобное инверсии чисел.

1Операция деления вещественных чисел позволяет ввести понятие обратного числа. Число b = 1/а называется числом, обратным к числу а, или инверсией числа а. Очевидны равенства аb = bа = 1. Все вещественные числа за исключением числа 0, имеют обратные числа.

Определение. Линейная трансформация S называется инверсией (обращением) Т (обозначается 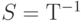), если 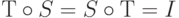. Аналогично для матриц: 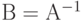,если АВ=ВА=I.

Упражнение. Проверьте что

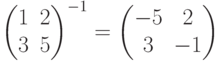
Для вещественных чисел 0- единственное число, не имеющее обратного числа. для матриц существуют ненулевые матрицы, не имеющие обратных матриц.

Упражнение. Покажите, что матрица

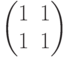
не имеет обратной матрицы.

Приведем без доказательства следующее утверждение относительно квадратных матриц размера N * N. Если АВ = I, то ВА = I. Из этого следует, что подобное утверждение справедливо для линейных трансформаций в 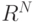: Если 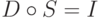, но .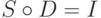

Упражнение. Покажите, что выше приведенное утверждение не вьшолняется для линейных трансформаций в бесконечномерном векторном пространстве. Пусть D, S - линейные трансформации в пространстве полиномов, такие что и 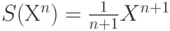. Покажите, что , но .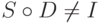

Определение. Транспонированной матрицей А (обозначается 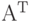) называется матрица, у которой строка с индексом k, является столбцом матрицы А с тем же индексом k.

Вот пример транспонирования матрицы:

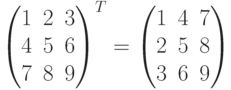
Теорема. Каждая ортогональная матрица обратима. Обратная матрица совпадает с транспонированной матрицей: .

Доказательство. Нам нужно показать, что 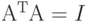. Поскольку 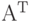-транспонированная матрица, то элемент с индексами j, k матрицы произведения представляет скалярное произведение j-го и k-го столбцов. Для диагональных элементов, когда j = k, это произведение равно единице - длине вектора, в остальных случаях ввиду ортогональности векторов оно равно нулю. Отсюда следует, что матрица произведения является единичной матрицей - матрицей I- матрицей тождественной трансформации.