Простые проценты
2.9 Эквивалентность учетной и процентной ставок
Продолжим обсуждение формулы, которую банк использует при учёте векселя:
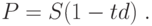
Для банка, учитывающего вексель на сумму S, учётная стоимость векселя P является приведенной стоимостью суммы S, которую банк получит от векселедателя при погашении векселя. Погашение векселя произойдет через срок t. При обычном инвестировании ситуация противоположная: известна начальная сумма P, на которую начисляется процент r, а конечная сумма S вычисляется по формуле

Предположим, что t=1, то есть рассматривается период, равный одному году. Тогда имеем следующие формулы для процентных ставок начисления и учёта:
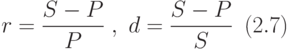
Преобразуем формулы (2.7) к виду:

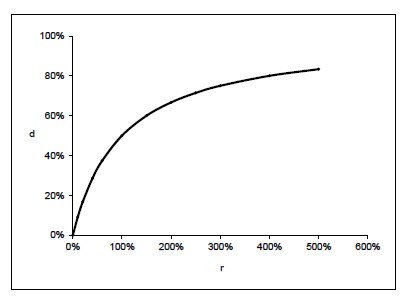
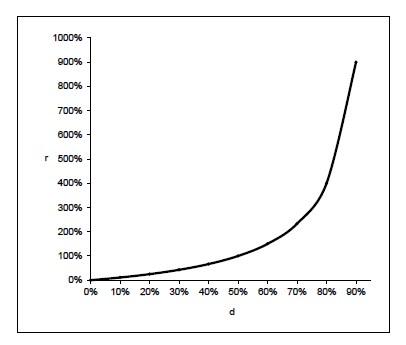
Из формул (2.8) получаем формулы, связывающие значения r и d (за один год), которые часто называют условиями эквивалентности учётной и процентной ставок:
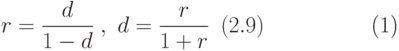
Графическое изображение зависимостей, выраженных формулами (2.9), приведено на рис. 3 и рис. 4.
Из формул (2.9) следует ещё одна интерпретация процента учета d. Пусть сумма S=1 хранится 1 год на депозите при процентной ставке r. В конце года сумма процентов на S будет равна r. Приведенное значение суммы процентов r будет равно

Следовательно, можно считать, что дисконт d является суммой процентов, которые выплачиваются не в конце, а в начале периода.
Таким образом, различие между процентной и учетной ставками в том, что они оценивают один и тот же поток платежей относительно разных моментов времени. Для процентной ставки это начало периода, для учетной - конец периода. Рассмотрим пример.
Пример 31. Вычислим приведённую стоимость 10 000 руб., получаемых через год: а) при процентной ставке 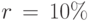 ; б)при учетной ставке
; б)при учетной ставке 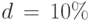 .
.
Решение. При процентной ставке 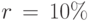 получаем:
получаем:
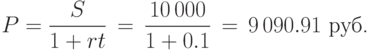
При при учетной ставке 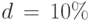 получаем:
получаем:
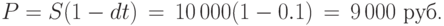
Необходимо помнить, что эквивалентность процентной и учетной ставок устанавливается только для определенного периода времени t. Формулы (16) получены при 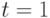 . В общем случае они принимают вид:
. В общем случае они принимают вид:

2.10 Влияние инфляции на ставку процента
Интересно рассмотреть одновременное влияние процессов дисконтирования по ставке r и инфляции по ставке i за один период. Инфляция, определяемая на микроэкономическом уровне как общий уровень роста цен типичной потребительской корзины (CPI - Consumer Price Index), означает, что на сегодняшние деньги вы сможете купить в 1+i раз меньше товара в конце периода. В результате современная сумма P эквивалентна по покупательной способности сумме S, определяемой формулой:

В этих обстоятельствах величину наращенного процента можно рассчитывать как в реальных деньгах - номинальный процент, так и по покупательной способности (с поправкой на инфляцию) - реальный процент.
Ясно, что при наличии инфляции ставка номинального процента больше ставки реального процента. Номинальный процент должен использоваться в вычислениях в реальных терминах (без поправки на инфляцию). Реальный процент используется, если данные специальным образом очищены от влияния инфляции.
Пусть сначала r - номинальный процент. Тогда после дисконтирования получаем:
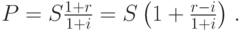
Если величина инфляции невелика, то 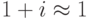 , откуда верна следующая приближенная формула:
, откуда верна следующая приближенная формула:

Следует заметить, что в условиях, характерных для России последнего десятилетия XX века, когда величина i менялась порой от тысяч до многих десятков процентов в год, пользоваться последней формулой было нельзя.
При переходе к рассмотрению реального процента 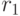 следует учесть, что величина инфляции - ожидаемая величина, поэтому величина
следует учесть, что величина инфляции - ожидаемая величина, поэтому величина 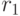 не может определяться нормативно - она получается в результате построения модели поведения инвестора. Простейшая модель Фишера утверждает, что номинальный процент r связан с реальным процентом
не может определяться нормативно - она получается в результате построения модели поведения инвестора. Простейшая модель Фишера утверждает, что номинальный процент r связан с реальным процентом 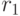 с помощью формулы:
с помощью формулы:

Согласно этой модели, норма процента полностью встроена в ценовой механизм. Номинальный процент включает в себя инфляционную премию, достаточную для того, чтобы кредитор получил компенсацию за уменьшенную покупательную способность будущих денег. Важно подчеркнуть, что номинальный процент строится на прогнозе, а не на историческом анализе инфляции за прошедший период. Фактические величины инфляции за предыдущий период играют роль для оценки инфляции на следующий период, но вовсе не основную.
Имеются и более сложные модели, учитывающие, например, разницу в ставках налогообложения - в этом случае разные группы инвесторов будут описываться различными моделями.
При высокой инфляции и отсутствии на рынке инструментов с достаточной номинальной доходностью получаем ситуацию с отрицательной реальной нормой процента, имевшую место в России, например, в 1993 г. (см. дискуссию в журнале "Экономика и математические методы" за 1994 г.). Рассмотрим два простых численных примера.
Пример 32. В начале 1996 г. ожидаемая годовая инфляция в России находилась на уровне 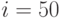 . Годовой сертификат Сбербанка на сумму 1 млн. руб. давал номинальную доходность
. Годовой сертификат Сбербанка на сумму 1 млн. руб. давал номинальную доходность 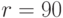 (это то, что было прямо написано на сертификате). Посчитаем реальную доходность сертификата.
(это то, что было прямо написано на сертификате). Посчитаем реальную доходность сертификата.
Решение. Для вычисления реального процента применим формулу (2.12):
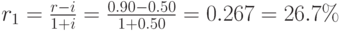
Заметим, что для реального процента в надежном банке это очень много, что означает встроенность в предлагаемый процент рисковой премии.
Пример 33. В рассматриваемый год ожидаемая инфляция составляет 20%. Определим, какую номинальную годовую процентную ставку следует установить по вкладам в банке, чтобы реальная годовая ставка 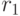 равнялась 5%.
равнялась 5%.
Решение. Значение номинальной годовой процентной ставки найдем из формулы (2.12):
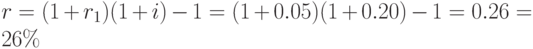
Список ключевых терминов
Вексель - ценная бумага, являющаяся простейшим типом долгового обязательства.
Дисконт - процентный доход, вычитаемый из ссуды в момент её выдачи.
Инфляция - снижение покупательной способности денег.
Номинальная ставка процента - ставка процента, зафиксированная в финансовом договоре.
Приведённая ценность - ценность потока платежей в определённый момент времени с учётом дисконтирования.
Простой процент - схема начисления процентов, при которой базой в течении всего рассматриваемого периода является исходная сумма.
Процентный пункт - единица, применяемая для сравнения величин, выраженных в процентах.
Реальная ставка процента - процентная ставка с учётом инфляции.
Учёт векселя - покупка банком или специализированными кредитными учреждениями векселя до наступления срока его оплаты.
Учётная ставка - процентная ставка, применяемая при учёте векселя.
Эквивалентные контракты - контракты, имеющие равные приведённые ценности потоков платежей по этим контрактам.
Краткие итоги
В лекции рассмотрено применение простого процента в задачах оценивания следующих финансовых объектов и операций с ними: банковский депозит, вексель, финансовый контракт.