Нейроподобные модели как формально-логический базис анализа живых систем
8.2. Многопороговая модель биологического кода
Проведенный в предыдущем разделе анализ проблем инструктированного синтеза "надежных" гетероструктур из "ненадежных" компонент показал, что безусловными "лидерами" в освоении таких технологий являются молекулярно-биологические системы. Поэтому для промышленного освоения нано- и супрамолекулярных технологий имеет смысл воспроизвести в технике методы и средства синтеза сложных молекулярно-биологических комплексов.
Термин "структурная информация" широко использовался в научно-технической литературе 60-х годов прошлого столетия, чтобы подчеркнуть факт наличия в природе информации, для измерения количественных характеристик которой нет необходимости привлекать вероятностные или статистические методы оценки по Винеру - Шеннону [54]. Этим термином обычно характеризуют начальную упорядоченность или организованность кибернетических, биологических и т. п. систем.
В вычислительной технике под информацией понимаются коды инструкций и данных, которые однозначно связаны со значениями тех или иных физических параметров электромагнитных, оптических, акустических и т. п. сигналов. Поэтому формально-логическая обработка такой информации на физическом уровне сводится к преобразованию значений параметров входных сигналов в значения параметров выходных сигналов, которые могут не совпадать по физической модальности.
Напротив, в живых системах рост, развитие и размножение организмов, а также их эволюционное становление неразрывно связаны со структурными и параметрическими методами и средствами кодирования и преобразования информации. Все перечисленные процессы реализуются через взаимодействие субъединиц таких систем, вследствие чего их структура постоянно меняется, и поэтому в задачах анализа и синтеза организмов невозможно абстрагироваться от того факта, что в материальном мире нет и не может быть взаимно однозначного соответствия между структурой и функцией.
Последнее обстоятельство играет решающую роль в формировании механизмов конвергентного замыкания условных рефлексов [25], когда
требуется установить устойчивую причинно-следственную связь между пока еще индифферентным возбуждением и последующей реакцией, обеспечивающей организму полезный приспособительный эффект. Такое замыкание осуществляется на уровне метаболических процессов конвергентных нейронов, где только и возможно взвешенное сопоставление оперативного опыта "(само)обучающейся" особи с опытом ее эволюционного становления и развития. Отсюда: в "сложных" живых системах иерархического типа широко используются механизмы трансформации межнейрональных взаимодействий на уровень многостадийных метаболических процессов конвергентных нейронов, где действуют законы квантовой механики [216]. Согласно [34], эти механизмы должны прямо или опосредовано влиять на процедуры инструктированного синтеза полимеров нативного белка, которые невозможны без участия биологического кода.
Нейроподобные методы и средства (пере)распределения и трансформации задач, решаемых на разных уровнях иерархии, приобретают особую актуальность для супрамолекулярной и наноэлектроники [36, 186], где высокий структурно-функциональный полиморфизм зависит от множества плохо контролируемых внешних воздействующих факторов [94]. В таких условиях снизить требования к времени устойчивой реализации заданной арифметико-логической функции можно за счет высокодинамичной (ре) генерации, а значит, и высокодинамичного инструктированного синтеза нанометровых или супрамолекулярных вычислительных гетероструктур PD -ассоциативного типа [232], в которых один из преобразуемых операндов управляет синтезом "рабочего тела" вычислителя и запоминается в его структуре на все "время жизни", а выполняемая функция зависит как от структуры вычислителя, так и от содержимого второго, потокового операнда. Поэтому в PD -ассоциативных технологиях, как и в молекулярной биологии, процессы производства и использования вычислителей совмещаются во времени и пространстве. При этом удается отказаться от формирования исполняемых инструкций на основе трудоемких этапов формализации задач, их алгоритмизации и программирования, если сами вычисления проводить на ней-роподобной элементной базе [87], работу которой описывают с помощью традиционных моделей формальных нейронов [64, 71]. Математическую основу таких моделей составляет аппарат пороговой логики [77].
Отсюда и встает задача разработки единых для молекулярной биологии и супрамолекулярной вычислительной техники формальных методов и средств неоднозначной трансформации формы представления информации из параметров сигнала в структурно-функциональную схему синтезируемой гетероструктуры (кодирование) и, наоборот, извлечения информации в виде отклика этой гетероструктуры на слабое, неразрушающее идентификационное воздействие (декодирование).
Предлагаемая формальная модель молекулярно-биологического кода основана [230]:
- на таблице вырожденности реального биологического кода (табл. 8.1), в которой триплеты УАА, УАГ и УГА отнесены к подмножеству кодонов, которые обеспечивают терминацию (завершение) синтеза полимеров белка.
- на экспериментальном факте: при взаимной идентификации антикодонов транспортной рибонуклеиновой кислоты (
 -РНК) и инициализированных рибосомой кодонов информационной РНК (
-РНК) и инициализированных рибосомой кодонов информационной РНК (  -РНК) "вклад" (
-РНК) "вклад" ( 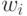 ) нуклеотида определяется его положением в триплете:
) нуклеотида определяется его положением в триплете:  Здесь индексы
Здесь индексы 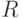 ,
,  и
и 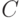 соответствуют правому, левому и центральному положению основания в триплете, а состав кодонов и антикодонов определяется по правилу комплементарного спаривания оснований: "аденин (А) - урацил (У)" и "гуанин (Г) - цитозин (Ц)".
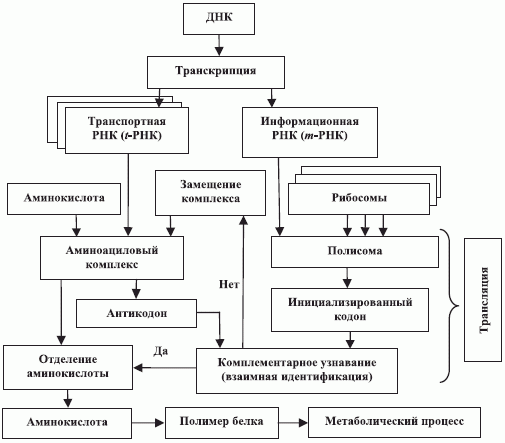
соответствуют правому, левому и центральному положению основания в триплете, а состав кодонов и антикодонов определяется по правилу комплементарного спаривания оснований: "аденин (А) - урацил (У)" и "гуанин (Г) - цитозин (Ц)". - на многофазной модели структурного синтеза полимеров натив-ного белка (рис. 8.1), который осуществляется через структурно-параметрическое узнавание кодонов
 -РНК комплементарными антикодонами
-РНК комплементарными антикодонами  -РНК, которые "нагружены" аминокислотами, включаемыми в состав нативного белка (рис. 8.2 [233]). При этом предполагается как достаточное количество всех исходных компонентов (нуклеотидов, ферментов, аминокислот и т. п.), участвующих в синтезе, так и выполнение требуемых условий их взаимодействия (температура, парциальное давление, вязкость и так далее).
Это позволяет абстрагироваться от физико-химических закономерностей синтеза и использовать для его описания формальные методы, которые отражают только вариативный характер процедур взаимного узнавания кодонов и антикодонов.
-РНК, которые "нагружены" аминокислотами, включаемыми в состав нативного белка (рис. 8.2 [233]). При этом предполагается как достаточное количество всех исходных компонентов (нуклеотидов, ферментов, аминокислот и т. п.), участвующих в синтезе, так и выполнение требуемых условий их взаимодействия (температура, парциальное давление, вязкость и так далее).
Это позволяет абстрагироваться от физико-химических закономерностей синтеза и использовать для его описания формальные методы, которые отражают только вариативный характер процедур взаимного узнавания кодонов и антикодонов.
Введем следующие формальные определения и соглашения, которые не лишены молекулярно-биологического смысла:
- Под идентификационной активностью некоторой элементарной молекулярно-биологической структуры (нуклеотидов ДНК и РНК, а также аминокислот) будем понимать однозначно измеренный отклик этой структуры на слабое, не разрушающее входное воздействие произвольной биологической, биохимической или биофизической модальности.
Идентификационную активность нуклеотидов, участвующих в синтезе полимеров нативного белка, обозначим
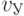 ,
, 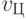 ,
, 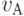 и
и 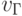 . Тогда идентификационную активность (анти)кодонов
. Тогда идентификационную активность (анти)кодонов 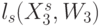 можно оценить взвешенной суммой идентификационных активностей составляющих нуклеотидов:
можно оценить взвешенной суммой идентификационных активностей составляющих нуклеотидов: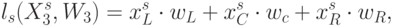
( 8.1) где входной вектор
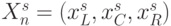 пробегает (по
пробегает (по  ) все комбинации значений идентификационной активности нуклеотидов
) все комбинации значений идентификационной активности нуклеотидов  ;
;  ;
;  ; компоненты "весового" вектора
; компоненты "весового" вектора 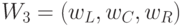 отражают реальный вклад каждого нуклеотида в процедуру идентификации триплета, а
отражают реальный вклад каждого нуклеотида в процедуру идентификации триплета, а 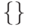 - символ множества.
- символ множества. - Из 24 возможных способов упорядочения уровней идентификационной активности нуклеотидов зафиксируем один:
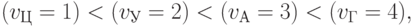
( 8.2) а отображение "множество активностей нуклеотидных триплетов - множество активностей аминокислот" ограничим классом дискретных функций вида:
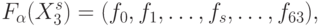
( 8.3) где идентификационная активность аминокислот
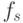 пробегает все множество целочисленных значений
пробегает все множество целочисленных значений 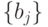 с учетом одного "пустого" мономера, отвечающего кодонам терминации, то есть
с учетом одного "пустого" мономера, отвечающего кодонам терминации, то есть 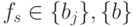 - это
- это  и так далее до
и так далее до  ;
; 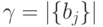 ;
;  , а
, а 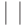 - мощность множества. Наличие в спектре значений дискретной функции (8.3) "пустого" мономера говорит о том, что терминирующие кодоны
- мощность множества. Наличие в спектре значений дискретной функции (8.3) "пустого" мономера говорит о том, что терминирующие кодоны  -РНК можно идентифицировать только антикодонами
-РНК можно идентифицировать только антикодонами  -РНК, которые не "нагружены" аминокислотами.
-РНК, которые не "нагружены" аминокислотами.
Теперь вырожденность генетического кода можно представить отношением эквивалентности (эквизначности
), которое разбива-конечное множество 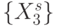 значений идентификационной активно-сти триплетов на непересекающиеся подмножества
значений идентификационной активно-сти триплетов на непересекающиеся подмножества 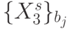 , такие, что
, такие, что 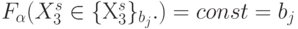 . В комбинаторике [90] отношение эквивалентности рассматривается как некоторое 1-разбиение конечного множества
. В комбинаторике [90] отношение эквивалентности рассматривается как некоторое 1-разбиение конечного множества 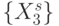 на эквизначные подмножества:
на эквизначные подмножества:
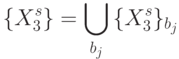
Здесь 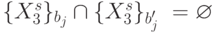 , если
, если 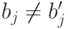 ;
;  - теоретико-множественное пересечение,
- теоретико-множественное пересечение,  - "пустое" множество, а
- "пустое" множество, а  - теоретико-множественное объединение.
- теоретико-множественное объединение.
Каждое  -разбиение характеризуется первичной
-разбиение характеризуется первичной 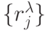 и вторичной
и вторичной 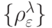 спецификациями
спецификациями
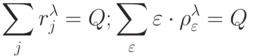
В параметрах табл. 8.1 элементы первичной спецификации 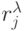 характеризуют вырожденность кода для каждой
характеризуют вырожденность кода для каждой 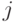 -й аминокислоты:
-й аминокислоты: 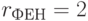 ;
;  ;
;  ;
; 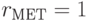 ;
; 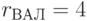 ;
; 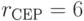 ;
; 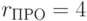 ;
; 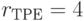 ;
; 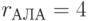 ;
; 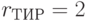 ;
; 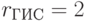 ;
; 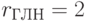 ;
;  ;
; 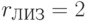 ;
; 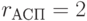 ;
; 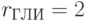 ;
;  ;
; 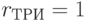 ;
; 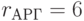 ;
; 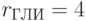 ;
; 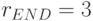 . Элементы вторичной спецификации говорят о том, сколько аминокислот имеет одинаковую вырожденность
. Элементы вторичной спецификации говорят о том, сколько аминокислот имеет одинаковую вырожденность 
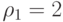 ;
;  ;
; 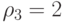 ;
; 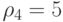 ;
; 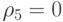 ;
; 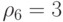 .
.
Общее количество таблиц вырожденности с такой первичной и вторичной спецификацией оценивается факториальным соотношением [90, 119] 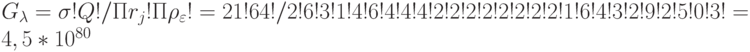 .
.
Синтез предбиологических макромолекул, к которым относится и ДНК, можно было осуществить только феноменологическими методами и средствами самоорганизации диссипативных гетероструктур [34]. Поэтому если бы на генерацию и анализ одной таблицы вырожденности типа таблица1 уходила только 1 секунда, то времени жизни Вселенной не хватило бы
на выбор оптимального варианта, так как за  лет с такой скоростью можно проанализировать только
лет с такой скоростью можно проанализировать только 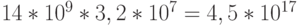 вариантов.
вариантов.
Отсюда: правила кодирования табл. 8.1 следует рассматривать как квазиоптимальные и, скорее всего, экспериментально проверенные только в условиях Земли. С учетом предбиологического этапа эволюции [231] оптимальный в некотором смысле отбор триплетных таблиц вырожденности экосистемы Земли, построенной не более чем из 20 типов аминокислот, согласно проведенной формализации требует генерации и анализа 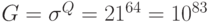 вариантов.
вариантов.
Таким образом, эволюционный отбор таблицы вырожденности генетического кода имеет четко выраженный перечислительный характер, и поэтому его достаточно просто свести к классической задаче комбинаторного анализа с помощью одного формального определения идентификационной активности элементарной молекулярно-биологической структуры.
Проведенная формализация позволяет получить многопороговую модель биологического кода, которая является частным случаем классической многопороговой модели:
![(l_{s}(X^s_n,W_{n})= \sum_{i=1}^{n}{x_i^s w_i)\in (h_{j-1},h_j]\Rightarrow f_s:=b_j,](/sites/default/files/tex_cache/1f577b84084ecb93dd52a0cbd0773032.png) |
( 8.4) |
если ее настроить на реализацию функции (8.3). (Здесь сохранены условные обозначения раздела 4.5.)
Для этого необходимо [78, 80]:
- Зафиксировать параметры входных сигналов модели согласно (8.1), а выходного сигнала - согласно табл. 8.1.
- Выбрать критерий оптимальности, в качестве которого обычно используют оценку структурной сложности модели
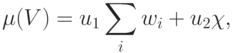
где
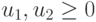 - некоторые одновременно неравные нулю коэффициенты, характеризующие "стоимость" реализации "единицы веса" и "единицы порога", а
- некоторые одновременно неравные нулю коэффициенты, характеризующие "стоимость" реализации "единицы веса" и "единицы порога", а 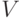 - многопороговая модель (см. раздел 4.6).
- многопороговая модель (см. раздел 4.6). - Найти "весовой" вектор
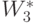 , удовлетворяющий критерию:
, удовлетворяющий критерию: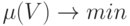
( 8.5)
В цифроаналоговой технике входное преобразование (много)поро-говой модели выполняется относительно "простыми" усилителями с варьируемыми коэффициентами усиления ( 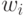 ), а разбиения - достаточно "сложными" компараторами. Поэтому
), а разбиения - достаточно "сложными" компараторами. Поэтому 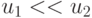 и
и 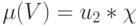 . В таком операционном базисе разработчики стремятся к минимально пороговой реализации, что требует поиска "весового" вектора
. В таком операционном базисе разработчики стремятся к минимально пороговой реализации, что требует поиска "весового" вектора 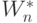 , обеспечивающего представление дискретной функции
, обеспечивающего представление дискретной функции 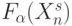 на скалярной оси
на скалярной оси  , близкое монотонно эквизначному В случае функции (8.3) критерий (8.5) удовлетворяется, если
, близкое монотонно эквизначному В случае функции (8.3) критерий (8.5) удовлетворяется, если 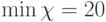 . В цифровой технике входное преобразование (много)пороговой модели требует
. В цифровой технике входное преобразование (много)пороговой модели требует  аппаратных умножителей, которые гораздо "сложнее" компараторов, то есть
аппаратных умножителей, которые гораздо "сложнее" компараторов, то есть 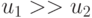 . Поэтому здесь уже не требуется монотонно эквизначные представление
. Поэтому здесь уже не требуется монотонно эквизначные представление  , и варьируемым становится не столько "весовой" вектор
, и варьируемым становится не столько "весовой" вектор  , сколько пороговый
, сколько пороговый 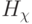 как по значениям компонентов
как по значениям компонентов 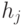 , так и по их количеству
, так и по их количеству 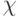 .
.
Подразумевая 2-й вариант реализации (много)пороговой модели, компоненты "весового" вектора 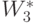 выберем исходя из условия взаимно однозначного соответствия
выберем исходя из условия взаимно однозначного соответствия 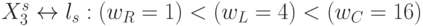 .
.
Тогда формальные кодоны 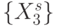 биологического кода упорядочиваются по возрастанию взвешенной идентификационной активности
биологического кода упорядочиваются по возрастанию взвешенной идентификационной активности 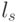 , как показано в табл. 8.2, а размерность вектора порогов
, как показано в табл. 8.2, а размерность вектора порогов  отличается от минимальной всего на 4 единицы. Это отклонение вызвано нарушением монотонно эквизначного представления функции (8.3) на скалярной оси
отличается от минимальной всего на 4 единицы. Это отклонение вызвано нарушением монотонно эквизначного представления функции (8.3) на скалярной оси  для значений взвешенной идентификационной активности, отвечающей аминокислотам
для значений взвешенной идентификационной активности, отвечающей аминокислотам 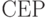 ,
,  и
и  , а также одной "пустой" аминокислоте
, а также одной "пустой" аминокислоте  , которая в реальных молекулярно-биологических комплексах "используется" как признак конца полимеризации.
, которая в реальных молекулярно-биологических комплексах "используется" как признак конца полимеризации.
Фактическое отклонение от минимально пороговой реализации гораздо больше (  - дополнительные пороги в табл. 8.2 показаны пунктирными линиями), так как реальный молекулярно-биологический базис синтеза нативных белков образуют процедуры взаимной структурно-параметрической идентификации (узнавания) [230]:
- дополнительные пороги в табл. 8.2 показаны пунктирными линиями), так как реальный молекулярно-биологический базис синтеза нативных белков образуют процедуры взаимной структурно-параметрической идентификации (узнавания) [230]:
-
 -РНК и аминокислоты во время образования комплекса "аминоа-цил -
-РНК и аминокислоты во время образования комплекса "аминоа-цил -  -РНК";
-РНК"; - инициированного рибосомой кодона
 -РНК и антикодона в составе комплекса "аминоацил -
-РНК и антикодона в составе комплекса "аминоацил -  -РНК" во время трансляции биологического кода в "аминокислотный формат".
-РНК" во время трансляции биологического кода в "аминокислотный формат".

![Обобщенная вторичная структура транспортных РНК [233]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/8/files/08_02.gif)