Классы

Конструкторы класса Rational

Инициализация полей конструктором по умолчанию никак не может нас устраивать, поскольку нулевой знаменатель - это нонсенс. Поэтому определим конструктор с аргументами, которому будут передаваться два целых: числитель и знаменатель создаваемого числа. Кажется, что это единственный разумный конструктор, который может понадобиться нашему классу. Однако чуть позже мы добавим в класс закрытый конструктор и статический конструктор, позволяющий создать константы нашего класса. Вот определение конструктора:

/// <summary>
/// Конструктор класса. Создает рациональное число
/// m/n, эквивалентное a/b, но со взаимно несократимыми
/// числителем и знаменателем. Если b=0, то результатом
/// является рациональное число 0 -пара (0,1).
/// </summary>
/// <param name="a">числитель</param>
/// <param name="b">знаменатель</param>
public Rational(int a, int b)
{
	if(b==0) {m=0; n=1;}
	else
	{
		//приведение знака
		if( b<0) {b=-b; a=-a;}
		//приведение к несократимой дроби
		int d = nod(a,b);
		m=a/d; n=b/d;
	}
}

Как видите, конструктор класса может быть довольно сложным.

В нем, как в нашем случае, может проверяться корректность задаваемых аргументов. Для рациональных чисел мы полагаем, что задание нулевого знаменателя означает задание рационального числа 0, и это эквивалентно заданию пары (0, 1). В остальных случаях выполняется приведение заданной пары чисел к эквивалентному рациональному числу с несократимыми числителем и знаменателем. По ходу дела вызывается закрытый метод класса, вычисляющий значение НОД(a,b) - наибольшего общего делителя чисел a и b.

Методы класса Rational

Если поля класса почти всегда закрываются, чтобы скрыть от пользователя представление данных класса, то методы класса всегда имеют открытую часть - те сервисы (службы), которые класс предоставляет своим клиентам и наследникам. Но не все методы открываются. Большая часть методов класса может быть закрытой, скрывая от клиентов детали реализации, необходимые для внутреннего использования. Заметьте, сокрытие представления и реализации делается не по соображениям утаивания того, как реализована система. Чаще всего, ничто не мешает клиентам ознакомиться с полным текстом класса. Сокрытие делается в интересах самих клиентов. При сопровождении программной системы изменения в ней неизбежны. Клиенты не почувствуют на себе негативные последствия изменений, если они делаются в закрытой части класса. Чем больше закрытая часть класса, тем меньше влияние изменений на клиентов класса.

Закрытый метод НОД

Метод, вычисляющий наибольший общий делитель пары чисел, понадобится не только конструктору класса, но и всем операциям над рациональными числами. Алгоритм нахождения общего делителя хорошо известен со времен Эвклида. Я приведу программный код метода без особых пояснений:

/// <summary>
/// Закрытый метод класса.
/// Возвращает наибольший общий делитель чисел a,b
/// </summary>
/// <param name="a">первое число</param>
/// <param name="b">второе число, положительное</param>
/// <returns>НОД(a,b)</returns>
int nod(int m, int n)
{
	int p=0;
	m=Math.Abs(m); n =Math.Abs(n);
	if(n>m){p=m; m=n; n=p;}
	do
	{
	p = m%n; m=n; n=p;
	}while (n!=0);
	return(m);
}//nod

Печать рациональных чисел

Почти любой класс содержит один или несколько методов, позволяющих выводить на печать данные о классе. Такой метод имеется и в классе Rational. Вот его текст:

public void PrintRational(string name)
{
	Console.WriteLine(" {0} = {1}/{2}",name,m,n);
}

Метод печатает имя и значение рационального числа в форме m/n.

Тестирование создания рациональных чисел

В классе Testing, предназначенном для тестирования нашей работы и являющегося клиентом класса Rational, создадим процедуру, позволяющую проверить корректность создания рациональных чисел. Вот эта процедура:

public void TestCreateRational()
{
	Rational r1=new Rational(0,0), r2 = new Rational(1,1);
	Rational r3=new Rational(10,8), r4 = new Rational(2,6);
	Rational r5=new Rational(4,-12), r6 = new Rational (-12,-14);
	r1.PrintRational("r1:(0,0)"); 
	r2.PrintRational("r2:(1,1)");
	r3.PrintRational("r3:(10,8)");
	r4.PrintRational("r4:(2,6)");
	r5.PrintRational("r5: (4,-12)"); 
	r6.PrintRational("r6: (-12,-14)");
}

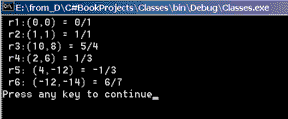
Она создает и печатает шесть рациональных чисел. Вот как выглядят результаты ее работы.

Рис. 16.3. Создание и печать рациональных чисел