|
Постройте таблицу значений функции |
Реализация циклического алгоритма
Занятие 2. Исследование таблицы значений функции
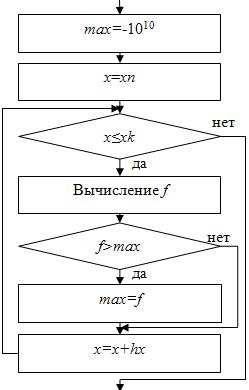
Существуют специальные приемы для нахождения некоторых величин, таких как наибольшее (наименьшее) значение функции, сумма значений функции, произведение значений функции, среднее арифметическое значений функции, количество значений функции.
- Нахождение наибольшего
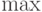 (наименьшего
(наименьшего  ) значения функции.
Примечание. Если нужно найти наименьшее значение функции, то следует сделать следующие замены: "
) значения функции.
Примечание. Если нужно найти наименьшее значение функции, то следует сделать следующие замены: "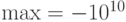 " поменять на "
" поменять на "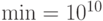 ", "
", "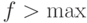 " поменять на "
" поменять на "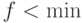 ", "
", "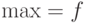 " поменять на "
" поменять на "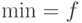 ".
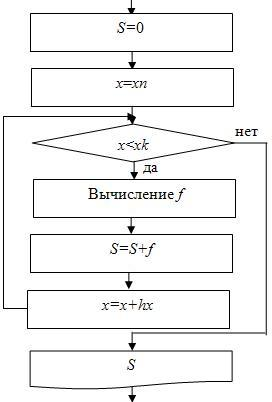
". - Нахождение суммы
 значений функции
значений функции
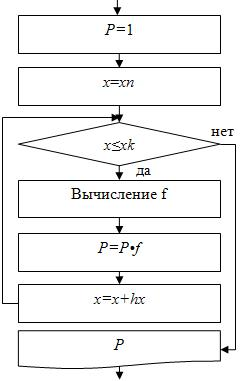
- Нахождение произведения
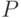 значений функции
значений функции
- Нахождение среднего арифметического значения
 и количества
и количества  значений функции
значений функции
Пример 4. Вычислить таблицу "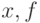 " значений функции
" значений функции 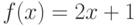 при
при 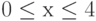 с шагом 1. Найти сумму всех значений функции; произведение значений, меньших 6; минимальное значение функции.
с шагом 1. Найти сумму всех значений функции; произведение значений, меньших 6; минимальное значение функции.
Решение. Расчет значений функции, вывод таблицы значений на экран, а также нахождение всех необходимых величин реализуется в цикле по  . Поэтому в данной задаче будет организован один цикл по
. Поэтому в данной задаче будет организован один цикл по  , в теле цикла будем рассчитывать функцию, выводить на экран строку таблицы, насчитывать сумму, произведение, минимальное значение функции.
, в теле цикла будем рассчитывать функцию, выводить на экран строку таблицы, насчитывать сумму, произведение, минимальное значение функции.
Введем обозначения:
-
 – сумма всех значений функции,
– сумма всех значений функции, -
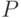 – произведение значений, меньших 6,
– произведение значений, меньших 6, -
 – минимальное значение функции.
– минимальное значение функции.
Т.к. нужно найти произведение значений, меньших 6, то следует добавить условие " " при вычислении произведения.
" при вычислении произведения.
Будем реализовывать цикл с предусловием, используя оператор for.
| Блок-схема с предусловием: | Код программы с оператором for: |
// proga26.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
double x,f,S,P,min;
cout<<setw(10)<<"x"<<setw(10)<<"f"<<endl;
S=0;
P=1;
min=10E10;
for(x=0; x<=4; x=x+1){
f=2*x+1;
cout<<setw(10)<<x<<setw(10)<<f<<endl;
S=S+f;
if(f<6){
P=P*f;
}
if(f<min){
min=f;
}
}
cout<<"S="<<S<<endl;
cout<<"P="<<P<<endl;
cout<<"min="<<min<<endl;
return 0;
} |
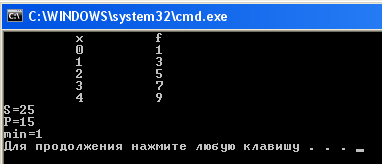
Результат выполнения программы:
Ручной счет:
Диапазон значений х: 0, 1, 2, 3, 4. при x=0 f=2x+1=2*0+1=1; при x=1 f=2x+1=2*1+1=3; при x=2 f=2x+1=2*2+1=5; при x=3 f=2x+1=2*3+1=7; при x=4 f=2x+1=2*4+1=9; сумма всех значений:S=1+3+5+7+9=25; произведение значений, меньших 6: P=1*3*5=15; наименьшее значение функции: min=1.
Примечание. Если функция зависит от двух переменных, то следует реализовывать двумерный цикл, причем тело внутреннего цикла будет организовано так же, как в данном примере.
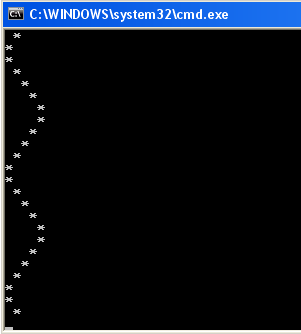
Пример 5. Нарисовать на экране бесконечную "змейку" символами "*".
Решение. Определим сначала внешний вид "змейки":
* * * * * * * * *
Т.к. "змейка" должна быть бесконечной, то необходимо организовать бесконечный цикл. В этом случае будем использовать оператор while с всегда выполняемым условием true: while(true). Внутри этого бесконечного цикла будем рисовать один период "змейки", т.е. один холм. За счет бесконечного цикла на экране будет бесконечное число раз рисоваться наш холм.
Теперь стоит решить, какой ширины будет наша "змейка". Будем запрашивать ширину "змейки" у пользователя, т.е. с клавиатуры. Обозначим ширину переменной  . Холм состоит из двух частей – расширяющейся и сужающейся. Чтобы нарисовать расширяющуюся часть, будем использовать цикл for по переменной
. Холм состоит из двух частей – расширяющейся и сужающейся. Чтобы нарисовать расширяющуюся часть, будем использовать цикл for по переменной  от 1 до
от 1 до  и функцию setw(i). Чтобы нарисовать сужающуюся часть, будем использовать цикл for по переменной
и функцию setw(i). Чтобы нарисовать сужающуюся часть, будем использовать цикл for по переменной  от
от  до 1 и функцию setw(i).
до 1 и функцию setw(i).
Таким образом, внутри бесконечного цикла while вложены последовательно два цикла for – первый с увеличением переменной цикла, второй с уменьшением.
Код программы:
// snake.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
int i, n;
cout<<"vvedi n=";
cin>>n;
while (true){
for(i=1; i<=n; i=i+1){
cout<<setw(i)<<"*"<<endl;
}
for(i=n; i>=1; i=i-1){
cout<<setw(i)<<"*"<<endl;
}
}
return 0;
}Результат выполнения программы: при 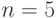 :
:
Краткие итоги
В любой задаче, где встречается повторение действий, необходимо использовать циклический алгоритм. От выбора оператора цикла результат не должен зависеть. Принципы вычислений таких величин, как сумма, произведение и т.д., использует циклический алгоритм в своей основе.
Упражнения
- Составьте блок-схему и программу для вычисления суммы всех целых чисел от 1 до 100 включительно.
- Постройте таблицу значений функции
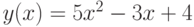 при
при  с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается. - Составьте блок-схему и программу для вычисления таблицы значений функций
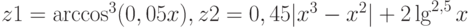 при
при 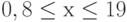 c шагом 1. Найдите сумму всех значений
c шагом 1. Найдите сумму всех значений 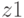 , количество значений
, количество значений 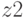 , меньших 10, наимешьшее значение
, меньших 10, наимешьшее значение 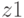 , наибольшее значение
, наибольшее значение 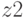 .
. - Составьте блок-схему и программу для вычисления таблицы значений функции
![Z(x,y)=\begin{cases}\sin^{0.4}(x^{4y})+\lg\sqrt{y-\frac{x}{y-0.8}},&\text{если}\ x+y<-2\\2.3,&\text{если}\ -2\le x+y\le 0\\\frac{\sqrt[3]{x}-\sqrt[3]{y}}{x}-y,&\text{если}\ x+y>0\end{cases}](/sites/default/files/tex_cache/ebd9625ef500050b498c5db39e8eb700.png) при
при 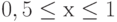 c шагом 0,05; y задать с клавиатуры.
c шагом 0,05; y задать с клавиатуры. - Составьте блок-схему и программу для вычисления таблицы значений функции
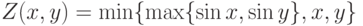 при
при 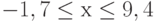 c шагом 9,3;
c шагом 9,3; 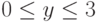 c шагом 0,75. Определите наибольшее отрицательное значение функции, наименьшее положительное значение функции, произведение ненулевых значений функции, количество значений функции, больших 1 или меньших -1.
c шагом 0,75. Определите наибольшее отрицательное значение функции, наименьшее положительное значение функции, произведение ненулевых значений функции, количество значений функции, больших 1 или меньших -1. - Составьте программу, которая нарисует на экране геометрическую фигуру. Попробуйте разные варианты:
- квадрат,
- треугольник,
- прямоугольник.



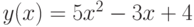 при
при 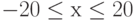 с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается.