Алгоритмы асимметричного шифрования
Криптография с использованием эллиптических кривых
Математические понятия
Преимущество подхода на основе эллиптических кривых в сравнении с задачей факторизации числа, используемой в RSA, или задачей целочисленного логарифмирования, применяемой в алгоритме Диффи-Хеллмана и в DSS, заключается в том, что в данном случае обеспечивается эквивалент-ная защита при меньшей длине ключа.
В общем случае уравнение эллиптической кривой Е имеет вид:
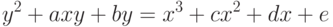
В качестве примера рассмотрим эллиптическую кривую Е, уравнение которой имеет вид:
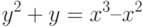
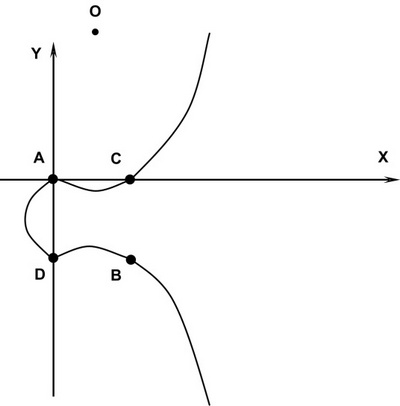
На этой кривой лежат только четыре точки, координаты которых являются целыми числами. Это точки
А (0, 0), В (1, -1), С (1, 0) и D (0, -1)
Для определения операции сложения двух точек на эллиптической кривой сделаем следующие предположения:
- На плоскости существует бесконечно удаленная точка О принадлежит Е, в которой сходятся все вертикальные прямые.
- Будем считать, что касательная к кривой проходит через точку касания два раза.
- Если три точки эллиптической кривой лежат на прямой линии, то их сумма есть О.
Введем следующие правила сложения точек на эллиптической кривой:
- Точка О выступает в роли нулевого элемента. Так, О = –О, и для любой точки Р на эллиптической кривой Р + О = Р.
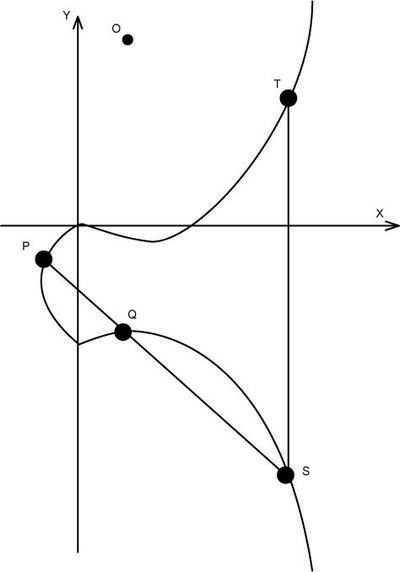
- Вертикальная линия пересекает кривую в двух точках с одной и той же координатой х S=(x,y) и T=(x,-y). Эта прямая пересекает кривую и в бесконечно удаленной точке. Поэтому Р1 + Р2+ О = О и Р1 = –Р2.
- Чтобы сложить две точки P и Q с разными координатами х, следует провести через эти точки прямую и найти точку пересечения ее с эллиптической кривой. Если прямая не является касательной к кривой в точках P или Q, то существует только одна такая точка, обозначим ее S. Согласно нашему предположению
P + Q + S = О
Следовательно,
P + Q = –S или
P + Q = T
Если прямая является касательной к кривой в какой-либо из точек P или Q, то в этом случае следует положить S=P или S=Q соответственно.
Чтобы удвоить точку Q, следует провести касательную в точке Q и найти другую точку пересечения S с эллиптической кривой. Тогда Q + Q = 2?Q = -S.
Введенная таким образом операция сложения подчиняется всем обычным правилам сложения, в частности коммутативному и ассоциативному законам. Умножение точки Р эллиптической кривой на положительное число k определяется как сумма k точек Р.
В криптографии с использованием эллиптических кривых все значения вычисляются по модулю р, где р является простым числом. Элементами данной эллиптической кривой являются пары неотрицательных целых чисел, которые меньше р и удовлетворяют частному виду эллиптической кривой:
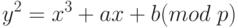
Такую кривую будем обозначать Ep(a,b). При этом числа а и b должны быть меньше р и должны удовлетворять условию 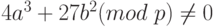 . Множество точек на эллиптической кривой вычисляется следующим образом.
. Множество точек на эллиптической кривой вычисляется следующим образом.
Для каждого такого значения х, что 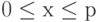 , вычисляется
, вычисляется 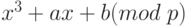 .
.
Для каждого из полученных таким образом значений выясняется, имеет ли это значение целочисленный квадратный корень. Если нет, то в Ep (a,b) нет точек с этим значением х. Если целочисленный корень существует, имеется два значения y, равные этим значениям квадратного корня. Исключением является случай, когда y равен нулю. Эти значения (x,y) и будут точками Ep(a,b).
Алгоритм цифровой подписи на основе эллиптических кривых ECDSA
Создание ключей:
Выбирается эллиптическая кривая Ep(a,b). Число точек на ней должно делиться на большое целое n.
Выбирается точка Р ∈ Ep(a,b).
Выбирается случайное число d ∈ [1,n-1].
Вычисляется Q = d×P.
Закрытым ключом является d, открытым ключом (E, P, n, Q).
Создание подписи:
Выбирается случайное число k ∈ [1,n-1].
Вычисляется k×P = (x1, y1) и r = x1 (mod n). Проверяется, чтобы r не было равно нулю, так как в этом случае подпись не будет зависеть от закрытого ключа. Если r = 0, то выбирается другое случайное число k.
Вычисляется

Вычисляется
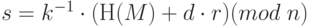
Проверяется, чтобы s не было равно нулю, так как в этом случае необходимого для проверки подписи числа s-1(mod n) не существует. Если s=0, то выбирается другое случайное число k.
Подписью для сообщения М является пара чисел (r,s).
Проверка подписи:
Проверяется, что целые числа r и s принадлежат диапазону чисел [0,n-1]. В противном случае результат проверки отрицательный, и подпись отвергается.
Вычисляется
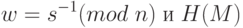
Вычисляется
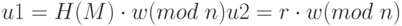
Вычисляется
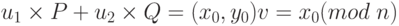
Подпись верна в том и только том случае, когда v = r.